геометрия 2 задачи. Площадь
 Скачать 337.97 Kb. Скачать 337.97 Kb.
|
§6. Анализ задач ОГЭ по теме «Площадь многоугольника» в курсе геометрии основной школы.В основном государственном экзамене встречаются задания, где необходимо вычислить площади фигур, которые изображены на клетчатой бумаге. В основном такие задачи даются для учащихся довольно просто, если эта фигура представлена в виде треугольника, параллелограмма или трапеции. Нужно всего лишь знать по какой формуле вычисляются эти площади фигур. Для вычисления достаточно сосчитать количество этих точек. Однако, фигуры могут быть нам даны в виде произвольного многоугольника. Для решения таких задач, нам необходимо использовать особые методы. Разберемся в особенностях таких задач. Оказывается, есть такая универсальная особая формула, с помощью которой мы можем вычислить изображенную на клетке площадь фигуры. Она называется формулой Пика. Особенность этой формулы заключается в простоте получении результата и ее применении, но в школьном курсе геометрии эту формулу не рассматривают. На рассмотрение возьмем многоугольник, имеющий целочисленные координаты. Узлами называют точки с целочисленными координатами. Допустим. Мы должны найти его площадь. Фигура может представлять собой трапецию, параллелограмм, треугольник. Нужно найти диагонали, высоту и стороны, подсчитав клетки. Полученные величины подставить в формулу для нахождения площади. К примеру, нам дан рисунок 1. Размер клетки 1 см на 1 см.    Решение: Подсчитав клетки, найдем: а = 6см, h = 3см. С помощью формулы получим: S = ∙ Решение: Подсчитав клетки, найдем: а = 6см, h = 3см. С помощью формулы получим: S = ∙      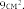 a ∙ h = a ∙ h =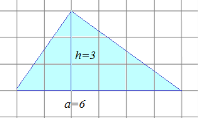 Рис.1. Треугольник Фигура представлена многоугольником. Фигура, представленная в виде многоугольника, дает возможность пользоваться следующими методами. Метод разбиения: Нахождение суммы всех площадей фигур; Нахождение площади, получившихся фигур; Разбиение многоугольника на треугольники и прямоугольники. 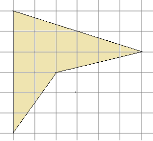 Для примера, методом разбиения нам необходимо вычислить площадь фигуры, которая изображена с размером клетки 1 см на 1 см на рисунке 2. Для примера, методом разбиения нам необходимо вычислить площадь фигуры, которая изображена с размером клетки 1 см на 1 см на рисунке 2.Решение. Существует большое количество способов разбиения. Для упрощения задачи мы можем разбить фигуру на прямоугольник и прямоугольные треугольники, показанные на рисунке 3.       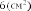 S2 = , S3 =              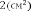  Сложив площади всевозможных фигур, получаем: S = 6 + 2 + 2 + 3 = 13( Сложив площади всевозможных фигур, получаем: S = 6 + 2 + 2 + 3 = 13(Рис.2. Многоугольник 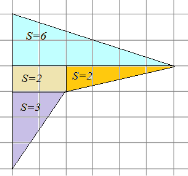 Рис.3. Метод  разбиения разбиенияМетод дополнительного построения: До самого прямоугольника достроить фигуру; Найти площадь прямоугольника и площадь, полученную дополнительными фигурами; От самой площади прямоугольника отнять площади всех оставшихся фигур. В качестве примера, при помощи метода дополнительного построения нам потребуется вычислить площадь многоугольника, которая изображена с размером клетки 1см на 1 см на рисунке 2. 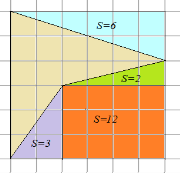 Решение: Необходимо достроить данную фигуру до самого прямоугольника, на рисунке 4. Решение: Необходимо достроить данную фигуру до самого прямоугольника, на рисунке 4.Рис.4. Метод дополнения многоугольника У большого прямоугольника площадь будет равна: Sб.пр. = 6 ∙ 6 = 36 см2.    Внутренний прямоугольник: Sпр. = 3 ∙ 4 = 12см2. Площадь оставшихся треугольников: S1 = ∙6 ∙ 2 = Внутренний прямоугольник: Sпр. = 3 ∙ 4 = 12см2. Площадь оставшихся треугольников: S1 = ∙6 ∙ 2 =     6см2, S2 = =2см2, 6см2, S2 = =2см2,      S3 = см2. S3 = см2.Рис.4. Метод дополнения Площадь искомой фигуры будет равна: S = 36 – 12 – 6 – 2 – 3 = 13см2. Также мы еще имеем право использовать метод, являющихся формулой Пика. Покажем ее на примере: Нам дан многоугольник, имеющий только целочисленные вершины. Узлами решетки мы считаем точки, обе координаты которых целые. Многоугольник может являться и выпуклым и невыпуклым.      Площадь многоугольника, данная с целочисленными вершинами будет равна: S = B + Г – целочисленное точки, находящиеся на границе Площадь многоугольника, данная с целочисленными вершинами будет равна: S = B + Г – целочисленное точки, находящиеся на границемногоугольника. 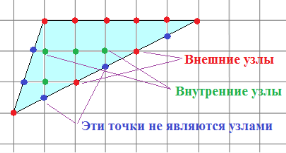 К примеру, на изображенном рисунке 5 многоугольника. К примеру, на изображенном рисунке 5 многоугольника.В качестве примера нам дан рисунок 2, размер клетки 1см на 1 см. По формуле Пика нам нужно вычислить площадь фигуры. Рис.5. Узлы формулы Пика Решение: Ориентируясь на рисунок 6, В = 9, Г =   Используя формулу Пика: S = 9 + – 1 = 13см2. Используя формулу Пика: S = 9 + – 1 = 13см2.Для вычисления площадей формула Пика является универсальной, она применима к любой фигуре. Но есть большая вероятность допустить ошибку в подсчетах узлов решетки, если многоугольник 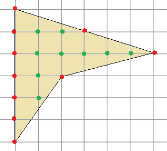 Рис.6. Многоугольник. Формула Пика занимает большую площадь. Исследуя подобные задачи ОГЭ, можно сделать вывод, что лучше пользоваться традиционными методами (дополнение или разбиение), а сам результат проверить с помощью формулы Пика. Методическая система, включающая в себя планиметрические задачи по теме «Площадь многоугольника», ориентированная на формирование у школьников умений и навыков, применять теоретические знания к решению задач На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.7). Найти площадь данного многоугольника. На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.1). Найти площадь данного многоугольника. На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.9). Найти площадь данного многоугольника. 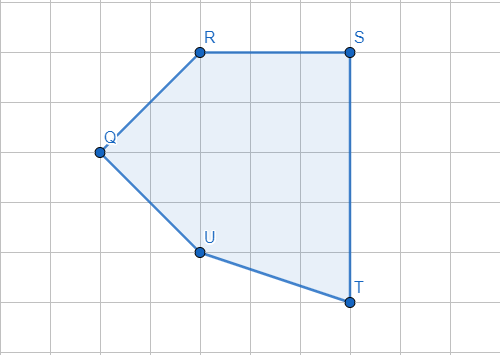 На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.10). Найти площадь данного многоугольника. На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.10). Найти площадь данного многоугольника.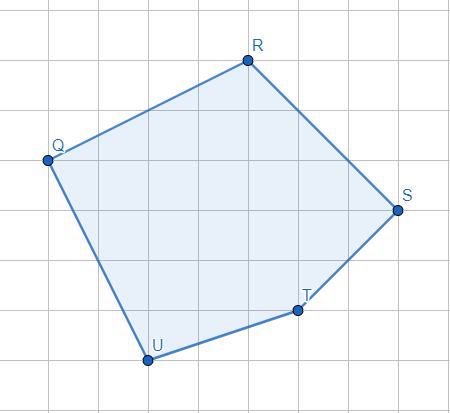 Рис.7. Многоугольник на клетчатой бумаге 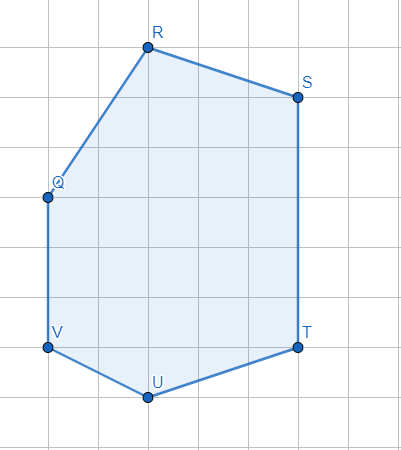 Рис.8. Многоугольник на клетчатой бумаге 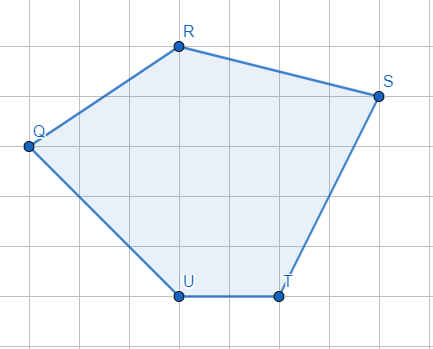 Рис.9. Многоугольник на клетчатой бумаге Рис.10. Многоугольник на 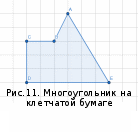 На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.11). Найти площадь данного многоугольника. На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.11). Найти площадь данного многоугольника. На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.12). Найти площадь данного многоугольника. На клетчатой бумаге с размером клетки 4×4 задан многоугольник (Рис.12). Найти площадь данного многоугольника.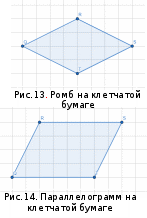 На клетчатой бумаге с размерами клетки 4×4 задан ромб QRST (Рис.13). Найти На клетчатой бумаге с размерами клетки 4×4 задан ромб QRST (Рис.13). Найтиплощадь ромба; длины диагоналей ромба; тангенс его острого угла; тангенс его тупого угла; радиус окружности, вписанной в ромб. На клетчатой бумаге с размерами клетки 4×4 задан 33 параллелограмм QRST (Рис. 14). Найти площадь параллелограмма; длину диагонали QS; длину диагонали RT; тангенс ∠RST; синус ∠RQT; косинус ∠QTS; синус угла между его диагоналями. 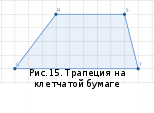 На клетчатой бумаге с размерами клетки 4×4 задана трапеция QRST (Рис. 15). Найти На клетчатой бумаге с размерами клетки 4×4 задана трапеция QRST (Рис. 15). Найтиплощадь трапеции; среднюю линию трапеции; длины боковых сторон трапеции; косинусы тупых углов трапеции; косинусы острых углов трапеции. Задача №1. Найти площадь равностороннего треугольника со стороной равной стороне квадрата, площадь которого равна 16. Дано: квадрат; Площадь квадрата равна 16; Правильный треугольник; Сторона треугольника равна стороне квадрата. Найти: Площадь треугольника.  Решение. Так как площадь данного квадрата равна 16, то длина его стороны равна 4. Здесь учащимся необходимо напомнить, что площадь Решение. Так как площадь данного квадрата равна 16, то длина его стороны равна 4. Здесь учащимся необходимо напомнить, что площадь   правильного треугольника со стороной авычисляется по формуле . правильного треугольника со стороной авычисляется по формуле .     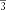 Согласно этой формуле получаем, что . Согласно этой формуле получаем, что . 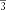 Ответ: . Ответ: . 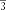 Задача №2. Найти площадь квадрата со стороной равной стороне правильного треугольника площади . Задача №2. Найти площадь квадрата со стороной равной стороне правильного треугольника площади .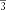 Дано: правильный треугольник; Площадь треугольника равна ; Дано: правильный треугольник; Площадь треугольника равна ;Сторона квадрата равна стороне треугольника. Найти: Площадь квадрата.   Решение. Учащимся необходимо обратить внимание на тот факт, что эта задача взаимосвязана с предыдущей. Поскольку в ней известна площадь правильного треугольника, а найти следует площадь квадрата. Используем известную формулу для вычисления площади правильного треугольника Решение. Учащимся необходимо обратить внимание на тот факт, что эта задача взаимосвязана с предыдущей. Поскольку в ней известна площадь правильного треугольника, а найти следует площадь квадрата. Используем известную формулу для вычисления площади правильного треугольника        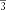 . Составляем уравнение . Откуда находим, что . Составляем уравнение . Откуда находим, что Поскольку площадь квадрата равна квадрату длины его стороны, значит, она равна 100. Ответ: 100. Задача №3. Найти площадь квадрата со стороной равной диагонали прямоугольника со сторонами 3 см. и 4 см. Дано: прямоугольник; Стороны прямоугольника равны 3см. и 4 см. Квадрат; Сторона квадрата равна стороне треугольника. Найти: Площадь квадрата. Решение: Обозначим заданный прямоугольник через ABCD. Пусть АВ=3см, а CD=4см. Важно обратить внимание учащихся на тот факт, что     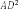 треугольник ADC является прямоугольным. Значит, к нему можно применить теорему Пифагора. Следовательно, треугольник ADC является прямоугольным. Значит, к нему можно применить теорему Пифагора. Следовательно,  квадрата будет равна квадрату диагонали. Таким образом, получаем, что площадь квадрата равна 25. Ответ: 25. Задача №4. Найти сторону квадрата, зная, что он равновелик с параллелограммом, боковая сторона которого равна 5см, а высота, проведенная к этой стороне равна 6 см. Дано: параллелограмм АBCD; АВ=5см, DH= 6 см. ; Квадрат; Площадь квадрата равна площади параллелограмма; Найти: сторону квадрата.   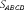 Решение. В начале решения этой задачи необходимо вспомнить совместно с учениками формулу для вычисления площади параллелограмма. Важно отметить, что эта формула справедлива как в случае, когда основанием служит сторона AD, так и в случае, когда основанием служит боковая сторона АВ. Согласно этой формуле получаем, что Решение. В начале решения этой задачи необходимо вспомнить совместно с учениками формулу для вычисления площади параллелограмма. Важно отметить, что эта формула справедлива как в случае, когда основанием служит сторона AD, так и в случае, когда основанием служит боковая сторона АВ. Согласно этой формуле получаем, что    . Так как площадь квадрата с одной стороны равна площади параллелограмма, а с другой стороны квадрату его стороны, значит, сторона квадрата равна . . Так как площадь квадрата с одной стороны равна площади параллелограмма, а с другой стороны квадрату его стороны, значит, сторона квадрата равна . Ответ: . Ответ: .Задача №5. Найти сторону квадрата, зная, что он равновелик с трапецией, диагонали которой равны 15 см и 12 см, а угол между ними равен Дано: трапеция АBCD;  АС=15см, ВD= 12 см. , АС=15см, ВD= 12 см. , Квадрат ; Площадь квадрата равна площади трапеции ABCD; Найти: сторону квадрата. Решение. Важно обратить внимание учащихся на тот факт, что для вычисления площади трапеции можно использовать различные формулы и способы. В данном случае трапеция задана диагоналями и углом между ними, поэтому для нее можно использовать более общую формулу, которую обычно используют для вычисления площади четырехугольника. Здесь важное значение приобретает тот факт, что трапеция это есть частный случай четырехугольника. Таким образом, получаем, что      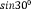         Ответ: Ответ: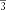 Задача №6. Найти сторону правильного треугольника, зная, что его площадь численно равна площади параллелограмма ABCD с диагоналями AC= см и BD=22 см и углом между ними Задача №6. Найти сторону правильного треугольника, зная, что его площадь численно равна площади параллелограмма ABCD с диагоналями AC= см и BD=22 см и углом между ними Дано: параллелограмм АBCD; 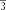 АС= см, ВD= 22 см. , АС= см, ВD= 22 см. , Правильный треугольник ; Площадь правильного треугольника равна площади параллелограмма ABCD; Найти: сторону треугольника.  Решение. Обычно учащиеся правильно решившие предыдущую задачу и хорошо усвоившие ход ее решения быстро ориентируются в том, что параллелограмм это тоже частный случай четырехугольника. Поэтому для вычисления его площади можно использовать более общую формулу, а именно ту, которую мы использовали при решении предыдущей задачи. Ценность задач подобного рода состоит в том, что при их решении учащиеся обнаруживают общие видовые сходства и отличия. Таким образом, получаем, что: Решение. Обычно учащиеся правильно решившие предыдущую задачу и хорошо усвоившие ход ее решения быстро ориентируются в том, что параллелограмм это тоже частный случай четырехугольника. Поэтому для вычисления его площади можно использовать более общую формулу, а именно ту, которую мы использовали при решении предыдущей задачи. Ценность задач подобного рода состоит в том, что при их решении учащиеся обнаруживают общие видовые сходства и отличия. Таким образом, получаем, что:      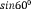        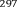 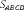    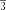 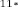 . . 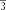 Поскольку по условию задачи с одной стороны площадь правильного треугольника со стороной х равна площади трапеции, а с другой стороны вычисляется по формуле Поскольку по условию задачи с одной стороны площадь правильного треугольника со стороной х равна площади трапеции, а с другой стороны вычисляется по формуле  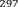   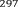        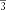 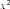 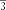 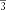 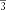        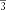  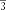  Откуда следует, что . Ответ: . Откуда следует, что . Ответ: .В качестве домашнего задания можно предложить учащимся следующие задачи. Найти сторону квадрата, зная, что его площадь численно равна площади ромба ABCD с диагоналями AC=24 см и BD=0,36 м. Найти сторону правильного треугольника, зная, что его площадь численно равна площади прямоугольника ABCD со сторонами АВ=27 см, ВС= 15 см.  Найти площадь квадрата, зная, что его сторона равна стороне правильного треугольника с высотой . Найти площадь квадрата, зная, что его сторона равна стороне правильного треугольника с высотой .Выводы по второй главе. Раскрыты формы, методы и средства обучения по решению планиметрических задач. Рассмотрены методические рекомендации по обучению темы «Площадь многоугольника». Разработана система задач ОГЭ по теме «Площадь многоугольника». |
