Пример 1
По семи территориям Уральского района за 199Х г. известны значения двух признаков (табл. 1.1).
Таблица 1.1
Район
|
Расходы на покупку продовольственных товаров в общих расходах, %, у
|
Среднедневная заработная плата одного работающего, руб., х
|
Удмуртская респ.
|
68,8
|
45,1
|
Свердловская обл.
|
61,2
|
59,0
|
Башкортостан
|
59,9
|
57,2
|
Челябинская обл.
|
56,7
|
61,8
|
Пермская обл.
|
55,0
|
58,8
|
Курганская обл.
|
54,3
|
47,2
|
Оренбургская обл.
|
49,3
|
55,2
|
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы.
2. Оценить каждую модель через среднюю ошибку аппроксимации  и F-критерий Фишера. и F-критерий Фишера.
Решение
1а. Для расчета параметров а и b линейной регрессии у = а + b х решаем систему нормальных уравнений относительно а и b:
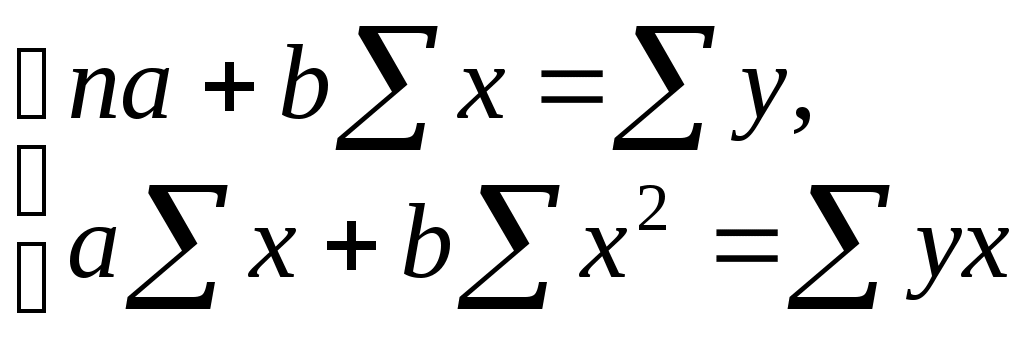 . .
По исходным данным рассчитываем 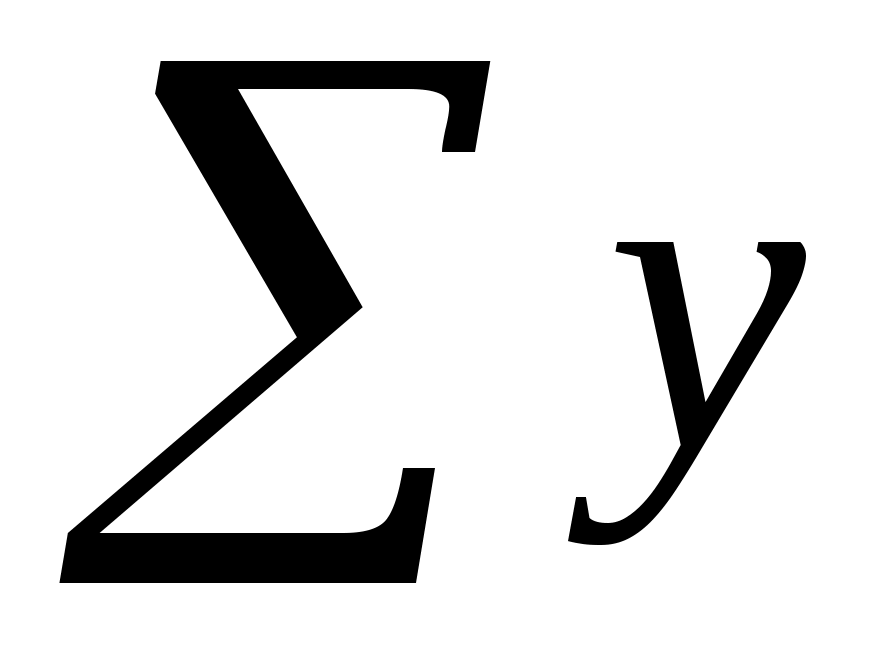 , , 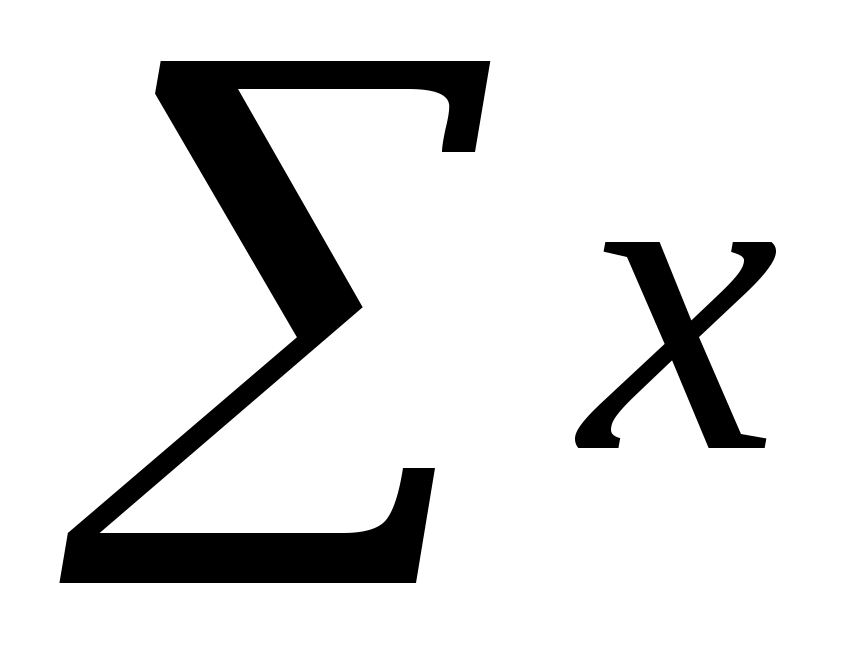 , , 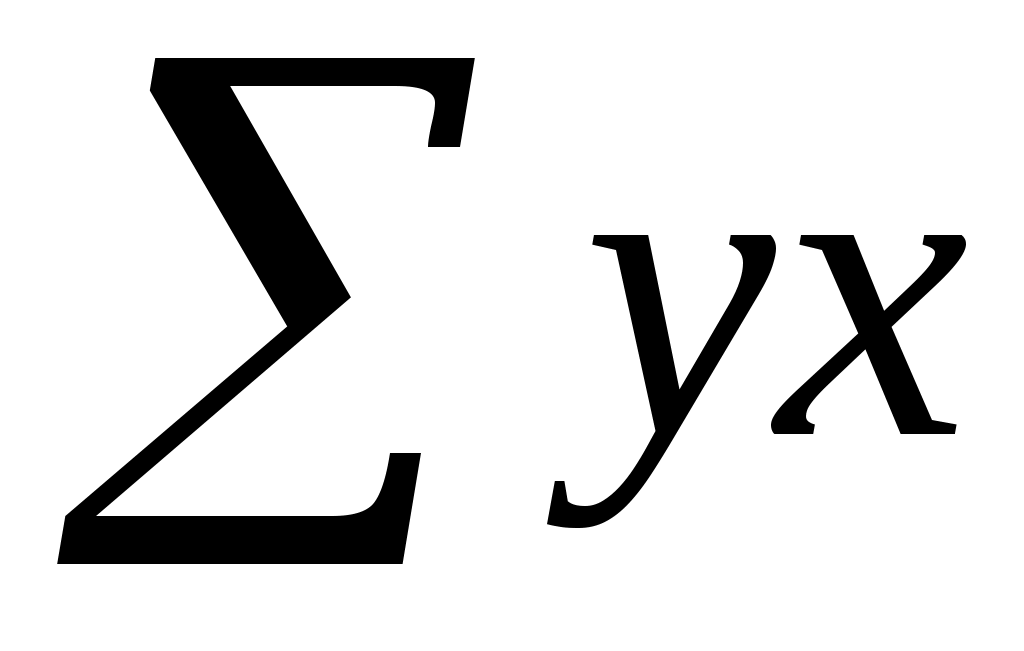 , , 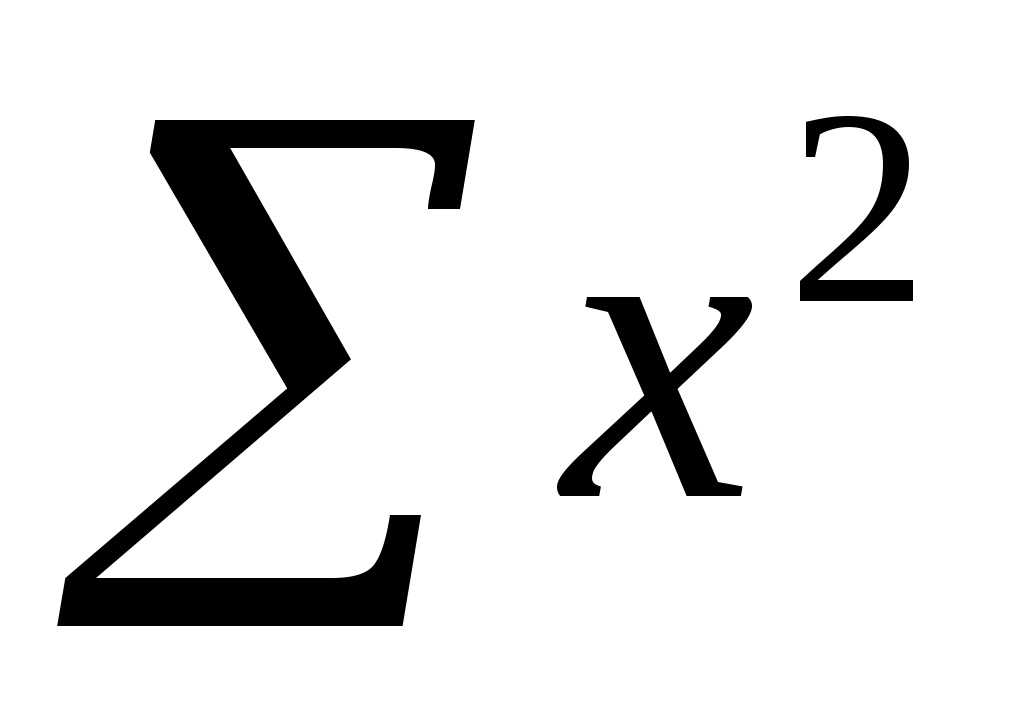 , , 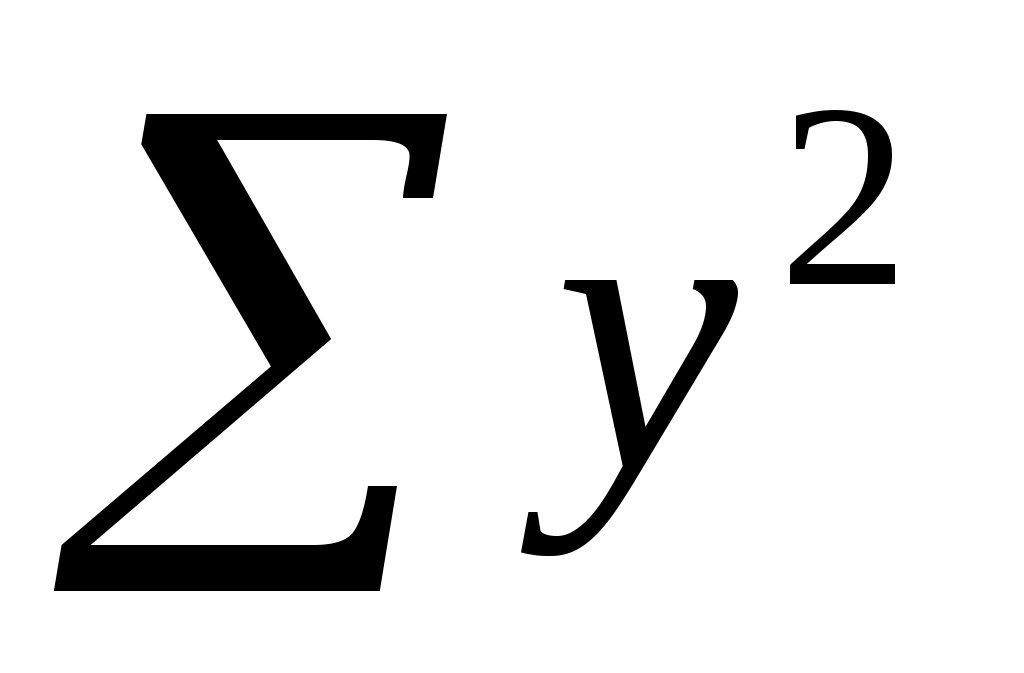 . .
Таблица 1.2
|
y
|
x
|
yx
|
x2
|
y2
|
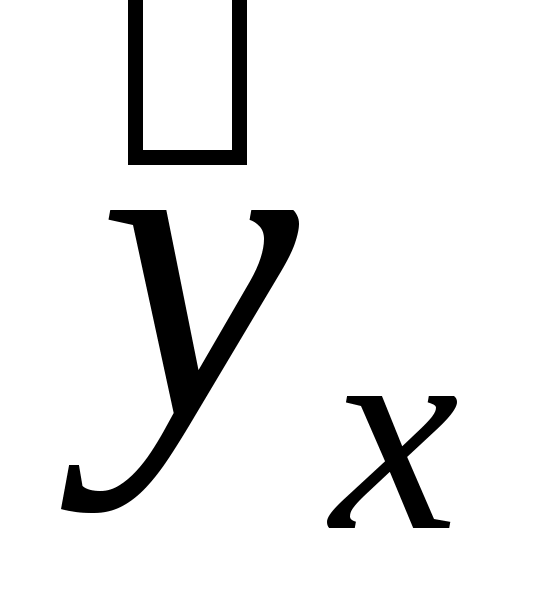
|
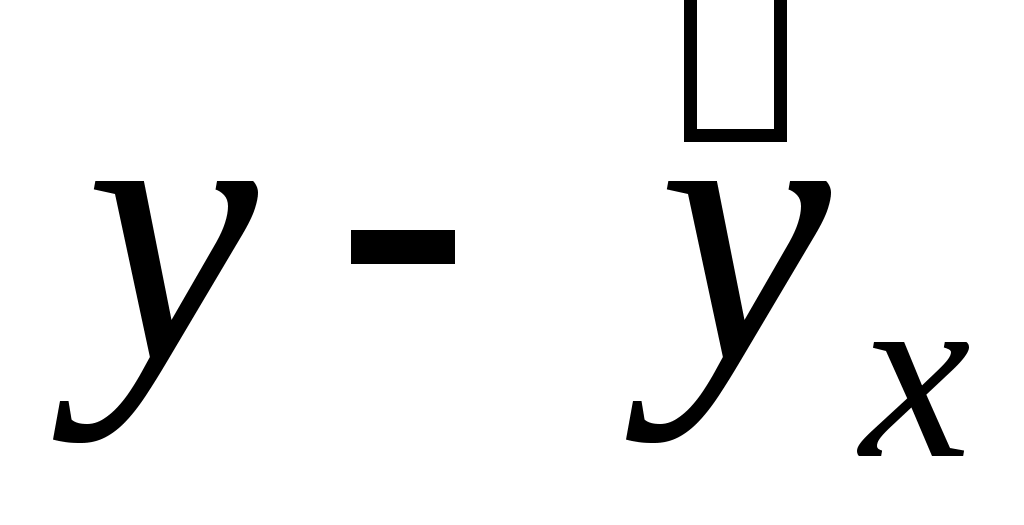
|

|
1
|
68.8
|
45.1
|
3102.88
|
2034.01
|
4733.44
|
61.3
|
7.5
|
10.9
|
2
|
61.2
|
59.0
|
3610.80
|
3481.00
|
3745.44
|
56.5
|
4.7
|
7.7
|
3
|
59.9
|
57.2
|
3426.28
|
3271.84
|
3588.01
|
57.1
|
2.8
|
4.7
|
4
|
56.7
|
61.8
|
3504.06
|
3819.24
|
3214.89
|
55.5
|
1.2
|
2.1
|
5
|
55.0
|
58.8
|
3234.00
|
3457.44
|
3025.00
|
56.5
|
-1.5
|
2.7
|
6
|
54.3
|
47.2
|
2562.96
|
2227.84
|
2948.49
|
60.5
|
-6.2
|
11.4
|
7
|
49.3
|
55.2
|
2721.36
|
3074.04
|
2430.49
|
57.8
|
-8.5
|
17.2
|
Итого
|
405.2
|
384.3
|
22162.34
|
21338.41
|
23685.76
|
405.2
|
0.0
|
56.7
|
Среднее значение
|
57.89
|
54.90
|
3166.05
|
3048.34
|
3383.68
|
*
|
*
|
8.1
|
|
5.74
|
5.86
|
*
|
*
|
*
|
*
|
*
|
*
|
2
|
32.92
|
34.34
|
*
|
*
|
*
|
*
|
*
|
*
|
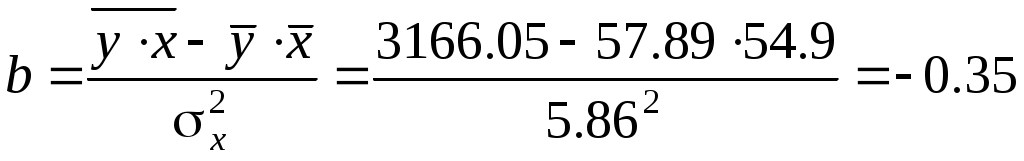 , ,
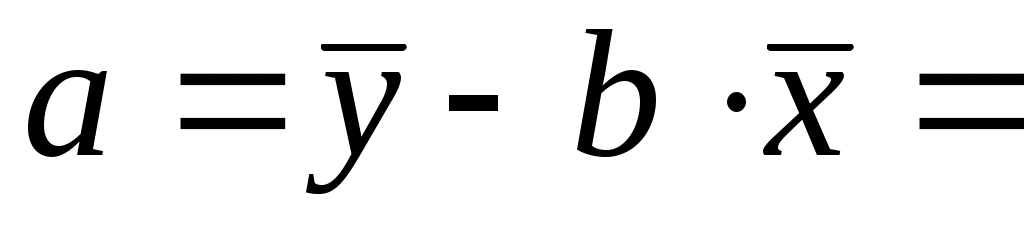 57,89+0,3554,9=76,88. 57,89+0,3554,9=76,88.
Уравнение регрессии:  = 76,88 - 0,35х. С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ных пункта. = 76,88 - 0,35х. С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ных пункта.
Рассчитаем линейный коэффициент парной корреляции:
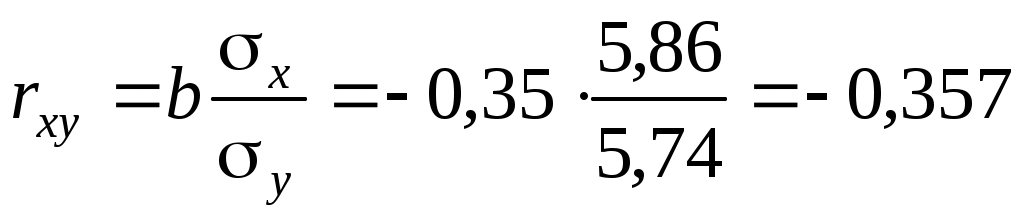 . .
Связь умеренная, обратная.
Определим коэффициент детерминации:
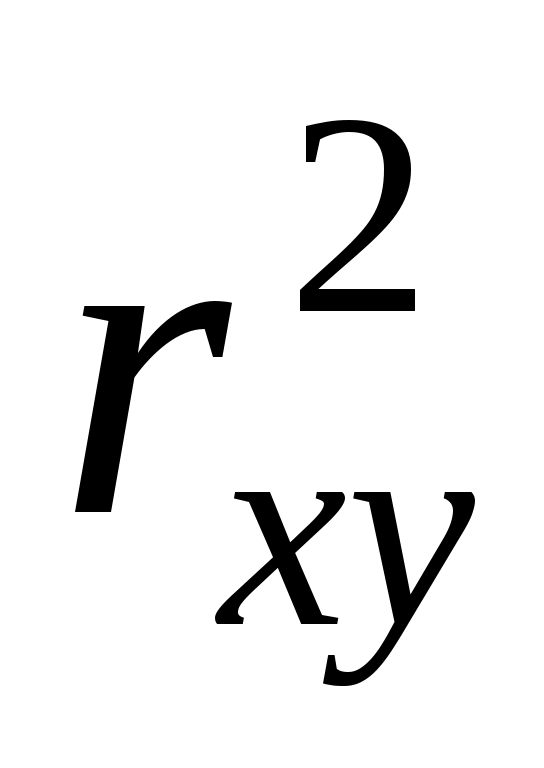 = (-0,35)2 = 0,127. = (-0,35)2 = 0,127.
Вариация результата на 12,7% объясняется вариацией факторах. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения 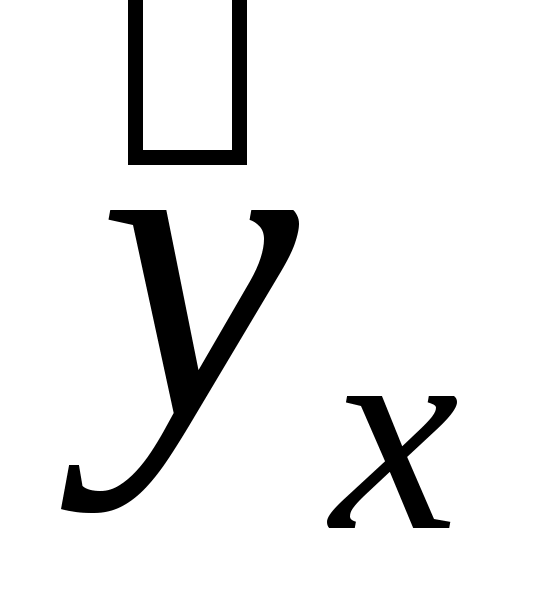 . Найдем величину средней ошибки аппроксимации . Найдем величину средней ошибки аппроксимации  : :
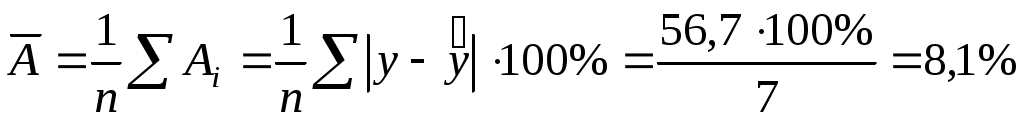 . .
В среднем расчетные значения отклоняются от фактических на 8,1%.
Рассчитаем F-критерий:
Fфакт = 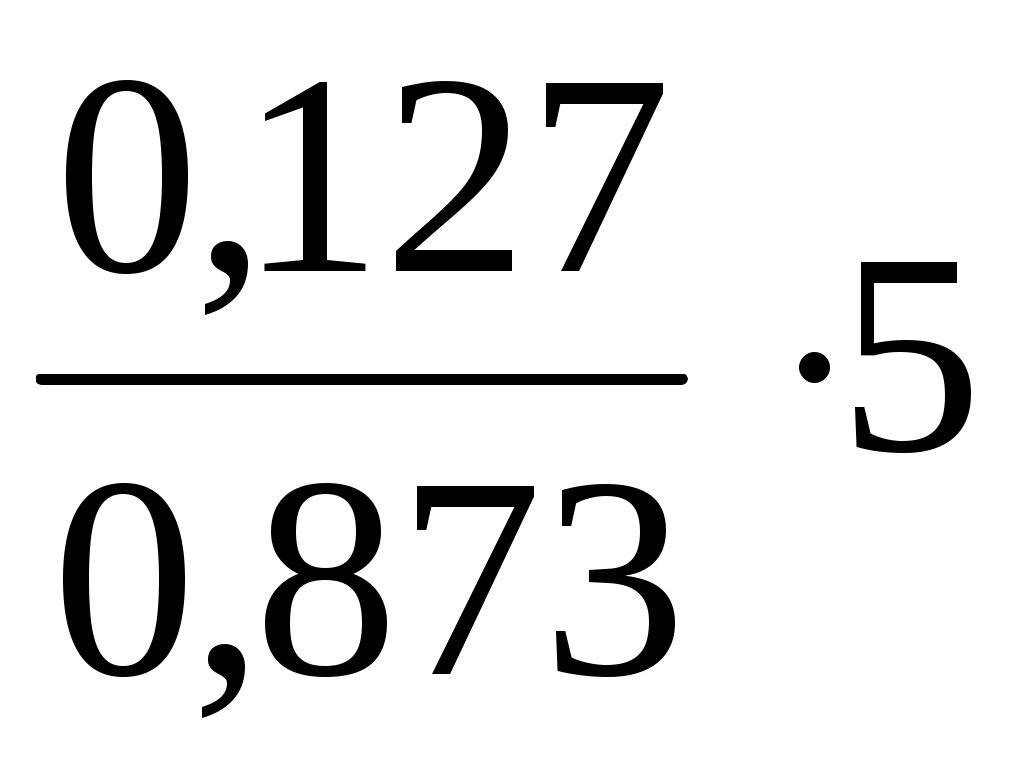 = 0,7. = 0,7.
Поскольку 1 F , следует рассмотреть F–1.
Полученное значение указывает на необходимость принять гипотезу Н0о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
1б. Построению степенной модели у = а хb предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
lgy = lga + blgx;
Y = C + bX,
Для расчетов используем данные табл. 1.3.
Таблица 1.3
|
Y
|
X
|
YX
|
Y2
|
X2
|
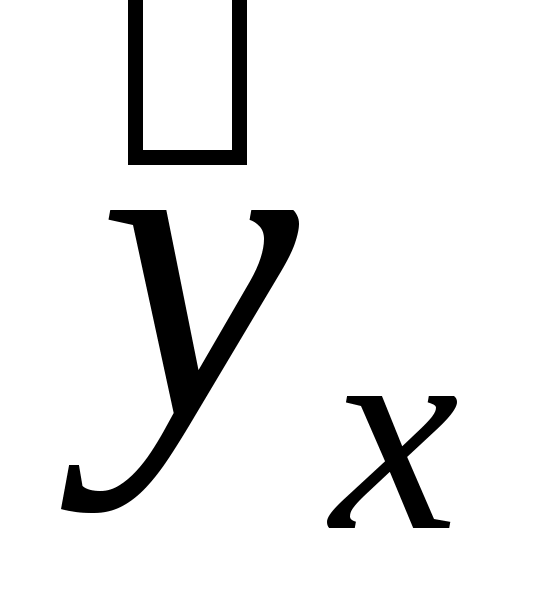
|
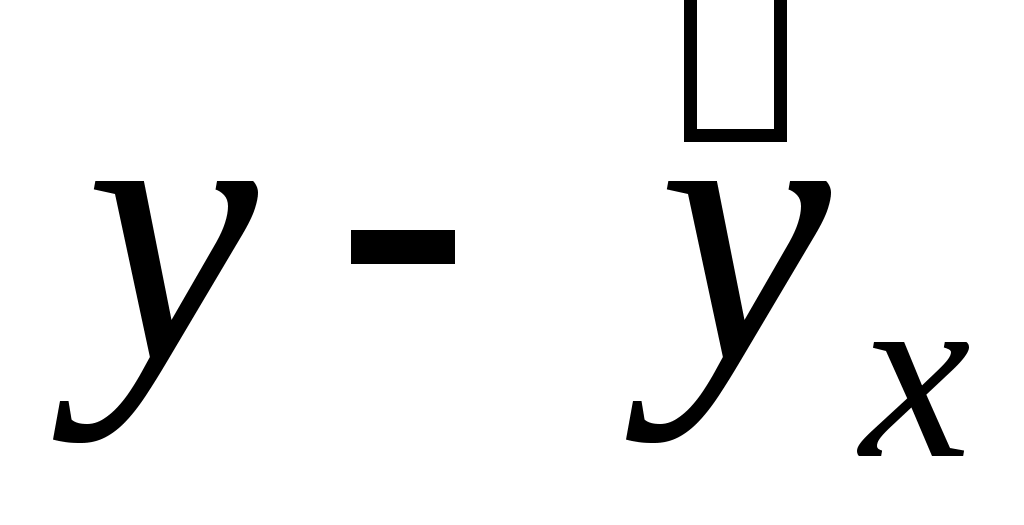
|
(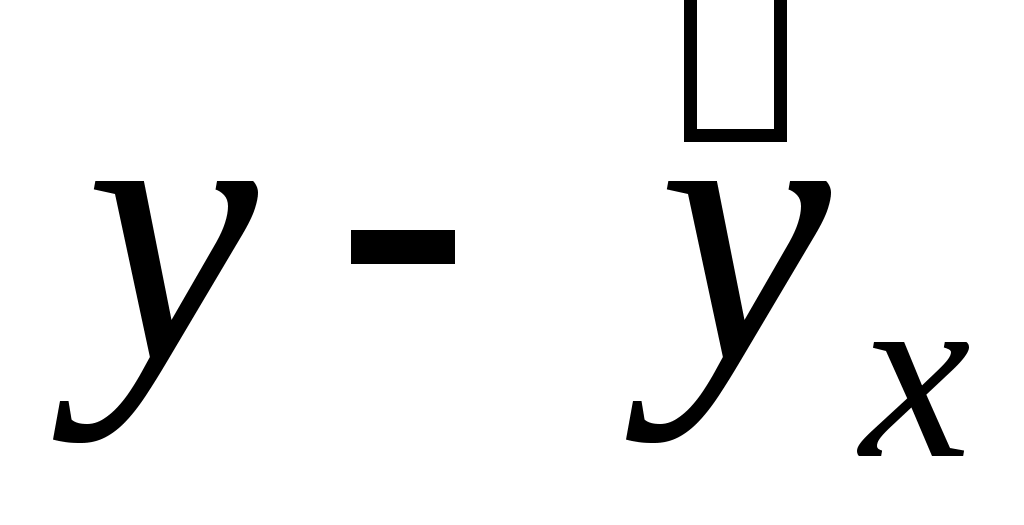 )2 )2
|
|
1
|
1.8376
|
1.6542
|
3.0398
|
3.3768
|
2.7364
|
61.0
|
7.8
|
60.8
|
11.3
|
2
|
1.7868
|
1.7709
|
3.1642
|
3.1927
|
3.1361
|
56.3
|
4.9
|
24.0
|
8.0
|
3
|
1.7774
|
1.7574
|
3.1236
|
3.1592
|
3.0885
|
56.8
|
3.1
|
9.6
|
5.2
|
4
|
1.7536
|
1.7910
|
3.1407
|
3.0751
|
3.2077
|
55.5
|
1.2
|
1.4
|
2.1
|
5
|
1.7404
|
1.7694
|
3.0795
|
3.0290
|
3.1308
|
56.3
|
-1.3
|
1.7
|
2.4
|
6
|
1.7348
|
1.6739
|
2.9039
|
3.0095
|
2.8019
|
60.2
|
-5.9
|
34.8
|
10.9
|
7
|
1.6928
|
1.7419
|
2.9487
|
2.8656
|
3.0342
|
57.4
|
-8.1
|
65.6
|
16.4
|
Итого
|
12.3234
|
12.1587
|
214003
|
21.7078
|
21.1355
|
403.5
|
1.7
|
197.9
|
56.3
|
Среднее значение
|
1.7605
|
1.7370
|
3.0572
|
3.1011
|
3.0194
|
*
|
*
|
28.27
|
8.0
|
|
0.0425
|
0.0484
|
*
|
*
|
*
|
*
|
*
|
*
|
*
|
2
|
0.0018
|
0.0023
|
*
|
*
|
*
|
*
|
*
|
*
|
*
|
Рассчитаем С и b:
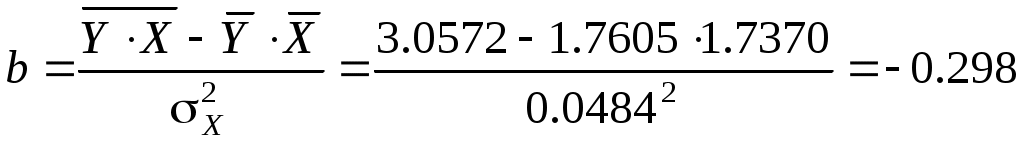 ; ;
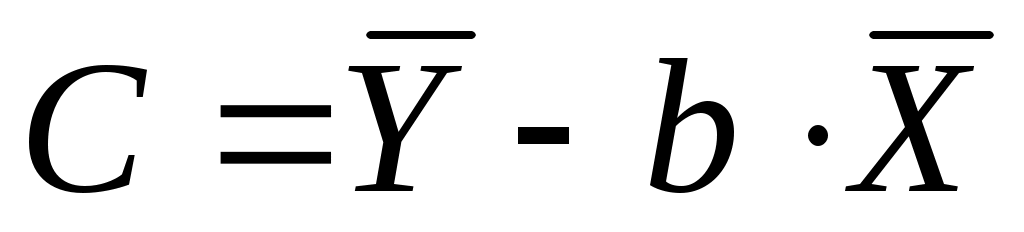 = 1.7605 - 1.298 * X. = 1.7605 - 1.298 * X.
Получим линейное уравнение:  = 2,278 - 0,298 * X. = 2,278 - 0,298 * X.
Выполнив его потенцирование, получим:
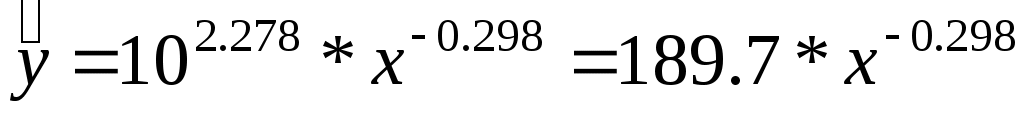 . .
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 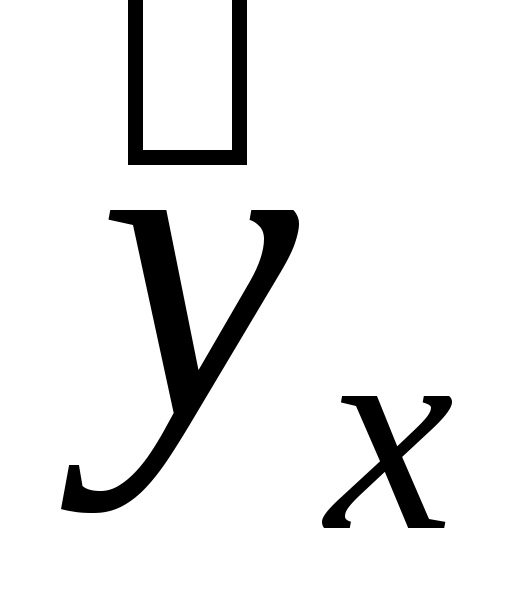 . По ним рассчитаем показатели: тесноты связи - индекс корреляции . По ним рассчитаем показатели: тесноты связи - индекс корреляции 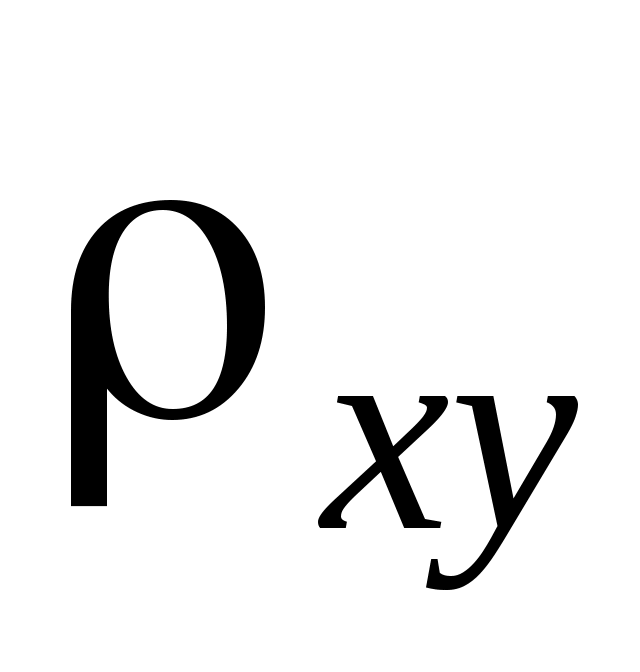 и среднюю ошибку аппроксимации и среднюю ошибку аппроксимации  : :
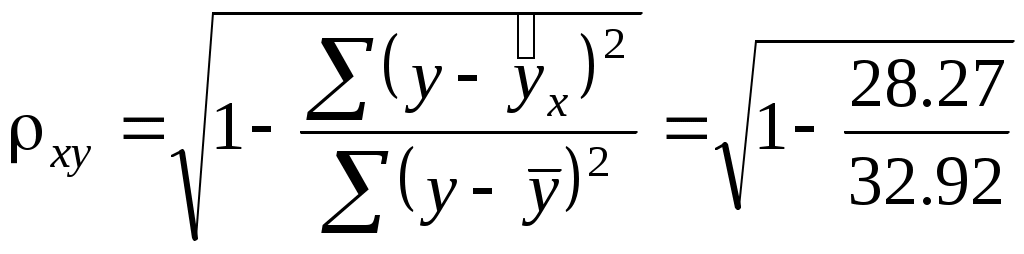 = 0.3758, = 0.3758, 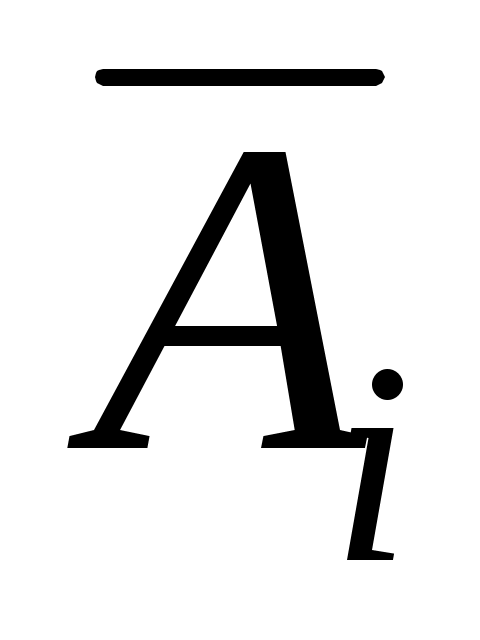 = 8.0%. = 8.0%.
Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь.
1в. Построению уравнения показательной кривой y=a*bx предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
lg y = lg a + x*lg b;
Y = C + B*x,
где Y = lg у, С = lg а, В = lg b.
Для расчетов используем данные табл. 1.4.
Таблица 1.4
|
Y
|
x
|
Yx
|
Y2
|
X2
|
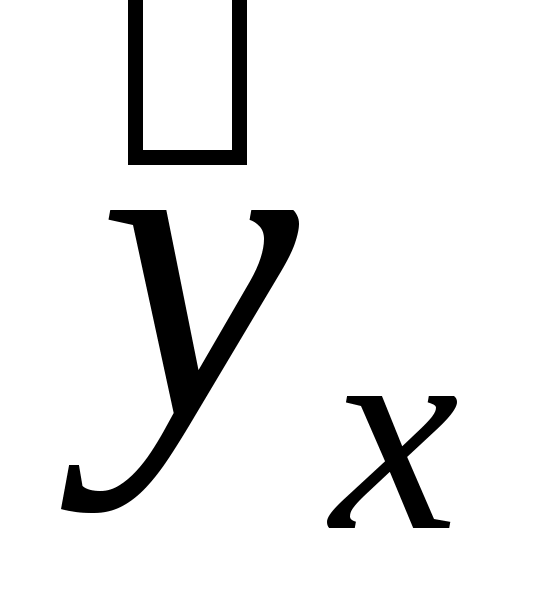
|
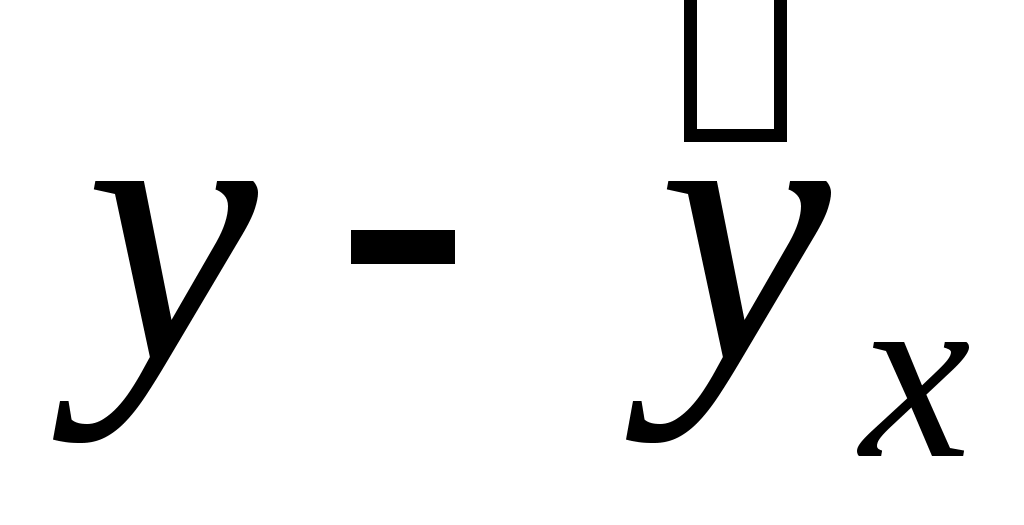
|
(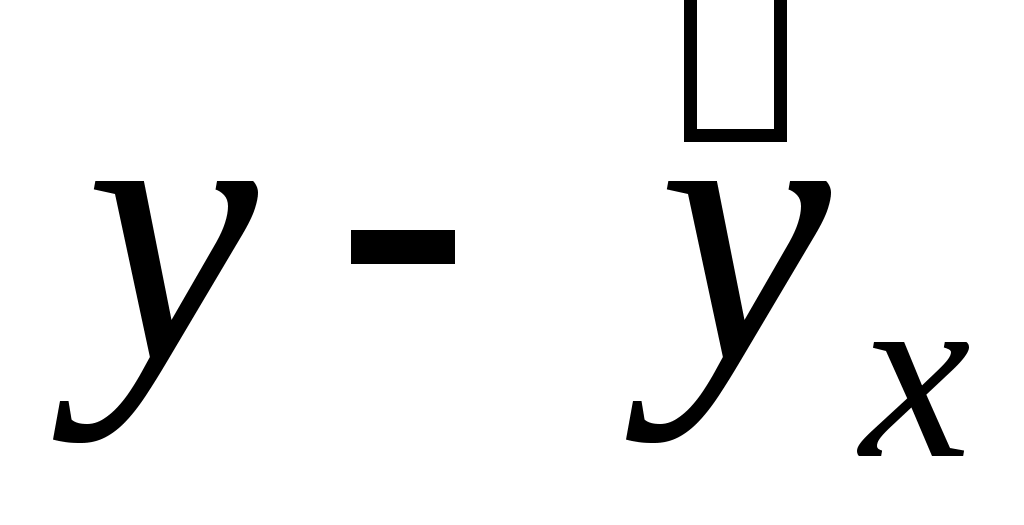 )2 )2
|

|
1
|
1.8376
|
45.1
|
82.8758
|
3.3768
|
2034.01
|
60.7
|
8.1
|
65.61
|
11.8
|
2
|
1.7868
|
59.0
|
105.4212
|
3.1927
|
3481.00
|
56.4
|
4.8
|
23.04
|
7.8
|
3
|
1.7774
|
57.2
|
108.3725
|
3.1592
|
3271.84
|
56.9
|
3.0
|
9.00
|
5.0
|
4
|
1.7536
|
61.8
|
102.3355
|
3.0751
|
3819.24
|
55.5
|
1.2
|
1.44
|
2.1
|
5
|
1.7404
|
58.8
|
81.8826
|
3.0290
|
3457.44
|
56.4
|
-1.4
|
1.96
|
2.5
|
6
|
1.7348
|
47.2
|
93.4426
|
3.0095
|
2227.84
|
60.0
|
-5.7
|
32.49
|
10.5
|
7
|
1.6928
|
55.2
|
675.9974
|
2.8656
|
3047.04
|
57.5
|
-8.2
|
67.24
|
16.6
|
Итого
|
12.3234
|
384.3
|
96.5711
|
21.7078
|
21338.41
|
403.4
|
-1.8
|
200.78
|
56.3
|
Среднее значение
|
1.7605
|
54.9
|
*
|
3.1011
|
*
|
*
|
*
|
28.68
|
8.0
|
|
0.0425
|
5.86
|
*
|
*
|
*
|
*
|
*
|
*
|
*
|
2
|
0.0018
|
34.3396
|
|
*
|
*
|
*
|
*
|
*
|
*
|
Значения параметров регрессии А и В составили:
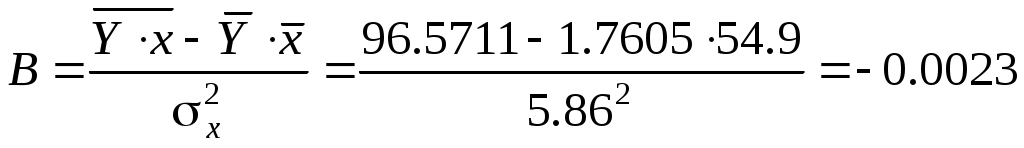 ; ;
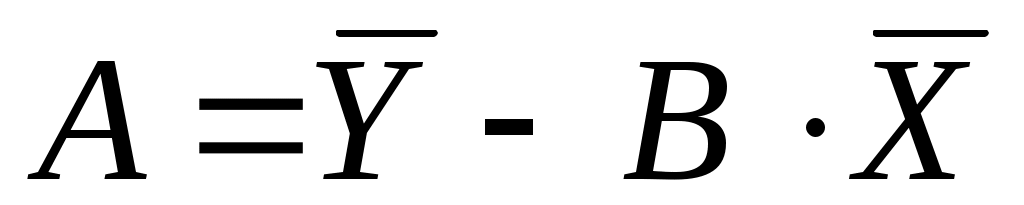 = 1.7605 - 0.0023 * 54.9 = 1.887. = 1.7605 - 0.0023 * 54.9 = 1.887.
Получено линейное уравнение:  = 1,887 - 0,0023 * х. = 1,887 - 0,0023 * х.
Произведем потенцирование полученного уравнения и запишем его в обычной форме:
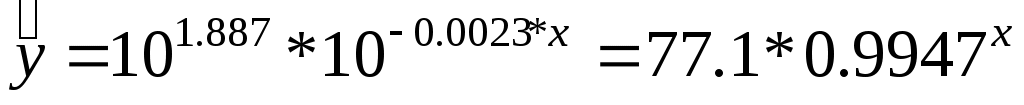 . .
Тесноту связи оценим через индекс корреляции 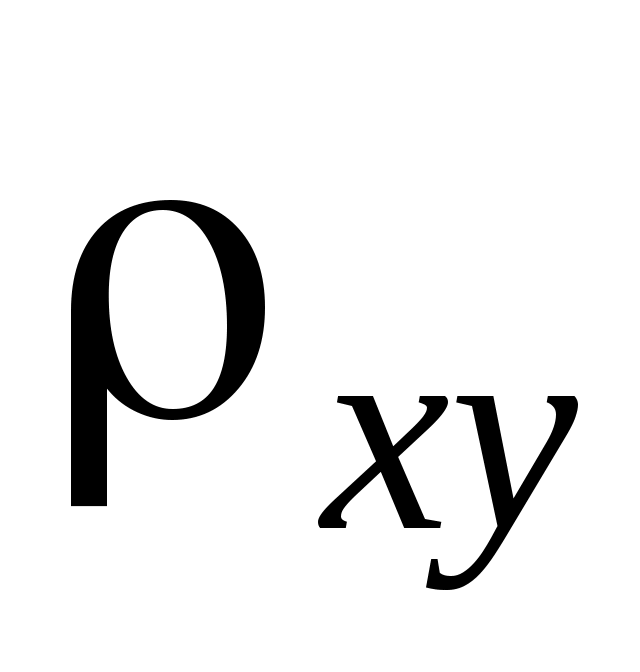 : :
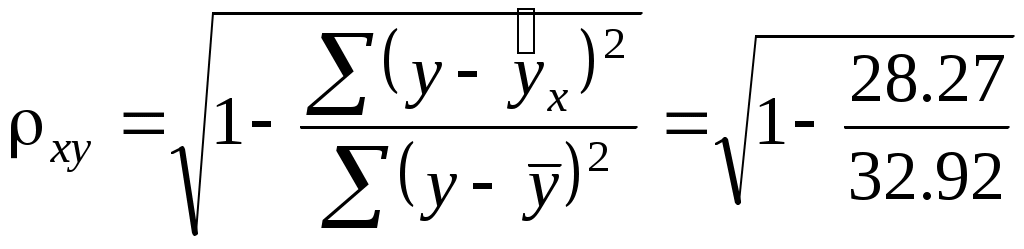 = 0.3589. = 0.3589.
Связь умеренная.
 = 8,0%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, она описывает изучаемую зависимость. = 8,0%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, она описывает изучаемую зависимость.
|
 Скачать 4.16 Mb.
Скачать 4.16 Mb.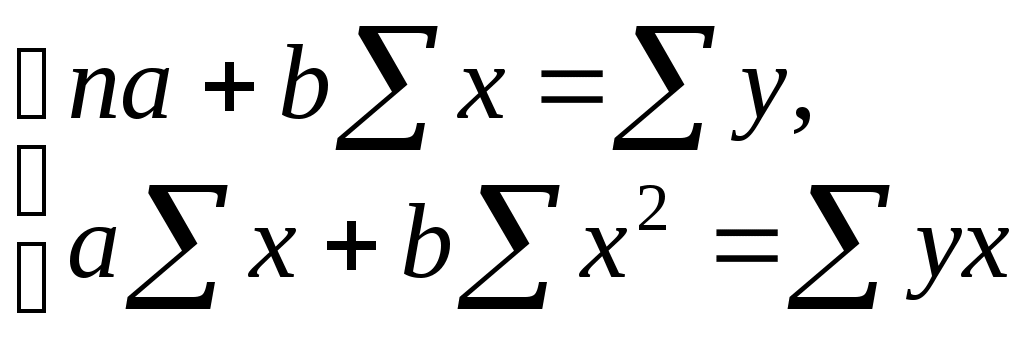 .
.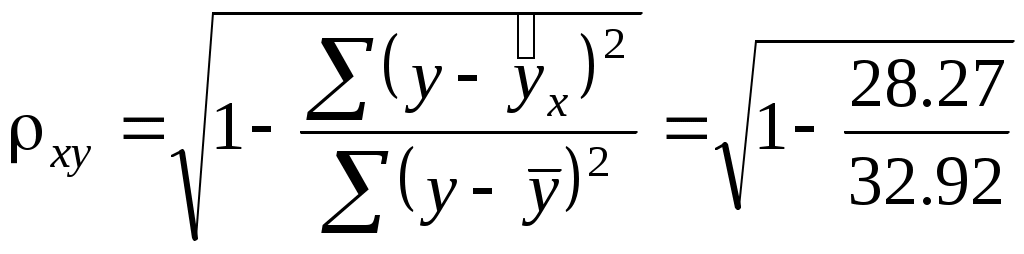 = 0.3758,
= 0.3758, 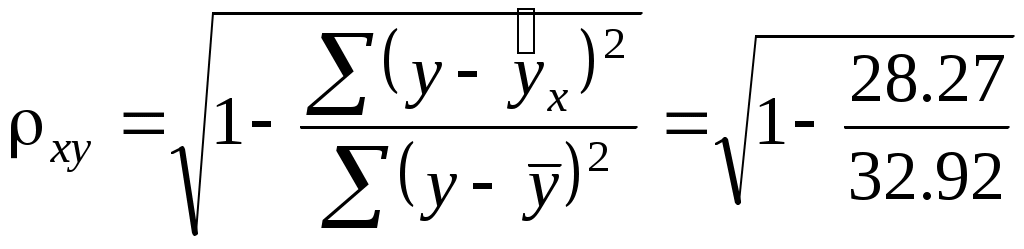 = 0.3589.
= 0.3589.