Эконометрика-Практикум-Елисеева. Практикум по эконометрике под редакцией членакорреспондента Российской Академии наук И. И. Елисеевой

• Название: Практикум по эконометрике под редакцией членакорреспондента Российской Академии наук И. И. Елисеевой
• Дата: 17.06.2022
• Размер: 4.16 Mb.
• Имя файла: Эконометрика-Практикум-Елисеева.doc
• Тип: Практикум; #599190
• страница: 9 из 26

2.3. РЕАЛИЗАЦИЯ ТИПОВЫХ ЗАДАЧ НА КОМПЬЮТЕРЕ

1. Решение примера проведем с использованием ППП MS Excel и Statgraphics.

Решение с помощью ППП Excel

Сводную таблицу основных статистических характеристик для одного или нескольких массивов данных можно получить с помощью инструмента анализа данных Описательная статистика. Для этого выполните следующие шаги:

1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2) в главном меню выберите последовательно пункты Сервис/Анализ данных/Описательная статистика, после чего щелкните по кнопке ОК;

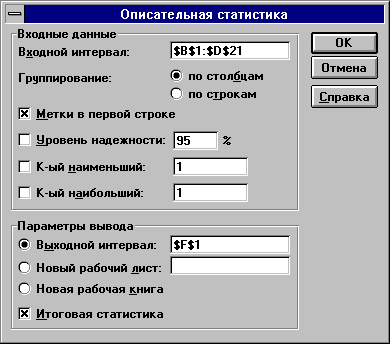
Рис. 2.1. Диалоговое окно ввода параметров инструмента Описательная статистика

3) заполните диалоговое окно ввода данных и параметров вывода (рис. 2.1):

Входной интервал - диапазон, содержащий анализируемые данные, это может быть одна или несколько строк (столбцов);

Группирование - по столбцам или по строкам - необходимо указать дополнительно;

Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист - можно задать произвольное имя нового листа.

Если необходимо получить дополнительную информацию Итоговой статистики. Уровня надежности, k-го наибольшего и наименьшего значений, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК.

Результаты вычисления соответствующих показателей для каждого признака представлены на рис. 2.2.

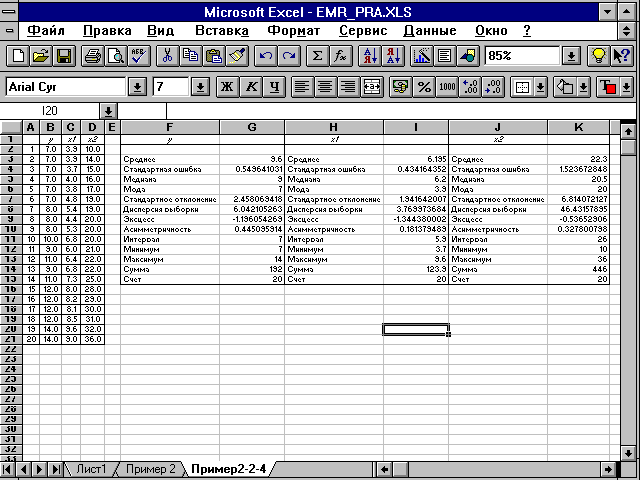
Рис. 2.2. Результат применения инструмента Описательная статистика

Решение с помощью ППП Statgraphics

Для проведения многофакторного анализа в ППП Statgraphics используется пункт меню Multiple Variable Analysis. Для получения показателей описательной статистики необходимо проделать следующие операции:

1) ввести исходные данные или открыть существующий файл, содержащий анализируемые данные;

2) в главном меню выбрать Describe/Numeric Data/Multiple Variable Analysis;

3) заполнить диалоговое окно ввода данных (рис. 2.3). Ввести названия всех столбцов, значения которых вы хотите включить в анализ;

щелкнуть по кнопке ОК;

XXXXX

Рис. 2.3. Диалоговое окно ввода данных

4) в окне табличных настроек поставить флажок напротив SummaryStatistics (рис. 2.4). Итоговая статистика - показатели вариации - появится в отдельном окне.

XXXXX

Рис. 2.4. Окно табличных настроек Multiple Variable Analysis

Для данных примера 4 результат применения функции Multiple Variable Analysis представлен на рис. 2.5.

XXXXX

Рис. 2.5. Итоговая статистика

Сравнивая значения средних квадратических отклонений и средних величин и определяя коэффициенты вариации:

;

;

,

приходим к выводу о повышенном уровне варьирования признаков, хотя и в допустимых пределах, не превышающих 35%. Совокупность предприятий однородна, и для ее изучения могут использоваться метод наименьших квадратов и вероятностные методы оценки статистических гипотез.

2. Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.

Решение с помощью ППП Excel

К сожалению, в ППП MS Excel нет специального инструмента для расчета линейных коэффициентов частной корреляции. Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого:

1) в главном меню последовательно выберите пункты Сервис/Анализ данных/Корреляция. Щелкните по кнопке ОК;

2) заполните диалоговое окно ввода данных и параметров вывода (см. рис. 2.1);

3) результаты вычислений - матрица коэффициентов парной корреляции - представлены на рис. 2.6.

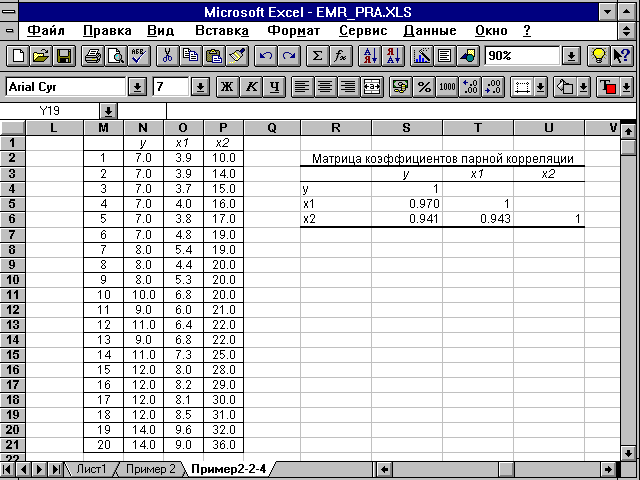
Рис. 2.6. Матрица коэффициентов парной корреляции

Решение с помощью ППП Statgraphics

При проведении многофакторного анализа - Multiple Variable Analysis - вычисляются линейные коэффициенты парной корреляции и линейные коэффициенты частной корреляции. Последовательность операций описана в п.1 этого примера. Для отображения результатов вычисления на экране необходимо установить флажки напротив Correlations и PartialCorrelations в окне табличных настроек (рис. 2.7).

XXXXX

Рис. 2.7. Окно табличных настроек Multiple Variable Analysis

В результате получим матрицы коэффициентов парной и частной корреляции (рис. 2.8).

XXXXX

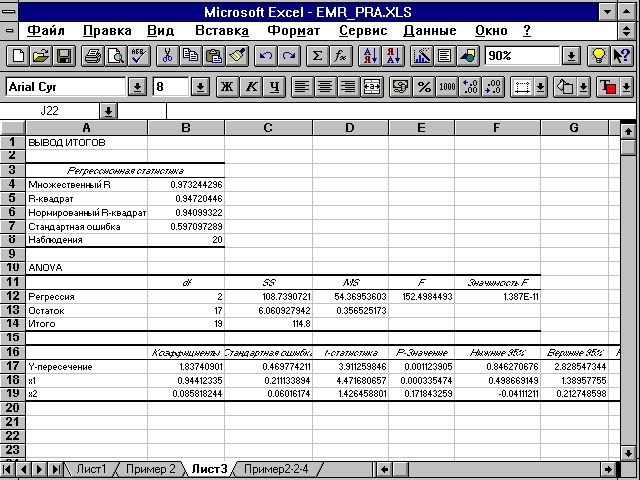
Рис. 2.8. Матрицы коэффициентов парной и частной корреляции 72

Значения коэффициентов парной корреляции указывают на весьма тесную связь выработки у как с коэффициентом обновления основных фондов -x₁, так и с долей рабочих высокой квалификации - x₂ ( = 0,9699 и = 0,9408). Но в то же время межфакторная связь = 0,9428 весьма тесная и превышает тесноту связи x₂ с у. В связи с этим для улучшения данной модели можно исключить из нее фактор x₂ как малоинформативный, недостаточно статистически надежный.

Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции, так как очищают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели. Наиболее тесно связаны y и x₁: - 0,7335, связь у и x₂ гораздо слабее: = 0,3247, а межфакторная зависимость x₁ и x₂ выше, чем парная у и x₂: = 0,3247 < = 0,3679. Все это приводит к выводу о необходимости исключить фактор x₂ - доля высококвалифицированных рабочих - из правой части уравнения множественной регрессии.

Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи:

= 0,9699; = 0,7335; = 0,9408; = 0,3247.

Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.

3. Вычисление параметров линейного уравнения множественной регрессии.

Решение с помощью ППП Excel

Эта операция проводится с помощью инструмента анализа данных Регрессия. Она аналогична расчету параметров парной линейной регрессии, описанной в 1-м разделе практикума, только в отличие от парной регрессии в диалоговом окне при заполнении параметра входной интервал Х следует указать не один столбец, а все столбцы, содержащие значения факторных признаков. Результаты анализа представлены на рис. 2.9.

Рис. 2.9. Результат применения инструмента Регрессия

Решение с помощью ППП Statgraphics

Для вычисления параметров множественной регрессии можно использовать процедуру Multiple Regression. Для этого:

1) введите исходные данные или откройте существующий файл;

2) в главном меню последовательно выберите Relate / Multiple Regression;

3) заполните диалоговое окно ввода данных. В поле DependedVariable введите название столбца, содержащего значения зависимой переменной, в поле IndependedVariable - названия столбцов, содержащих значения факторов. Щелкните по кнопке ОК.

Результаты вычисления функции Multiple Regression появятся в отдельном окне (рис. 2.10).

По результатам вычислений составим уравнение множественной регрессии вида

;

.

Значения случайных ошибок параметров b₀,b₁ и b₂ с учетом округления:

= 0,4711; = 0,2126; =0,0605.

XXXXX

Рис. 2.10. Итоговое окно функции Multiple Regression

Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Эти значения используются для расчета t-критерия Стьюдента:

= 3,90; = 4,45; = 1,42.

Если значения t-критерия больше 2-3, можно сделать вывод о существенности данного параметра, который формируется под воздействием неслучайных причин. Здесь статистически значимыми являются b₀ и b₁, а величина b₂ сформировалась под воздействием случайных причин, поэтому фактор x₂, силу влияния которого оценивает b₂, можно исключить как несущественно влияющий, неинформативный.

На это же указывает показатель вероятности случайных значений параметров регрессии: если  меньше принятого нами уровня (обычно 0,1; 0,05 или 0,01; это соответствует 10%; 5% или 1% вероятности), делают вывод о неслучайной природе данного значения параметра, т.е. о том, что он статистически значим и надежен. В противном случае принимается гипотеза о случайной природе значения коэффициентов уравнения. Здесь =17,5% > 5%, что позволяет рассматривать x₂ как неинформативный фактор и удалить его для улучшения данного уравнения.

Величина b₀ оценивает агрегированное влияние прочих (кроме учтенных в модели факторов x₁ и x₂) факторов на результат y.

Величины b₁ и b₂ указывают, что с увеличением x₁ и x₂ на единицу их значений результат увеличивается соответственно на 0,9459 и на 0,0856 млн руб. Сравнивать эти значения не следует, так как они зависят от единиц измерения каждого признака и потому несопоставимы между собой.

4. Оценку надежности уравнения регрессии в целом и показателя тесноты связи , дает F-критерий Фишера:

F_факт = .

По данным таблиц дисперсионного анализа, представленным на рис. 2.9 и 2.10, F_факт⁼ 151,65 . Вероятность случайно получить такое значение F-критерия составляет 0,0000, что не превышает допустимый уровень значимости 5%; об этом свидетельствует величина Р - значения из этих же таблиц. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи .

Значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации приведены на рис. 2.9 и 2.10 в рамках регрессионной статистики.

Нескорректированный коэффициент множественной детерминации = 0,9469 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 94,7% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами - на весьма тесную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации = 0,9407 определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 90%) детерминированность результата у в модели факторами x₁ и x₂.

5. Информация для оценки с помощью частных F-критериев Фишера целесообразности включения в модель фактора x₁ после фактора x₂ и фактора x₂ после фактора x₁ может быть получена в ППП Statgraphics следующим образом:

1) введите исходные данные или откройте существующий файл;

2) в главном меню последовательно выберите пункты Relate / Multiple Regression;

3) заполните диалоговое окно ввода данных. В поле DependedVariable введите название столбца, содержащего значения зависимой переменной, в поле IndependedVariable - названия столбцов, содержащих значения факторов, в том порядке, в котором будет проводиться анализ целесообразности включения факторов в модель. Чтобы оценить статистическую значимость включения в модель фактора x₁после фактора x₂, сначала введите фактор x₁, затем x₂. Для оценки обратного порядка включения факторов в модель x₂ после x₁ введите x₂, затем x₁. Щелкните по кнопке ОК;

4) в окне табличных настроек поставьте флажок напротив поля ConditionalSumsofSquares.

Результаты вычисления показаны на рис. 2.11.

Рис. 2.11. Результаты вычисления частных F-критериев Фишера

Частный F-критерий - F_частн показывает статистическую значимость включения фактора x₂ в модель после того, как в нее включен фактор x₁.

F_частн ⁼ 2. Вероятность случайной природы его значения (Р-значение = 0,1750) составляет 17,5% против принятого уровня значимости  = 0,05, (5%). Следовательно, включение в модель фактора х₂ - доля высококвалифицированных рабочих - после того, как в уравнение включен фактор х₁ - коэффициент обновления основных фондов - статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака х₂ оказывается незначимым, несущественным; фактор х₂ включать в уравнение после фактора х₁ не следует.

Если поменять первоначальный порядок включения факторов в модель и рассмотреть вариант включения х₁ после х₂, то результат расчета частного F-критерия для х₁ будет иным. F_частн = 19,80. Вероятность его случайного формирования составила 0,04%, это значительно меньше принятого стандарта  = 0,05 (5%). Следовательно, значение частного F-критерия для дополнительно включенного фактора х₁ не случайно, является статистически значимым, надежным, достоверным: прирост факторной дисперсии за счет дополнительного фактора х₁ является существенным. Фактор х₁ должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора х₂.

Общий вывод состоит в том, что множественная модель с факторами х₁ и х₂с = 0,9469 содержит неинформативный фактор х₂. Если исключить фактор х₂, то можно ограничиться уравнением парной регрессии:

, = 0,9407,

более простым, хорошо детерминированным, пригодным для анализа и для прогноза.

6. Средние частные коэффициенты эластичности показывают, на сколько процентов от значения своей средней изменяется результат при изменении фактора х_j на 1% от своей средней и при фиксированном воздействии на у всех прочих факторов, включенных в уравнение регрессии. Для линейной зависимости

,

где b_j - коэффициент регрессии при x_j в уравнении множественной регрессии. Здесь

= 0,6099%,

= 0,1989%.

По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат у признака фактора х₁, чем признака фактора х₂: 0,6% против 0,2%.