Эконометрика-Практикум-Елисеева. Практикум по эконометрике под редакцией членакорреспондента Российской Академии наук И. И. Елисеевой
 Скачать 4.16 Mb.
|
2.2. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧПример 1 По 30 территориям России имеются данные, представленные в табл. 2.1. Таблица 2.1
Требуется: 1. Построить уравнение множественной регрессии в стандартизованной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с 1 и 2, пояснить различия между ними. 2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними. 3. Рассчитать общий и частные F-критерии Фишера. Решение 1. Линейное уравнение множественной регрессии у от х1 и х2 имеет вид: у = а + b1* х1 + b2* х2. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: ty = 1*  + 2* .Расчет -коэффициентов выполним по формулам 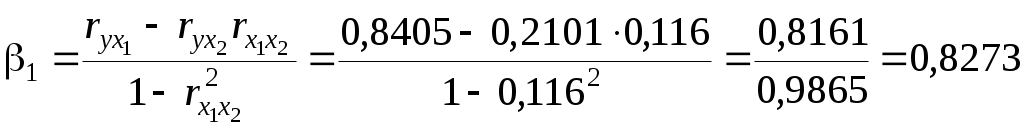 ; 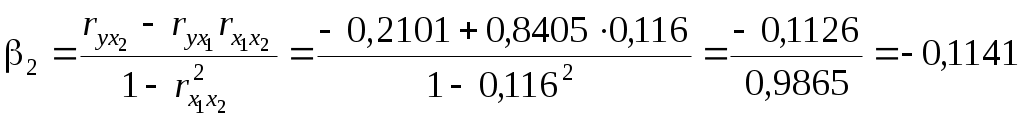.Получим уравнение  .Для построения уравнения в естественной форме рассчитаем b1 и b2, используя формулы для перехода от i к b i:  ;  ; ;  .Значение а определим из соотношения а =  = 86,8 – 1,61554,9 +2,2533,5 =-73,52, = -73,52 +1,62*x1 - 2,25*x2.Для характеристики относительной силы влияния x1 и x2 на у рассчитаем средние коэффициенты эластичности:  ; ;  .С увеличением средней заработной платы x1 на 1% от ее среднего уровня средний душевой доход у возрастает на 1,03% от своего среднего уровня; при повышении среднего возраста безработного x2на 1% среднедушевой дохода снижается на 0,87% от своего среднего уровня. Очевидно, что сила влияния средней заработной платы x1 на средний душевой доход у оказалась большей, чем сила влияния среднего возраста безработного x2. К аналогичным выводам о силе связи приходим при сравнении модулей значений 1 и 2:  .Различия в силе влияния фактора на результат, полученные при сравнении  и j, объясняются тем, что коэффициент эластичности исходит из соотношения средних: , а -коэффициент - из соотношения средних квадратических отклонений: .2. Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле: 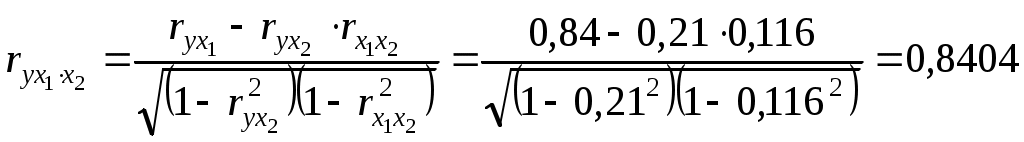 ; ;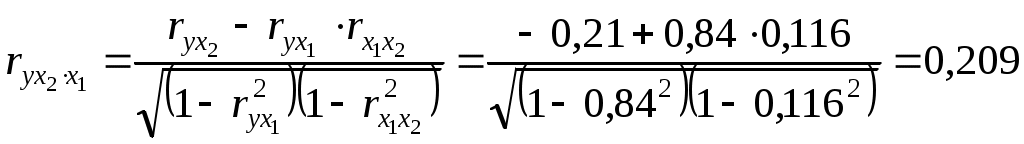 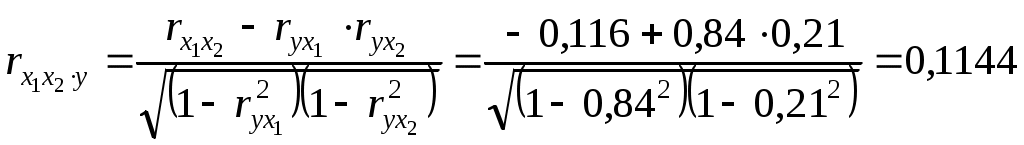.Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи (  =0,116) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают: = 0,8405;  = -0,2101;  = 0,1160; = 0,8404;  = -0,2092;  = 0,1144.Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов  и j: .Зависимость у от х1 и х2 характеризуется как тесная, в которой 72% вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28% от общей вариации у. 3. Общий F-критерий проверяет гипотезу Н0о статистической значимости уравнения регрессии и показателя тесноты связи (R2 = 0): Ffakt = 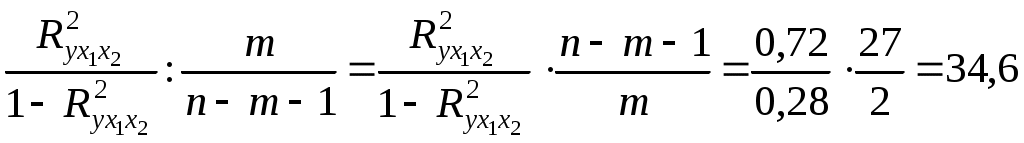 ;Ftabl = 3,4; = 0,05. Сравнивая Ftabl и Ffakt, приходим к выводу о необходимости отклонить гипотезу Н0, так как Ftabl = 3,4 < Ffakt = 34,6. С вероятностью 1 - = 0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи  , которые сформировались под неслучайным воздействием факторов x1 и x2. Частные F- критерии - Fx1 и Fx2 оценивают статистическую значимость присутствия факторов x1 и x2 в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. Fx1 оценивает целесообразность включения в уравнение фактора x1 после того, как в него был включен фактор x2. Соответственно Fx2 указывает на целесообразность включения в модель фактора x2 после фактора x1: 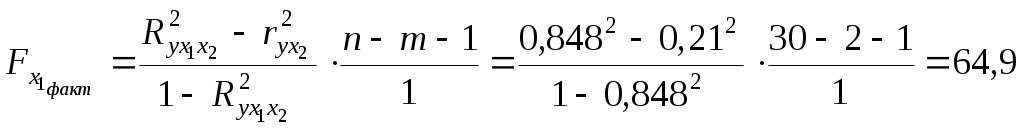 . = 4,21; =0,05.Сравнивая Fтабл и Fфакт, приходим к выводу о целесообразности включения в модель фактора х1 после фактора х2, так как  = 64,9 > Fтабл. Гипотезу Н0о несущественности прироста  за счет включения дополнительного фактора х1 отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора х1 после фактора х2.Целесообразность включения в модель фактора х2 после фактора х1 проверяет 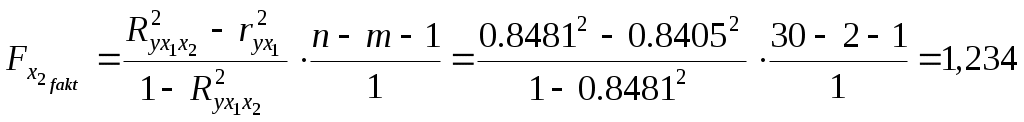 : .Низкое значение  (немногим больше 1) свидетельствует о статистической незначимости прироста  за счет включения в модель фактора x2 после фактора x1. Следовательно, подтверждается нулевая гипотеза Н0о нецелесообразности включения в модель фактора x2 (средний возраст безработного). Это означает, что парная регрессионная модель зависимости среднего дохода от средней заработной платы является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор x2 (средний возраст безработного).Пример 2 По 20 территориям России изучаются следующие данные (табл. 2.2): зависимость среднегодового душевого дохода у (тыс. руб.) от доли занятых тяжелым физическим трудом в общей численности занятых x1 (%) и от доли экономически активного населения в численности всего населения x2 (%). Таблица 2.2
Требуется: 1. Составить таблицу дисперсионного анализа для проверки при уровне значимости = 0,05 статистической значимости уравнения множественной регрессии и его показателя тесноты связи. 2. С помощью частных F-критериев Фишера оценить, насколько целесообразно включение в уравнение множественной регрессии фактора x1 после фактора x2 и насколько целесообразно включение x2после x1. 3. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов при переменных x1 и x2 множественного уравнения регрессии. Решение 1. Задача дисперсионного анализа состоит в проверке нулевой гипотезы Н0о статистической незначимости уравнения регрессии в целом и показателя тесноты связи. Анализ выполняется при сравнении фактического и табличного (критического) значений F-критерия Фишера Fтабл и Fфакт. Fфакт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: Fфакт = 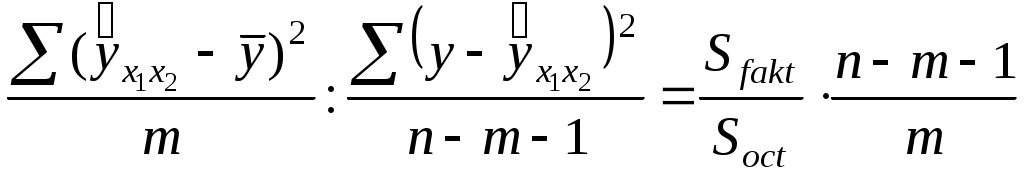 ,где п - число единиц совокупности; m - число факторов в уравнении линейной регрессии;  - фактическое значение результативного признака; - расчетное значение результативного признака.Результаты дисперсионного анализа представлены в табл. 2.3. Таблица 2.3
 = 19945.9; = 11918.3; = 8027.6; = 12.62.Сравнивая Fтабл и Fфакт, приходим к выводу о необходимости отклонить гипотезу Н0 и сделать вывод о статистической значимости уравнения регрессии в целом и значения  , так как они статистически надежны и сформировались под систематическим действием неслучайных причин. Вероятность того, что допускаются ошибки при отклонении нулевой гипотезы, не превышает 5%, и это является достаточно малой величиной.2. Частный F-критерий Фишера оценивает статистическую целесообразность включения фактора х1 в модель после того, как в нее включен фактор х2. Частный F-критерий Фишера строится как отношение прироста факторной дисперсии за счет дополнительно включенного фактора (на одну степень свободы) к остаточной дисперсии (на одну степень свободы), подсчитанной по модели с включенными факторами х1 и х2: 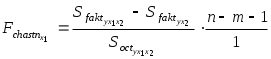 .Результаты дисперсионного анализа представлены в табл. 2.4. Таблица 2.4
= 19945.9; = 11918.3; = 5127.1; = 11918.3 - 5127.1 = 6791.2; = 8027.6;Включение фактора х1 после фактора х2 оказалось статистически значимым и оправданным: прирост факторной дисперсии (в расчете на одну степень свободы) оказался существенным, т.е. следствием дополнительного включения в модель систематически действующего фактора х1, так как  = 14,38 > Fтабл = 4,45 .Аналогично проверим целесообразность включения в модель дополнительного фактора х2 после включенного ранее фактора х1. Расчет выполним с использованием показателей тесноты связи 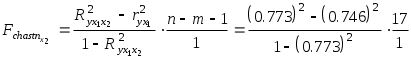и  : = 1.73.В силу того что  = 1.73 < Fтабл = 4.45, приходим к выводу, что включение х2 после х1 оказалось бесполезным: прирост факторной дисперсии в расчете на одну степень свободы был несуществен, статистически незначим, т.е. влияние х2 не является устойчивым, систематическим. Вполне возможно было ограничиться построением линейного уравнения парной регрессии y от х1.3. Оценка с помощью t-критерия Стьюдента значимости коэффициентов b1 и b2 связана с сопоставлением их значений с величиной их случайных ошибок: т  и т . Расчет значений случайных ошибок достаточно сложен и трудоёмок. Поэтому предлагается более простой способ: расчет значения t-критерия Стьюдента для коэффициентов регрессии линейного уравнения как квадратного корня из соответствующего частного F-критерия Фишера: = 3,79; = 1,32.Табличные (критические) значения t-критерия Стьюдента зависят от принятого уровня значимости (обычно это 0,1; 0,05 или 0,01) и от числа степеней свободы (п - т - 1), где п - число единиц совокупности, т - число факторов в уравнении. В нашем примере при = 0,05; df = 20 - 3 = 17; tтабл = 2,10. Сравнивая tтабл и tфакт, приходим к выводу, что, так как  = 3,79 > 2,11 = tтабл, коэффициент регрессии b1 является статистически значимым, надежным, на него можно опираться в анализе и в прогнозе. Так как  = 1,32 < 2,10 = tтабл, приходим к заключению, что величина b2 является статистически незначимой, ненадежной в силу того, что она формируется преимущественно под воздействием случайных факторов. Еще раз подтверждается статистическая значимость влияния х1(доли занятых тяжелым физическим трудом) на у (среднедушевой доход) и ненадежность, незначимость влияния х2 (доли экономически активного населения в численности всего населения).Пример 3 Зависимость спроса на свинину х1 от цены на нее х2 и от цены на говядину х3 представлена уравнением Ig х1 = 0,1274 - 0,2143*lg х2 + 2,8254*lg х3. Требуется: 1. Представить данное уравнение в естественной форме (не в логарифмах). 2. Оценить значимость параметров данного уравнения, если известно, что t-критерий для параметра b2 при х2 составил 0,827, а для параметра b3 при х3 - 1,015. Решение 1. Представленное степенное уравнение множественной регрессии приводим к естественной форме путём потенцирования обеих частей уравнения: х1 = 100.1274*х2-0.2143*х32.8254; х1 = 1.3409*  *х32.8254.Значения коэффициентов регрессии b1 и b2 в степенной функции равны коэффициентам эластичности результата х1 от х2 и х3.  = -0,2143%;  = 2,8254%.Спрос на свинину х1 сильнее связан с ценой на говядину - он увеличивается в среднем на 2,83% при росте цен на 1%. С ценой на свинину спрос на нее связан обратной зависимостью: с ростом цен на 1% потребление снижается в среднем на 0,21%. 2. Табличное значение t-критерия для = 0,05 обычно лежит в интервале 2 - 3 - в зависимости от степеней свободы. В данном примере  = 0,827,  = 1,015. Это весьма небольшие значения t-критерия, которые свидетельствуют о случайной природе взаимосвязи, о статистической ненадежности всего уравнения, поэтому применять полученное уравнение для прогноза не рекомендуется.Пример 4 По 20 предприятиям региона (табл. 2.5) изучается зависимость выработки продукции на одного работника у (тыс. руб.) от ввода в действие новых основных фондов х1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х2 (%). Таблица 2.5
Требуется: 1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения. 2. Проанализировать линейные коэффициенты парной и частной корреляции. 3. Написать уравнение множественной регрессии, оценить значимость его параметров, пояснить их экономический смысл. 4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и  . Сравнить значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации.5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора х1после х2 и фактора х2 после х1. 6. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат. |
= 0,8405
= -130,49+6,14* x1+4,13* x2
=74,4+7,1* x1
= -355,3+9,2*x2