Эконометрика-Практикум-Елисеева. Практикум по эконометрике под редакцией членакорреспондента Российской Академии наук И. И. Елисеевой
 Скачать 4.16 Mb.
|
|
1г. Уравнение равносторонней гиперболы у= а + b  линеаризуется при замене: z = . Тогда у = а + b*г. Для расчетов используем данные табл. 1.5.Таблица 1.5
Значения параметров регрессии а и b составили: а =  = 57,89 - 1051,4 * 0,0184 = 38,5; = 1051.4.Получено уравнение:  = 38,5 + 1051,4 * .Индекс корреляции:  = 0,3944. = 8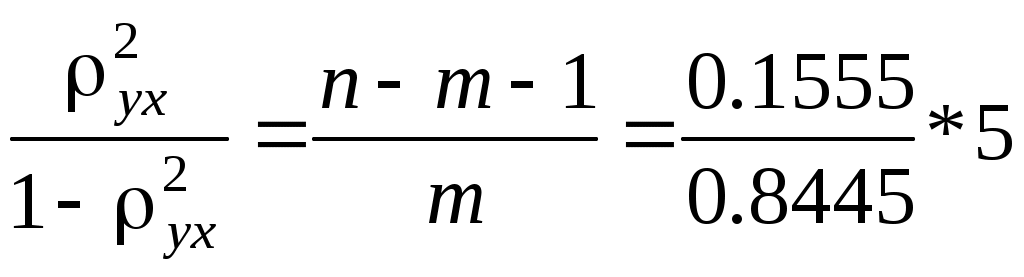,1%. По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи:  = 0,3944 (по сравнению с линейной, степенной и показательной регрессиями).  остается на допустимом уровне:2. Fфакт =  = 0,92,где Fтабл = 6,6 > Fфакт, = 0,05. Следовательно, принимается гипотеза Н0о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений. Пример 2 По территориям региона приводятся данные за 199Х г. (табл. 1.6). Таблица 1.6
Требуется: 1. Построить линейное уравнение парной регрессии у от х. 2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. 3. Оценить статистическую значимость параметров регрессии и корреляции. 4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимумах, составляющем 107% от среднего уровня. 5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. Решение 1. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу (табл. 1.7). Таблица 1.7
 , 155,8 + 0,9285,6 = 77,0.Получено уравнение регрессии: = 77,0 + 0,92х.С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб. 2. Тесноту линейной связи оценит коэффициент корреляции:  ;  = 0.52.Это означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х - среднедушевого прожиточного минимума. Качество модели определяет средняя ошибка аппроксимации:  = 5.7%.Качество построенной модели оценивается как хорошее, так как не превышает 8 - 10%.3. Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента и путем расчета доверительного интервала каждого из показателей. Выдвигаем гипотезу H0 о статистически незначимом отличии показателей от нуля: а = b =  = 0.tтабл для числа степеней свободы df = n - 2 = 12 - 2 = 10 и = 0,05 составит 2,23. Определим случайные ошибки та, тb,  : = 24,3;  = 0.281; = 0.219.Тогда  = 3.2;  = 3.3;  = 3.3.Фактические значения t-статистики превосходят табличные значения:  = 3,2 > tтабл = 2.3;  = 3,3 > tтабл = 2.3;  = 3,3 > tтабл = 2.3,поэтому гипотеза Н0 отклоняется, т.е. а, b и  , не случайно отличаются от нуля, а статистически значимы.Рассчитаем доверительный интервал для а и b. Для этого определим предельную ошибку для каждого показателя: a = 2,23 * 24,3 = 54; b = 2,23 * 0,281 = 0,62. Доверительные интервалы:  ; = 77 - 54 = 23; = 77 + 54 = 131; ; = 0.92 - 0.62 = 0.30; = 0.92 + 0.62 = 1.51.Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью р = 1 - = 0,95 параметры а и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля. 4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: хр =  * 1,07 = 85,6 * 1,07 = 91,6 тыс. руб., тогда прогнозное значение прожиточного минимума составит: = 77 + 0,92 * 91,6 =161 тыс. руб.5. Ошибка прогноза составит:  = 13,2 тыс. руб.Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:  = tтабл* = 2,23 * 13,2 =29,4.Доверительный интервал прогноза:  = 91,6 ±29,4; = 91,6-29,4 = 62,2 руб.; = 91.6+29,4 = 121 руб.Выполненный прогноз среднемесячной заработной платы оказался надежным (р = 1 - = 1 - 0,05 = 0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала Dyсоставляет 1,95 раза: 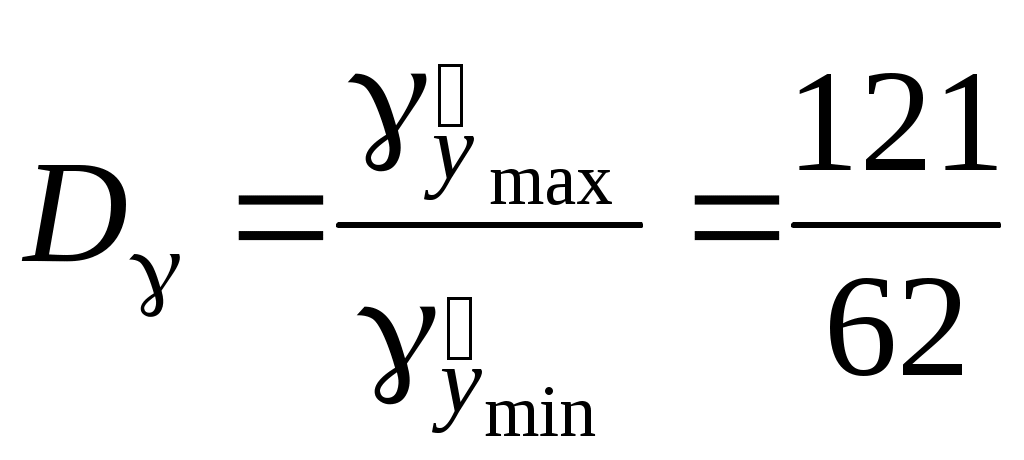 = 1,95.Пример 3 По группе предприятий, производящих однородную продукцию, известно, как зависит себестоимость единицы продукции у от факторов, приведенных в табл. 1.8. Таблица 1.8
Требуется: 1. Определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат. 2. Ранжировать факторы по силе влияния. Решение 1. Для уравнения равносторонней гиперболы  = 0,62 +58,74 *  : .Для уравнения прямой  = 9,30 + 9,83 *х2: Для уравнения степенной зависимости  = 11.75 +  : .Для уравнения показательной зависимости  = 14,87 +1,016 : .2. Сравнивая значения  , ранжируем хj, по силе их влияния на себестоимость единицы продукции:а)  = 1,63 %; в)  = 0,59%;б)  = -0,973%; г)  = 0,42%.Для формирования уровня себестоимости продукции группы предприятий первоочередное значение имеют цены на энергоносители; в гораздо меньшей степени влияют трудоемкость продукции и отчисляемая часть прибыли. Фактором снижения себестоимости выступает размер производства: с ростом его на 1% себестоимость единицы продукции снижается на -0,97%. Пример 4 Зависимость потребления продукта А от среднедушевого дохода по данным 20 семей характеризуется следующим образом: уравнение регрессии  = 2 * х0.3;индекс корреляции = 0,9;остаточная дисперсия  = 0.06.Требуется: Провести дисперсионный анализ полученных результатов. Решение Результаты дисперсионного анализа приведены в табл. 1.9. Таблица 1.9
 ; ; ; .В силу того что Fфакт = 76,7 > Fтабл = 4,4, гипотеза о случайности различий факторной и остаточной дисперсий отклоняется. Эти различия существенны, статистически значимы, уравнение надежно, значимо, показатель тесноты связи надежен и отражает устойчивую зависимость потребления продукта А от среднедушевого дохода. |
= 0.62+58.47*
= 2.64
= 9.30+9.83*x2
= 1.38
= 11.75+
= 1.503
= 26.3