Методика преподования математики. Предисловие рецензенты доктор педагогических наук, профессор Н. М. Назарова кандидат педагогических наук В. В. Эк Перова М. Н
 Скачать 4.24 Mb. Скачать 4.24 Mb.
|
493
345
36Т
ТЗТ
7
975
18 |
При решении примеров вида в) рассуждения проводятся т|| «120=100+20, 430+100=530, 530+20=550», т. е. этот случ( сложения (вычитания) сводится к уже известным учащимся с/ чаям сложения (вычитания) а), б).
4. Сложение трехзначных чисел с однозначным, двузначным | трехзначным без перехода через разряд и соответствующие сл\ чаи вычитания:
| а) 540+5 543+2 | 545-5 545-2 | б) 545+40 585-40 | в) 350+23 356+23 | 373-23 379-23 |
| г) 350+123 | 673-123 | | | |
| 356+123 | 679-123 | | | |
Выполнение действий производится устно. Учащиеся при выпол« нении действий пользуются теми же приемами, какими они пользо^ вались при изучении действий сложения и вычитания в пределах! 100, т. е. раскладывают второй компонент действия (второе слагав-; мое или вычитаемое) на разрядные единицы и последовательно их] складывают или вычитают из первого компонента.
Например:
6
350+123
73-123
1
123=100+20+3 673-100=573 573- 20=553 553- 3=550
23=100+20+3 350+100=450 450+ 20=470 470+ 3=473
5. Особые случаи сложения и вычитания. К ним относятся 1 случаи, которые вызывают наибольшие трудности и в которых ] чаще всего допускаются ошибки. Учащихся больше всего затрудняют действия с нулем (нуль находится в середине числа или в конце). Случай с числами, содержащими нуль, не требует особых приемов. Но таких примеров надо решать больше, повторить перед решением таких примеров решение примеров на сложение и вычитание, когда компонентом действия является нуль: 0+3, 5+0, 5-5:
а) 308+121 б) 402-201 в) 736-504
308+100=408 402-200=202 736-500=236
408+ 20=428 202- 1=201 236- 4=232
428+ 1=429
г) 0+436 700-0 725-725
х'стные приемы вычислений требуют от учащихся постоянного шза чисел по их десятичному составу, понимания места ры в числе, понимания того, что действия можно производить ко над одноименными разрядами. Не всем учащимся вспомо-льной школы это становится понятным одновременно. 11еред выполнением действий необходимо добиваться от уча-|||ц\ся предварительного анализа десятичного состава чисел. Учи-и- п. чаще должен ставить вопросы: «С чего надо начинать сложе-|пм"> Какие разряды складываем?»
15 противном случае учащиеся допускают ошибки при вычислениях. Они складывают десятки с сотнями, а результат записывают "|Ц)0 в разряд сотен, либо в разряд десятков, например: 100+10=500, 30+400=70, 30+400=470, 30+400=340, (./0+2=690, 670-3=640.
Эти ошибки свидетельствуют о непонимании позиционного значения цифр в числе, о неумении самостоятельно контролировать результаты действий. Учителю необходимо добиваться того, чтобы учащиеся проверяли выполнение действий, причем делали это не формально, а по существу. Нередко приходится наблюдать, что ученик якобы и сделал проверку, но выполнил ее формально. Он написал только обратное действие, а не решал, поэтому и не заметил допущенной ошибки, например: 490—280=110. Проверка. 110+280=490.
Нередко можно столкнуться с непониманием умственно отсталыми школьниками (даже старших классов) сущности проверки. Проверка часто выполняется учениками только потому, что этого либо требует учитель, либо такое задание содержится в учебнике. Часто при выполнении проверки ученик получает несоответствие между полученным результатом и заданным примером, но это не служит ему поводом для исправления неверного ответа, например: 570-150=320. Проверка. 320+150=470.
В данном случае проверка выступает как самостоятельное действие, никак не связанное с тем, которое ученик проверяет.
Учитель постоянно должен помнить об этих ошибках школьников с нарушением интеллекта и требовать ответа на вопросы: «Что показала проверка? Верно ли решен пример? Как доказать, что действие выполнено верно?»
Осознанному выполнению устных вычислений, выработке обобщенных способов выполнения действий служит постоянное внима-
194
195
ние к вопросам сравнения и сопоставления разных по трудно случаев сложения, вычитания. Важно научить учащихся вид| общее и особенное в тех примерах, которые они решают.
Например, сравнить примеры и объяснить их решение:
30+5, 300+40, 300+45, 300+140, 300+145, 300+105.
305-5, 340-40, 345-45, 340-300, 345-300, 345-200.
Полезно и составление учащимися примеров, аналогичных (г хожих) данным, или примеров определенного вида: «Составьт! пример, в котором надо сложить круглые сотни с единицами»;! «Составьте пример на вычитание, в котором уменьшаемое — | трехзначное число, а вычитаемое — круглые десятки» и т. д.1
Для закрепления действий сложения и вычитания в предела» 1000 приемами устных вычислений полезно решение примеров с| неизвестными компонентами.
II. Сложение и вычитание с переходом через) разряд.
Сложение и вычитание с переходом через разряд — это наибо«| лее трудный материал. Поэтому учащиеся выполняют действия столбик. Сложение и вычитание в столбик производятся над каж-| дым разрядом в отдельности и сводятся к сложению и вычитании в пределах 20. Но в этом случае возникают у умственно отсталь школьников трудности в записи чисел, т. е. в умении правильно подписать разряд под соответствующим разрядом.
Часто из-за неумения организовать внимание, из-за недостаточно четкого понимания позиционного значения цифр в числе, а то и из-за небрежности при записи цифр ученики сдвигают число, которое нужно прибавить или вычесть, влево или вправо и поэтому допуска-; ют ошибки в вычислениях. Особенно много ошибок учащиеся допускают при записи чисел в столбик, если действие производится над трехзначным и двузначным или однозначным числом. В этом случае десятки подписываются под сотнями, единицы под сотнями или десятками. Это приводит к ошибкам в вычислениях.
Например:
375 375 238
+ 6 +38
246 26ТГ
Много ошибок допускается в результате того, что ученики
убывают прибавить получившийся в уме десяток или сотню, а
Также забывают, что «занимали» сотню или десяток. Например:
. 178 345
124
"218
О
| 600 "283 32Т 710 345 -275- | 600 "283 -42Т |
собенно трудны случаи, при решении которых: 1) переход через разряд происходит в двух разрядах; 2) получается нуль в одном из разрядов; 3) содержится нуль в уменьшаемом; 4) в середине уменьшаемого стоит единица. Например:
"
375 228
-"• з •? к КПП
5
375 + 228
46
710 710
—^ту^- —тге- или
Нередко при вычитании можно встретить и такую ошибку: вместо того чтобы «занять» единицу высшего разряда, раздробить ее, ученик начинает вычитать из большей цифры вычитаемого меньшую цифру соответствующего разряда уменьшаемого. Например:"
375 529
^ 8
| Например: | | | | |
| 10 | 1010 | .1010 | 10 | 101010 |
| 375 | 375 | 805 | 805 | 1000 |
| 146 | 186 | 37 | 34 | 148 |
| 229" | Г39 | Т68 | 771 | 832 |
Особого внимания заслуживает решение примеров вида 800— —236, 810—236, 810—206. Следует сопоставить сначала 1-й и 2-й, а потом 2-й и 3-й примеры, особенности их решения, объяснить, в чем их различие, почему получаются разные ответы.
2) сложение и вычитание с переходом через разряд в двуй
разрядах (единиц и десятков): 375+486, 375-186, 286+58, 375-™
-86;
3) особые случаи сложения и вычитания, когда в сумме или в
разности получается один или два нуля, когда в уменьшаемом
содержится один или два нуля, когда в уменьшаемом содержатся
нуль и единица:
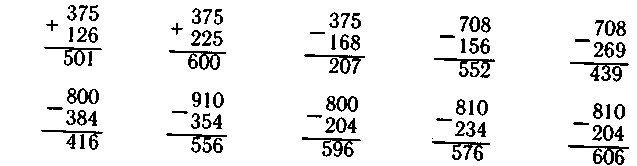
4) вычитание трехзначных, двузначных и однозначных чисел из 1000: 1000-375, 1000-75, 1000-5.
При объяснении решения примеров с переходом через разряд, учитывая, что умственно отсталые школьники при сложении забывают прибавлять то число, которое надо запомнить, можно разрешать надписывать это число над соответствующим разрядом.
Например:
1
+ 375
118
вождаться операциями с наглядными пособиями и дидактичес|| материалом.
Покажем объяснение умножения, а потом деления.
Например, надо 200-2. Рассуждаем так: 200 — это 2 соТ|
Возьмем 2 сотни палочек и еще 2 сотни палочек. Будет 4 сот!
или 400. Запишем: 2 сот.-2=4 сот.=400, 200-2=400. ?,
При делении 200:2 рассуждаем так: 200 — это 2 сотни. Воз! мем 2 сотни палочек. Если разделить их на две равные части, -т в каждой части получится по одной сотне, или по 100 единим Запишем: 2 сот.:2=1 сот. = 100, 200:2=100. Полезно сопоставим, умножение и деление единиц, десятков и сотен:
ц итков). Делим 18 десятков на 3. Получим 6 десятков, или 60. щишем: 18 дес. :3=6 дес. =60, 180:3=60». Процесс деления ;но показать и на палочках, и на брусках. Сначала учащиеся г. подробную запись, заменяя единицы десятками, затем запись _!ртывается. От учащихся требуется лишь устное объяснение. [яконец, свертывается и объяснение. Учащиеся записывают лишь
т.
Такое же объяснение проводится и при знакомстве с умножением и делением круглых десятков на однозначное число. Решети- подобных случаев сводится к внетабличному умножению и |и чению. Поэтому приведем лишь подробную запись решения:
3-3= 9
30-3= 90
300-3=900
8:4= 2
80:4= 20
800:4=200
120-4=?
12 дес. -4 дес.=48 дес.=480 120-4=480
480:4=?
48 дес.:4= 12 дес.= 120 480:4=120
3. Умножение и деление трехзначных чисел на однозначные без перехода через разряд (123x3, 486:2).
Решение таких примеров подготовлено рассмотрением всех предыдущих случаев умножения и деления. Успех выполнения действий здесь зависит от умения учащихся раскладывать числа на разрядные слагаемые. Поэтому предварительно полезны упражнения вида 253=200+50+3, 300+60+4=364.
Рассуждения проводятся так:
Такая развернутая запись постепенно свертывается:
1) 123-3=369 2) 123-3=369 3) 123-3=369
Рассуждения проводятся устно.
Аналогичное свертывание записи происходит и при делении.
Действия умножения и деления надо сопоставлять, проверяя каждое обратным действием: 400x2=800, 800:2=400.
2. Умножение и деление круглых десятков на однозначное число.
а) Рассматриваются случаи умножения и деления круглых де
сятков, которые сводятся к табличному умножению и делению:
60-3, 180:3. |
б) Рассматриваются случаи, которые сводятся к внетабличному|
умножению и делению без перехода через разряд: 120-3, 480:4.
Перед умножением и делением круглых десятков с учащимися необходимо повторить табличное и внетабличное умножение и деление (4-6, 24-2, 36:6, 36:3), а также определение общего количества десятков в числе («Сколько всего десятков в числе 120, 180, 360, 720?») и количества единиц в десятках («7 десятков. Сколько это единиц?»; «Сколько единиц з 2 десятках? 5 десятках? 10 десятках? 52 десятках?»).
При объяснении проводятся следующие рассуждения: «60-3=? 60 — это 6 десятков, 6 дес.-3=18 дес. 18 десятков — это 180, значит, 60-3=180». Можно показать учащимся на брусках арифметического ящика, пучках палочек, связанных десятками, что результат будет тот же. Для этого учитель берет по 6 брусков 3 раза. Получает 18 брусков, или 18 десятков. Это число 180.
При знакомстве с делением ход рассуждения аналогичен: «180:3=? Узнаем, сколько десятков содержится в числе 180 (18 200
123-3=?
123 = 100+20+3 100-3=300 20-3= 60 3-3= 9 300+60+9=369
123=100+20+3 100-3=300 20-3= 60 3-3= 9 300+60+9=369
486:2 = ?
486=400+80+6 400:2=200 80:2= 40 6:2= 3 200+40+3=243
100-3=300 20-3= 60 3-3= 9 300+60+9=369
201
4. Умножение 10 и 100, умножение на 10 и 100.
В пределах 1000 рассматривается умножение однозначного двузначного числа на 10 и 100 и соответствующие случаи дел* ния:
8-100=800
8- 10= 80
80- 10=800
| 10- 3 | 3- 10 | 80: 10 |
| 100- 8 | 8-100 | 800:100 |
| 25-100 | Ю- 25 | 250: 10 |
Умножение числа 10 учитель объясняет, опираясь на понятии умножения как сложения равных чисел.
10-3=10+10+10=30 10-3=30
10-5=10+10+10+10+10=50 10-5=50
Рассматривается еще несколько примеров. Сравниваются отве ты. Учащиеся убеждаются, что при умножении числа 10 на любой множитель к нему справа приписывается нуль.
Затем решаются примеры на умножение однозначного числа ня 10. Решение примера 3x10=? также производится приемом заме ны умножения сложением одинаковых слагаемых:
3-10=3+3+3. . .+3=30 10 раз
1 Можно использовать и переместительный закон умножения: \
10-3=30 3-10=30
Рассмотрев ряд таких примеров, сопоставив произведения и первый множитель, учащиеся приходят к выводу: чтобы умножить число на 10, нужно к первому множителю приписать справа один нуль.
Это правило умножения числа на 10 распространяется и на умножение двузначных чисел (25x10=250).
При умножении на 100 множитель 100 рассматривается как произведение двух чисел: 100=10* 10. Учащиеся практически знакомятся с использованием сочетательного закона умножения, хотя этот закон они не называют и не формулируют. Учитель объясняет: «Чтобы число умножить на 100, его нужно умножить сначала на 10, .. потом произведение умножить еще раз на 10, так как 100=10.10».
202
Затем запись дается в строчку: 6-100=6-10 • 10=600.
Решается также подробно еще несколько примеров. При реше-«и каждого примера учитель просит сравнивать произведение и !рвый множитель. Учащиеся самостоятельно приходят к выводу: •обы умножить число на 100, к нему нужно приписать справа а нуля.
Умножение 100 на однозначное число выполняется путем ис-
пьзования переместительного закона умножения:
100x5=?
5x100=500
5. Целение на 10 и 100.
Деление на 10, как показывает опыт, лучше усваивается учащимися при сопоставлении с действием умножения. Деление на 10 рассматривается как деление по содержанию:
2-10=20, отсюда 20:10=2.
20:10=2 сопровождается вопросом: «Сколько раз в двух десятках содержится один десяток?»
Как и в умножении, решается несколько примеров на деление на 10, сравниваются частное и делимое. Учащиеся убеждаются, [• что в частном получается делимое без одного нуля, и делают вывод:
чтобы разделить число на 10, в нем надо отбросить нуль справа. Этот вывод распространяется и на деление круглых сотен и десятков на 10 (400:10=40, 250:10=25).
Аналогично учащиеся знакомятся с делением на 100: 400:100=? 4-100=400 400:100=4
Деление на 100 можно объяснить и последовательным делением на 10 и еще раз на 10:
4
400:100= 4
400: 10=40
40: 10= 4
00:100=400:10:10=4
Деление на 10 и 100 учащиеся учатся производить как без остатка, так и с остатком: 40:10=4, 45:10=4 (ост. 5).
203


