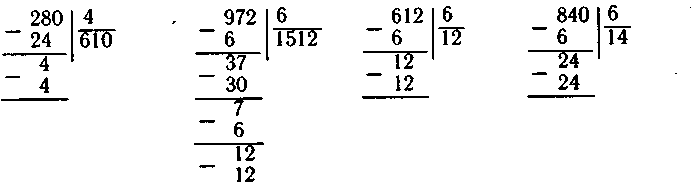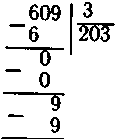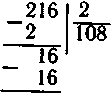|
|
Методика преподования математики. Предисловие рецензенты доктор педагогических наук, профессор Н. М. Назарова кандидат педагогических наук В. В. Эк Перова М. Н
10-4 100-4
40:4 400:4
0: 10 400: 10 400:100
Необходимо также сравнить умножение на 10 и 100 с умнонв
нием на 1 и 0, деление на 10, 100 с делением на 1. Это позвол!
каждый раз анализировать выражения, прежде чем приступать!
выполнению действия. ••
Закреплению действия способствует также кратное сравнение! чисел (во сколько раз одно число больше или меньше другого).; Например, даются такие задания: «Во сколько раз 2 меньше, чем/ 20, 200?»; «Во сколько раз 300 больше, чем 3, 10, 100?» Пример 300:3=100 можно прочитать так: «Число 300 больше, чем 3, в 100 раз». Или: «Число 3 меньше, чем 300, в 100 раз». «Какими действиями можно сравнить числа 400 и 10?» — спрашивает учитель. Ученики отвечают: «Сравнить эти числа можно действиями деления и вычитания: 400:10, 400—10». Учащиеся учатся самостоятельно ставить вопросы: «На сколько число 400 больше 10?»; «Во сколько раз 400 больше 10?»
II. Письменное умножение и деление в пределах 1000.
Умножение и деление на однозначное число с переходом через разряд.
Этот вид умножения и деления представляет наибольшие трудности для учащихся. Умножение и деление с переходом через разряд выполняется приемами письменных вычислений. Учащиеся при этом впервые знакомятся с алгоритмом письменного умножения и деления. Поэтому, так же как при сложении и вычитании, следует познакомить учащихся с записью действий в столбик на самых легких случаях умножения (нет перехода через разряд) и деления (каждый разряд делимого без остатка делится на дели-| 204
. Затем следует расположить материал по нарастающей сте-трудности в такой последовательности:
шожение
Умножение двузначного числа на однозначное с переходом |м'з разряд в разряде десятков или единиц (27x3, 74x2).
Умножение двузначного числа на однозначное с переходом
срез разряд в разряде единиц и десятков (85x3).
Умножение трехзначного числа на однозначное с переходом
|срез разряд в одном разряде — единиц или десятков (127x3,
54x2).
Умножение трехзначного числа на однозначное с переходом
|ерез разряд в двух разрядах — единиц и десятков (175x3).
Особые случаи умножения — первый множитель — трех-
жачное число с нулем на конце или в середине (280x3, 208x3).
6. Умножение двузначного числа на круглые десятки (27x20).
I Знакомство с новой записью умножения в столбик, как уже
I было сказано выше, целесообразно показать на самых легких при
мерах, в которых сам процесс вычислений не представляет для
учащихся никаких трудностей и все внимание должно быть сосре
доточено на новой форме записи примера, например: 123x3. Сна
чала учащимся предлагается решить этот пример устно. Затем
учитель знакомит учащихся с записью этого примера в столбик и
его решением. Рассуждение проводится так: «Запишем первый
множитель 123. Второй множитель — однозначное число, которое
состоит из единиц, поэтому множитель подписываем под единица
ми первого множителя. Проводим черту, слева ставим знак умно
жения и начинаем умножать с единиц. 3 единицы умножим на 3,
получим 9 единиц; подписываем их под единицами. Умножим 2
десятка на 3, получим 6 десятков; подпишем их под десятками.
Умножаем сотни, 1 сотню умножим на 3, получим 3 сотни; подпи
сываем 3 сотни под сотнями. Произведение равно 369».
Решается несколько аналогичных примеров. Особое внимание учащихся надо обратить на последовательность умножения и правильность записи произведения. Нужно помнить о том, что по аналогии с устными приемами вычислений учащиеся начинают умножение не с единиц, а с сотен, а результат умножения подписывают под единицами. Поэтому на первых порах запись множителей и произведения целесообразно давать в три цвета (единицы — одним цветом, десятки — другим, сотни —третьим).
205
При решении примеров на умножение с переходом через ряд трудность вызывает не только запись примеров, но и процесс вычислений. Учащиеся забывают прибавить число, Ки™ рое они держали в уме, забывают, сколько надо прибавить. | этом случае учащимся можно разрешить записывать числа, ко<1 рые нужно запомнить, на отдельном листочке — черновике (( должен быть в тетради каждого ученика класса).
Особое внимание нужно уделить решению примеров с пере) дом через разряд в двух разрядах.
Эти примеры наиболее трудны, поэтому их необходимо
больше. -ч
Умножение трехзначных чисел с нулем на конце или в серели не требует особо пристального внимания, так как учащихся -л,\ трудняет умножение нуля: они путают его со сложением с нулем. Поэтому предварительно надо повторить умножение нуля и нуль (0x3, 5x0).

П
280
ри умножении чисел, оканчивающихся нулем, учитель вспомогательной школы использует различные формы Записи. В одних случаях множитель подписывается под нулем, в других — под первой значащей цифрой:
,
X
280
При первой форме записи рассуждения проводятся так: «О единиц умножаем на 3, получается 0, подписываем 0 под еди-, ницами. 8 десятков умножаем на 3, получаем 24 десятка. 4 десяти ка записываем под десятками, а 2 сотни запоминаем. 2 сотни! умножаем на 3, получаем б сотен, прибавляем к ним 2 сотниЛ получаем 8 сотен, 8 сотен подписываем под сотнями. Произведение равно 840».
При второй форме записи рассуждения проводятся так: «В числе 280 содержится 0 единиц; при умножении 0 на любое число получается 0, поэтому начинаем умножать сразу десятки; 8 десятков умножаем на 3, получаем 24 десятка. 4 десятка записываем под десятками, а 2 сотни запоминаем, 2 сотни умножаем на 3, получаем 6 сотен, прибавляем еще 2 сотни, получаем 8 сотен, 8 206
рп записываем под сотнями. О единиц сносим. Произведение Но 840».
1ри второй форме записи нужно время от времени спрашивать цихся, почему нуль сносится в произведение. В противном чае учащиеся делают эту операцию механически. Учащихся следует познакомить только с одной формой записи.
I Умножение на круглые десятки
В

пределах 1000 рассматриваются случаи умножения двузнач-вЫх чисел на круглые десятки. Учитывая то, что учащиеся уже .шакомы с приемами письменных вычислений, умножение на круг-1' десятки выполняется письменно. Это облегчает процесс вычисления. Запись умножения двузначного числа на двузначное число надо объяснить подробно, показав аналогию с записью чисел в столбик при сложении и вычитании (единицы и десятки множителей подписываются соответственно друг под дру-гом, и умножение начинается с единиц).
Для слабоуспевающих по математике учащихся эта запись может оставаться единственной. Остальных учащихся по усмотрению учителя можно познакомить с более свернутой формой записи примеров такого вида, при которой умножение на нуль не производят, например 27 • 20:
х27
* 20
т. е. нуль второго множителя не подписывается под значащей цифрой. Производится умножение первого множителя на два, т. е. на число круглых десятков, а потом полученное произведение умножается на 10, т. е. приписывается к нему нуль справа.
Такая операция может быть понятна учащимся только в том случае, если будет проведена подготовительная работа. Перед умножением на круглые десятки устно следует повторить случаи вида 2x2x10, 2x20 и сравнить ответы этих примеров, объяснить, почему произведения равны. Учащиеся убеждаются, что второй множитель — круглый десяток (20, 30, ..., 90) — можно разложить на два множчтзля: на число десятков и 10. Сначала умножаем множитель на число десятков, а потом на 10. Затем надо порешать примеры на умножение двузначного числа на 10 (27x10, 38x10 и т. д.).
207
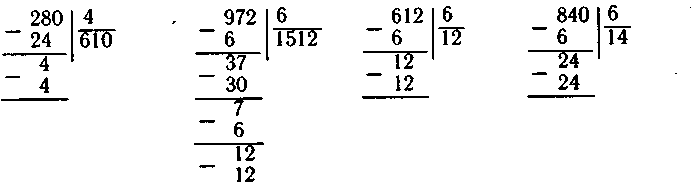
Решать примеры вида 27x20 следует устно. Объяснение vнадо давать так, чтобы учащиеся поняли, почему умножаем I число десятков, а нуль приписываем к полученному произведении справа. Рассуждения проводятся так: «20 можно записать кэ!> произведение, т. е. 20=2x10, 27-20=27-2-10=54-10=540».
Запишем решение этого поимеоа в столбик-
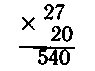
Сначала 27 умножим на 2, получим 54, а потом произведение 54 умножим на 10, т. е. припишем к нему 0 справа.
На первых порах учащиеся при решении этих примеров долж ны давать подробные объяснения. Затем рассуждения постепенно свертываются, но иногда следует задавать учащимся вопросы: «Почему при умножении на круглые десятки приписываем 0 справа? В виде произведения каких двух чисел можно записать второй множитель? На какое число сначала умножали первый множитель? На какое число потом умножали полученное произведение?» Эти вопросы позволяют учащимся более сознательно подходить к процессу выполнения умножения на круглые десятки. Кроме того, они готовят почву для сознательного выполнения умножения чисел на круглые сотни и тысячи.
Деление
Деление изучается в такой последовательности: I
1) число сотен, десятков и единиц делится без остатка на:
делитель (369:3);
число сотен делится на делитель без остатка, а число десят
ков без остатка на делитель не делится (372:3);
число сотен не делится без остатка на делитель (570:3);
число сотен делимого меньше числа единиц делителя, в
частном получается двузначное число (153:3);
особые случаи деления, когда в частном на конце или в
середине получается нуль (720:3, 812:4, 820:4);
деление на круглые десятки.
Деление трехзначного числа на однозначное, когда сотни, десятки и единицы нацело делятся на делитель, учащиеся выполняют устно: 369:3=123. Однако на примере такого вида следует познакомить учащихся с новой формой записи деления в столбик. Рассуждения проводятся так: «Сначала записываем делимое. Знак деления обозначаем прямым углом, одна из сторон которого не-208
о сколько продолжена вниз. Внутри угла записываем У2"з
делитель. Деление начинаем с сотен (с высшего разряда). Частное от деления каждого разряда записываем под делителем. 3 сотни делим на 3, получаем 1 сотню, записываем ее в частное. Проверяем, все ли сотни разделили. 1 сотню умножаем на 3 и пишем под сотнями. Ставим знак «минус» (сотни вычитаем). (Сносим 6 десятков и делим их на 3. И т. д. Частное 123».
Действие деления наиболее трудно для учащихся. Особенно труд-
|ны те случаи деления, в которых один или два разряда нацело не делятся на делитель, или случаи, в которых в частном получается нуль в середине. Умственно отсталые школьники допускают нередко ошибки, связанные с неправильным подбором числа в частном, — их не смущает, что при вычитании в остатке получается число, делящееся на делитель или больше делителя. Учащихся не смущает и то, что число, получившееся в частном, больше делимого.
Нередко в частном получается число, имеющее большее число знаков, чем делимое. Причинами таких ошибок опять являются неправильный выбор частного, получающийся больше делимого (или равный делителю) остаток. Например:
Для того чтобы предотвратить подобные ошибки в вычислениях и помочь учащимся овладеть трудным для них действием деления, необходимо задолго до знакомства с приемами письменного деления провести подготовительную работу:
Постоянно, на каждом уроке повторять таблицу умножения
и деления.
Решать примеры на деление с остатком: 15:2=7 (ост. 1);
21:4=5 (ост. 1); 61:6= ; 82:2= и т. д., обращая внимание на
то, что остаток должен быть всегда меньше делителя. Подбор,
цифр частного, например 24:5, следует производить постепенно:
24 на 5 не делится, делим 23, потом 22, 21, наконец, 20.
С самого начала знакомства с делением в столбик надо учить детей прикидке ответа, умению сразу определять, сколько цифр должно получиться в ответе.
209
Например, если делится трехзначное число на однозначное, и число сотен делимого больше делителя или равно ему, то в част ном получатся сотни. Сотни стоят в числе на третьем место Значит, в ответе должно получиться трехзначное число. Можно рекомендовать в частном поставить сразу три точки, например:
972
Если в трехзначном числе число сотен меньше делителя, то сотни надо раздробить в десятки, прибавить десятки делимого и начинать деление. В этом случае в частном получится двузначное число, так как десятки стоят на втором месте. В частном 148 3 учащиеся ставят две точки. Предварительная прикидка количества цифр в числе предотвращает возможность пропуска нуля в частном или его недописывание. Особое внимание уделяется решению примеров, когда среди цифр частного получается нуль:
2
609:3=203

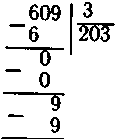
Когда учащиеся усвоят алгоритм деления, можно познакомить их с сокращенной записью.
16:2=108
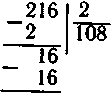
Действие деления проверяется умножением. Решаются сложные примеры на все четыре арифметических действия и на порядок действий.
Деление на круглые десятки
Предварительным материалом к данной теме является решение примеров вида 80:20, 120:20, в которых учащиеся деление производят как деление по содержанию 8 дес.:2 дес.=4 (раза), 12 дес.:2 дес.=6. На основании решения таких примеров учащие-210
{Я убеждаются, что если делимое и делитель оканчиваются нуля-ИИ, то частное легче получить, если деление выполнять, не обращая внимания на нули, т. е. мысленно отбросить (120:20=6). При этом обращается внимание учащихся на то, что, отбрасывая пуль в делимом, мы его делим на 10.
З
720 60
атем учащиеся знакомятся с делением трехзначно-30 го числа на двузначное, используя алгоритм письмен-"24" ного деления: делим 72 десятка на 3 десятка. От учащихся необходимо требовать проверки действия деле-120 ния умножением.
Для закрепления действий, выработки прочных навыков вычислений и повторения теоретических знаний решаются примеры на нахождение неизвестных компонентов действия, порядок действий.
Вопросы и задания
Подготовьте сообщение на тему «Особенности и трудности усвоения
нумерации многозначных чисел».
Составьте схему последовательности изучения нумерации первой тыся
чи.
Составьте фрагмент урока на одну из тем: «Нумерация круглых сотен»,
«Устная нумерация трехзначных чисел», «Письменная нумерация трехзнач
ных чисел». Изготовьте наглядные пособия к этим урокам.
Составьте примеры на сложение и вычитание с возрастающей степе
нью трудности.
Какие трудности испытывают учащиеся при решении примеров вида
814—208, 346—149? Каковы пути преодоления этих трудностей?
Раскройте систему и методику ознакомления с алгоритмами письмен
ного умножения и деления.
Глава 13 МЕТОДИКА ИЗУЧЕНИЯ МНОГОЗНАЧНЫХ ЧИСЕЛ
ОБУЧЕНИЕ НУМЕРАЦИИ МНОГОЗНАЧНЫХ ЧИСЕЛ
При изучении данного раздела можно выделить следующие ступени:
знакомство с новыми счетными и разрядными единицами:
десятком тысяч, сотней тысяч, единицей миллионов;
счет до 1 млн уже известными счетными единицами и
новыми: десятками тысяч и сотнями тысяч;
выработка прочных навыков в записи чисел до 1 млн;
211
повторение класса единиц и знакомство с классом тысл
(1—2-е классы);
анализ многозначных чисел по десятичному составу — в!
деление в числе классов и разрядов, составление числа по данны
классам и разрядам.
Учащимся необходимо показать, где в практике, в жизни ж пользуются те многозначные числа, которые они изучают на ур< ках в школе.
Нумерация многозначных чисел усваивается умственно отстг лыми учащимися с большим трудом. Эти трудности связаны первую очередь с тем, что многозначное число трудно конкретизи ровать. Наглядные пособия, которые используются при изучении данной темы: абак, счеты, таблица разрядов и классов. Таблицы™ соотношения мер длины и мер массы являются условными пособиями. Они скорее конкретизируют не число, а десятичную систему счисления. Обобщенные понятия, которые используются для усвоения как устной, так и письменной нумерации, носят также условный и отвлеченный характер. К ним относятся понятия разряда, класса, поместного значения цифры в числе и др.
Учащиеся школы VIII вида испытывают затруднения в счете как простыми единицами, так и другими единицами счета (десятками, сотнями, единицами тысяч и др.). Когда надо сделать переход к новому разряду или классу (1299—1300, 2999—3000), ученик считает: две тысячи девятьсот девяносто десять и т. д. Как и раньше, при изучении чисел предыдущих концентров, наибольшие затруднения вызывает счет в обратном порядке и счет равными числовыми группами (по 25, 50, 200, 250, 500).
Наблюдаются также трудности при чтении многозначных чисел. На первых порах ученики не выделяют при чтении класса тысяч (например, число 4231 читают как 423 один или 42, 31, не учитывают нулей при чтении чисел (например, число 5620 читают как 562, 3085 читают как 385 или 3, 0, 85).
Не только чтение, но и выработка умений и навыков при письме многозначных чисел требует от учащихся значительных усилий, большого количества тренировочных упражнений. Учащиеся переставляют цифры местами, значит, испытывают трудности в усвоении позиционного значения цифр в числе, пропускают нули или вписывают лишние (например, число' 308 576 записывают как 38 576, число 38 000 записывают как 380 000, число 80 050 записывают как 80 500 и т. д.). 212
Нечеткое представление о разрядах, классах нередко затрудня-
|ет сравнение соседних разрядов и классов (например, 2, 20, 200, 2000; 5 и 5 тысяч; 60 и 60 тысяч), нахождение наибольшего и наименьшего числа каждого разряда.
Причем трудности, возникающие у учащихся при изучении темы «Нумерация многозначных чисел», неоднородны. Одни учащиеся довольно быстро усваивают устную нумерацию (счет и анализ чисел), но долго не могут постичь письменную нумерацию. Для других оказывается проще усвоение письменной нумерации, а последовательность счета, десятичный анализ чисел усваивается медленнее, с большим трудом.
Изучение нумерации многозначных чисел не должно ограничиваться только теми уроками, которые отводятся на первоначальное знакомство с этой темой. Упражнения на закрепление устной и письменной нумерации должны быть неотъемлемой частью почти каждого урока математики. Их следует включать в устный счет, арифметические диктанты. От сознательного усвоения нумерации зависит успех овладения арифметическими действиями.
В действующих учебных программах предлагается различная последовательность изучения нумерации многозначных чисел в школах VIII вида для учащихся с интеллектуальным недоразвитием.
В одних программах предлагается многозначные числа в пределах 1 000 000, т. е. все числа II класса тысяч, изучать не сразу, а сначала ознакомить учащихся с числами в пределах 10 000 (6-й класс), затем в пределах 100 000 (7-й класс), и, накрнец, в пределах 1 000 000 (8-й класс).
В других программах предлагается изучение сразу всего класса тысяч, т. е. всех чисел в пределах 1 000 000 в 6-м классе. Новая последовательность изучения многозначных чисел позволит, как показали специальные исследования Б. Б. Горскина, И. М. Шейной, быстрее сформировать обобщенное понимание сущности десятичной системы счисления, в которой при чтении и записи многозначных чисел важно уметь выделять классы, в каждом классе — три разряда (единицы, десятки, сотни). Более раннее ознакомление учащихся со всем классом многозначных чисел (6-й класс) в пределах 1 000 000 позволяет закреплять знания нумерации в течение длительного времени (6—8-е классы).
В данном учебнике мы предлагаем методику изучения многозначных чисел до 1 000 000, учитывая разную последовательность при изучении нумерации многозначных чисел.
|
|
|
 Скачать 4.24 Mb.
Скачать 4.24 Mb.