Методика преподования математики. Предисловие рецензенты доктор педагогических наук, профессор Н. М. Назарова кандидат педагогических наук В. В. Эк Перова М. Н
 Скачать 4.24 Mb. Скачать 4.24 Mb.
|
1 Изучение нумерации чисел 21—99 ' Изучение нумерации чисел от 21 до 99 лучше всего начать с |разования любого двузначного числа из десятков и единиц. |цдо показать общий принцип образования этих чисел. Например, или 2 десятка палочек и еще 5 палочек; 2 дес. см (2 дм) и еще см. Получили число двадцать пять. Числительные образуются из ух слов. Сначала произносятся десятки, а затем единицы. Это • к:ло откладывается на счетах. Так из десятков и единиц на шкретном счетном материале учащиеся должны научиться обра- .опывать любое двузначное число и называть его. Одновременно "ни учатся обозначать эти числа письменно с помощью цифр. Знакомство с письменной нумерацией лучше всего проводить с помощью абака. На абаке учитель просит отложить число (например, 21). Ученик анализирует это число. Оно состоит из двух десятков и одной единицы. В кармашки вставляются цифры, соответствующие числу десятков и единиц. Хорошим пособием являются и таблички с круглыми десятками, в которых нуль заставляется определенной цифрой, обозначающей число единиц. После того как учащиеся поймут общий принцип образования и записи двузначных чисел, необходимо поработать над образованием и записью чисел 21—99 и отработать последовательность чисел от 1 до 100. Например, к двум брускам (двум десяткам) добавляется один кубик (одна единица), получается число двадцать один, добавляется еще один кубик (одна единица), получается число двадцать два — это два бруска и два кубика. Два бруска и три кубика образуют число двадцать три и т. д. Два бруска и девять кубиков образуют число двадцать девять, а если прибавить еще один кубик, то получится два бруска и десять кубиков, 10 кубиков можно заменить одним бруском. Получилось 3 бруска — 3 десятка, или тридцать. Важно постоянно обращать внимание на образование каждого нового десятка. Например, после образования числа 99 прибавить еще 1 единицу (кубик) — получилось 9 десятков и 10 единиц. 10 единиц заменим одним десятком, получим 10 десятков, или сто. Очень важно и на пособиях, и на числах особое внимание обратить на образование нового десятка: . 29+1=2 дес. 9_ед.+!_ед.=2 дес. 10 ед.=3 дес. 30-1=2 дес. 10 ед.-1 ед.=2 дес. 9 ед.=29 99+1=9 дес. 9_е!ц.+1_ед.=9 дес. 10 ед. = 10 дес. = 100 100-1 = 10 дес.-1 ед.=9 дес. 10 ед. —1 ед.=9 дес. 9 ед.=99 149  Каждому ученику следует предложить просчитать по одному 1 до 100 и обратно, оперируя различными пособиями и без пос бий. Особое внимание рекомендуется обращать на счет от заданног до заданного числа с переходом через десяток (29, 30, 31] Можно также дать задания: «Считайте от 58 до 61, от 77 до 83 Считайте обратно: от 92 до 88, от 43 до 39». Так же как и при изучении чисел первого и второго десятка, не обходимо закрепить с учащимися свойства натурального ряд чисел: каждое число больше предыдущего и меньше последующей на единицу. Это только тогда становится ясным умственно отста лым школьникам, когда они не только называют числовой ряд I определенной последовательности, но и выполняют такие задания:
В этот период большое внимание уделяется десятичному анализу чисел (сначала с помощью пособий, а потом и без них). Учащиеся учатся составлять число из десятков и единиц, а также раскладывать его на десятки и единицы. Можно предложить такие задания: 1. Взять два пучка палочек и еще 5 палочек. Какое число получили? (То же самое задание выполняется на брусках и куби ках, полосках и квадратах.)
150
Учитель демонстрирует таблицу-квадрат (10x10) с десятью рядами чисел от 1 до 100:
Такие же квадраты могут начертить ученики в своих тетрадях и вписать в них числа от 1 до 100. Если в классе есть учащиеся, которые еще не усвоили место единиц и десятков в числе, то им лучше вписывать в квадраты числа двумя цветами: единицы — одним цветом, а десятки — другим. С помощью таблицы сравнивают: рядом стоящие числа в натуральном ряду («На сколько одно число больше или меньше другого?»); все числа одного ряда (число десятков постоянно, кроме последнего числа, а число единиц изменяется); числа между собой в столбцах (число десятков меняется, а число единиц неизменно). Каждое число в столбце можно сравнить с выше и ниже стоящим числом. Кроме того, целесообразно дать задания: прочитать столбец чисел, оканчивающихся цифрой 5, 7, 9, 0; объяснить, как образуются из чисел предпоследнего столбца числа последнего столбца — круглые десятки. При изучении нумерации в пределах 100 учащиеся знакомятся с разрядной таблицей. Учитель вводит новый термин «разряд», сообщая, что единицы относятся к первому разряду и пишутся в числе на первом месте справа, десятки — ко второму разряду и пишутся в числе на 151 I в 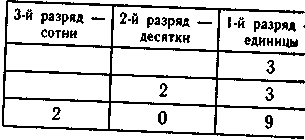 тором месте справа, а тором месте справа, асотни — к третьему разряду и пишутся в числе на третьем месте справа. После этого могут быть даны задания: назвать число, которое начинается с разряда десятков, с разряда сотен; сравнить числи 53 и 57, 61 и 41, 83 и 97, 1 и 51, 15 и 51. Сравнивать числа надо начинать с высших разрядов (если число десятков больше, то на единицы можно и не смотреть, так как все число будет больше 84<97, так как 8 дес.<9 дес.). Учащихся надо познакомить с различной формой записи числа Например, число 85 можно записать и так: 8 десятков и 5 единиц, или 80+5. Число 85 представлено в виде суммы разрядных ела гаемых (а можно из разрядных слагаемых составить число 80+5=85) 85=8 дес. 5 ед., 85=80+5, 80+5=85. Далее учащиеся знакомятся с четными и нечетными числами (числа, которые оканчиваются цифрами 2, 4, 6, 8, 0, четные; числа, которые оканчиваются цифрами 1, 3, 5, 7, 9, нечетные). Закрепляются и расширяются знания об однозначных и двузначных числах. Дети могут назвать не только наименьшее, но и наибольшее двузначное число. Счет ведется в пределах 100 равными числовыми группами по 2, 5, 10, 20 сначала на конкретном материале (числовые фигуры, арифметический ящик, счеты, монеты, масштабная линейка и др.), а затем отвлеченно в прямом и обратном порядке. Закреплению знания счета равными числовыми группами помогает работа с квадратом из 100 чисел (ученики считают и показывают числа, которые получаются от счета по 2, 5, 10, 20). Учащиеся всей предшествующей работой по нумерации чисел в пределах 100 подготовлены к тому, чтобы понять различие числа и цифры (всего 10 цифр — О, 1, 2, 3, 4, 5, 6, 7, 8, 9, а чисел очень много; с помощью этих 10 цифр можно обозначить любое число — цифра, стоящая в числе на первом месте справа, обозначает единицы, на втором — десятки, на третьем — сотни и т. д.). Естественно, что понятие числа и цифры усваивается не сразу всеми учащимися. Только ежедневная, кропотливая работа в течение длительного времени может дать положительные результаты. Для закрепления поместного значения цифр в числе могут быть проведены следующие упражнения: 1. Записать число 46. Сколько цифр в числе? Какие цифры? Что показывает цифра 6? Что означает цифра 4? 152 \1 Записать однозначное число (двузначное, трехзначное). Рлько цифр в этих числах? |3 С помощью цифр 3 и 5 записать два однозначных числа. Влько всего чисел можно записать этими цифрами? |С нумерацией сотни целесообразно связать изучение мер 4пы (метр разделить на сантиметры и дециметры) и стоимости 5ль разделить на копейки). |Для закрепления нумерации полезно выполнить действия сложе-и вычитания, причем приемы вычислений должны быть основана знании свойств натурального ряда чисел (24+1, 25—1), а ке на знании десятичного состава чисел (40+8, 48—8, 48—40). |Для решения случаев вида 24+1 и 25—1 наглядным пособием >1чно служит таблица с записью чисел от 1 до 100. (Чтобы результат прибавления к числу 1, надо в числовом ряду Йайти следующее за ним число, а чтобы узнать результат вычитания из числа 1 — предшествующее число.) Сначала при сложении и вычитании числа с единицей учащиеся опираются на числовой ряд. Затем этим пособием разрешается пользоваться лишь тем ученикам, которые еще нетвердо знают последовательность чисел. Постепенно всех учащихся надо переводить на решение примеров без использования пособия. При выполнении действий вида: 4 48- 8 48-40 0+ 8 8+40 проводится рассуждение: «40 — это 4 десятка (берем 4 бруска), прибавляем 8 единиц (8 кубиков). Получается 4 десятка и 8 единиц (4 бруска и 8 кубиков). Это число 48». Пример 8+40 решается не на пособиях, а путем использования переместительного закона сложения. «48—8=? 48 — это 40+8. Берем 4 бруска (4 десятка) и 8 кубиков (8 единиц). Убираем 8 кубиков (8 единиц). Остаются 4 бруска (4 десятка или 40)». Важно не только правильно решить примеры 40+8 и 8+40, но и сопоставить их, т. е. найти, в чем их сходство и в чем различие, почему ответ получится одинаковым. Примеры 48—8 и 48—40 также надо сравнить, причем не только компоненты, но и приемы вычисления (в первом примере вычитаем единицы, десятки не изменяются; во втором вычитаем десятки, единицы не изменяются). Сравниваем ответы. 153 СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 100 При обучении сложению и вычитанию в пределах 100 собл! ются все требования, которые предъявляются к обучению вьн нению действий в пределах 20. Многие трудности, которые испытывают школьники с нару нием интеллекта при выполнении действий сложения и вычита в пределах 20, не снимаются и при выполнении этих же деист! в пределах 100. Как показывают опыт и специальные йсследс ния по-прежнему большие затруднения учащиеся испытывают I выполнении действия вычитания. Наибольшее количество оши( возникает при решении примеров на сложение и вычитание переходом через разряд. Характерная ошибка при вычитании, единиц вычитаемого вычитают единицы уменьшаемого. Напримг, 35—17=22. Наблюдается также тенденция замены одного деж ' вия другим. Например: 64—16=80, 17+2=15 (вместо вычитании выполнено сложение и наоборот). При выполнении действий < двузначными числами учащиеся часто принимают во вниманш только единицы одного разряда, единицы другого разряда (первого или второго компонентов) переписывают без изменении (36+11=46, 85—24=64). Допускаются и такие ошибки: учащиеся складывают или вычитают, не обращая внимания на разряды: еди ницы складывают с десятками (37+2=57, 38—20=36), из меньше го числа вычитают большее (17—38=21), при решении сложных примеров выполняют только одно действие (12+14—8=26). Характерно, что учащиеся школы VIII вида долгое время не овладевают рациональными приемами вычисления, задерживаясь на приемах пересчитывания конкретных предметов, присчитывания по единице. Причины ошибок заключаются в недостаточно твердом знании таблиц сложения и вычитания в пределах 10 и 20 (39—7=31, 42+7=48), в недостаточно твердом знании и понимании позиционного значения цифр в числе или в неумении использовать свои знания на практике, а также в особенностях мышления школьников с интеллектуальным недоразвитием. Последовательность изучения действий сложения и вычитания обусловлена нарастанием степени трудности при рассмотрении различных случаев.
В+5 35-5=30 41-2=45 |В+30 3.5-20=5 47-32=47-30-2 5+26=30+20+6 56-20=5 47-42=47-40-2 86+30 56-26=56-20-6 47-27=47-20-7 145+2=40+5+2 145+32=45+30+2 р8. Сложение двузначного числа с однозначным, когда в сумме йучаются круглые десятки. Вычитание из круглых десятков Нозначного и двузначного числа: 4 35+5=30+5+5 5+35=30+5+5 35+45=35+40+5 0-5= 40-23=40-20-3 40-33=40-30-3 4. Сложение и вычитание с переходом через разряд. 3 42- 7 62-27 62-57 5+ 7 7+35 35+27 Г Все действия с примерами 1, 2 и 3-й групп выполняются прие-»ами устных вычислений, т. е. вычисления надо начинать с единиц высших разрядов (десятков). Запись примеров производится в строчку. Приемы вычислений основываются на знании учащимися нумерации, десятичного состава чисел, таблиц сложения и вычитания в пределах 10. Действия сложения и вычитания изучаются параллельно. Каждый случай сложения сопоставляется с соответствующим случаем вычитания, отмечается их сходство и различие. Такие случаи сложения, как 2+34, 5+45 и др., не рассматриваются самостоятельно, а решаются путем перестановки слагаемых и рассматриваются совместно с соответствующими случаями: 34+2, 45+5. Объяснение каждого нового случая сложения и вычитания проводится на наглядных пособиях и дидактическом материале, с которым работают все ученики класса. Рассмотрим приемы выполнения действий сложения и вычитания в пределах 100: 1) 30+20= 50-30= Рассуждения проводятся так: 30 — это 3 десятка (3 пучка палочек). 20 — это 2 десятка (2 пучка палочек). К 3 пучкам палочек прибавим 2 пучка, всего получили 5 пучков палочек, или 5 десятков. 5 десятков — это 50. Значит, 30+20=50. 155 Такие же рассуждения проводятся и при вычитании круг/и.г десятков. Подробная запись на первых порах позволяет закрепить пос и довательность рассуждений: 30+20=50 3 50-20=30 5 дес.-2 дес.=3 дес.= дес.+2 дес.=50 дес.=50 ,,._. _ ^^.—^ дс1..=ои К решению примеров привлекаются все пособия, которые и< пользуются при изучении нумерации. Действия производятся о6> зательно на счетах. 2) 30+26 26+30 „„ „„ О 56-30 бъяснение решения примеров данного вида проводится также на пособиях (абак, арифметический ящик, счеты). Полезно пока зать учащимся подробную запись выполнения действия: 3 56-30 26=20+ 6 30+20=50 50+ 6=56 0+26 56=50+ 6 50-30=20 20+ 6=26 или 30+26=30+20+6=50+6=56. Этой записью учитель пользуется только при объяснении. Ученикам же нужно показать короткую форму записи, но требовать устного комментирования при выполнении действий, при записи — подчеркивания десятков: Указанные выше случаи сложения, а также вычитания решаются ответственно одинаковыми приемами. Однако по трудности они не-•юзначны. Для школьника с нарушением интеллекта значительно 1уднее к меньшему числу прибавить большее. (2+7)-9—7 — это |иболее трудный случай табличного вычитания. Все это говорит о ом, что, соблюдая требование постепенности нарастания трудностей (фи решении примеров, необходимо учитывать не только приемы вы-(шслений, но и числа, над которыми выполняются действия. Объяснение: «В числе 45 — 4 десятка и 5 единиц. Отложим число на абаке. [Прибавим 2 единицы. Получим 4 десятка и 7 единиц, или число 47». 4 57-12 5+12 1 12=10+ 2 57-10=47 47- 2=45 2=10+ 2 45+10=55 55+ 2=57 или 45+12=45+10+2 57-12=57-10-2 Такой прием целесообразен потому, что при вычитании с переходом через разряд применение приема разложения на разрядные слагаемые двух компонентов приведет к вычитанию из меньшего числа единиц уменьшаемого большего числа единиц вычитаемого (43-17, 43=40+3, 17=10+7, 40-10, 3-7). 3 56-30=26 0+26=56 26+30=56 Полезно выполнять действия на счетах. Следует отметить, что некоторые учащиеся долгое время не могут научиться проводить рассуждения при решении примеров, но с их решением на счетах легко справляются, не смешивают разряды. Этим ученикам можно разрешать пользоваться счетами. Для большей наглядности, лучшего понимания позиционного значения цифр в числе запись единиц и десятков на доске и в тетрадях некоторое время можно делать разными цветами. Это важ*ю для тех учащихся, которые плохо различают разряды.
156 5 4) 45+ 5 45+25 45+5 0- 5 70-25, 50+45 50-5 _ 70-25 45+25
Рассуждения при решении этих примеров на сложение ничем не отличаются от рассуждений при решении примеров на сложение двух предыдущих видов, хотя последние и более трудны для учащихся. При рассмотрении случаев вида 50—5 надо указать на то, что необходимо занять один десяток, так как в числе 50 число единиц равно 0, раздробить десяток в единицы, от десяти отнять 5, а оставшиеся десятки сложить с разностью. 157 ч Для удобства и большей четкости изложения вычислительна приемов мы рассмотрели каждый новый случай изолированно. 1 процессе обучения учащихся устным вычислительным прием! необходимо каждый новый случай сложения или вычитания ря сматривать в неразрывной связи с предыдущими, постетч включая новые знания в уже имеющиеся, постоянно их сопост ляя. Например, 45+2, 45+5, 45+32, 45+35. Сопоставить примеры, найти общее и различное. Составить примеры такого вида. Такого рода задания позволят увидеть сходство и различие примерах, заставят учащихся думать, рассматривать каждый он чай сложения не изолированно, а в связи и взаимообусловленном ти. Это позволит выработать обобщенный способ устных вычислс ний. (Решить, сравнить вычисления и составить похожие приме ры: 40-6, 40-26, 40-36, 40-30.) 4 .10 42 7 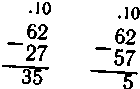 ) Сложение и вычитание с переходом через разряд (2-я труп па примеров) выполняются приемами письменных вычислений т. е. вычисления начинаются с единиц низших разрядов (с еди ниц), за исключением деления, а запись дается в столбик. ) Сложение и вычитание с переходом через разряд (2-я труп па примеров) выполняются приемами письменных вычислений т. е. вычисления начинаются с единиц низших разрядов (с еди ниц), за исключением деления, а запись дается в столбик. 100 100 5 6Т 35 Учащиеся знакомятся с записью и алгоритмами письменного сложения и вычитания и учатся комментировать свою деятельность. Необходимо сопоставлять различные случаи сначала сложения, затем вычитания, устанавливать черты сходства и различия, включать учащихся в процесс составления аналогичных примеров, учить их рассуждать. Только подобные приемы могут дать коррек-ционный эффект. Когда учащиеся научатся выполнять действия сложения и вычитания с переходом через разряд в столбик, их знакомят с выполнением этих действий приемами устных вычислений. т Например: 38+ 3 41-3 3+38 41-9 38+ 9 т 41-23 41-33 Объяснение обычно проводится на абаке, палочках, брусках или кубиках арифметического ящика, счетах. 158 штель предлагает прочитать пример, отложить на абаке 38, предварительно выяснив его десятичный состав. Снача-I единицам нужно прибавить 3 единицы: число 8 добавляется :ятка, т. е. прибавляются 2 единицы; образовавшиеся десять иииц заменяются одним десятком, получается 4 десятка. К 4 Гнткам прибавляется еще 1 единица. При вычитании из двузначного числа однозначного с перехо-через разряд сначала вычитаются все единицы уменьшаемого, I затем из круглых десятков вычитаются оставшиеся единицы Считаемого. П запись. 41-3=38 41-1=40 40-2=38 одробная 38+3=41 38+2=40 40+1=41 Как при сложении, так и при вычитании надо разложить второе лагаемое или уменьшаемое на два числа. При сложении второе лагаемое раскладывается на такие два числа, чтобы первое допол-яло число единиц двузначного числа до круглого десятка. При вычитании вычитаемое раскладывается на такие два Числа, чтобы одно было равно числу единиц уменьшаемого, т. е., I чтобы при вычитании получилось круглое число. При выполнении действий трудность для учащихся представляет умение правильно разложить число, выполнить последовательность нужных операций, запомнить и прибавить или вычесть оставшиеся единицы. Например, выполняя действие 54+8, ученик может правильно дополнить 54 до 60. Затруднение вызывает разложение числа 8 на 6 и 2. Число 6 ученик использует, чтобы получить круглое число, но сколько еще единиц осталось прибавить к круглым десяткам (к 60), он забывает. Учитывая это, необходимо, прежде чем рассматривать случаи данного вида, еще и еще раз повторить состав чисел первого десятка, провести упражнения на дополнение чисел до круглых десятков, например: «Сколько единиц не хватает до 50 в числах 42, 45, 48, 43, 4? Какое число нужно прибавить к числу 78, чтобы получить 80?» Надо рассматривать случаи вида 37+3+2=40+2=42 и добиваться ответа на вопрос: «Сколько всего единиц прибавили к числу (37)?» 43-3-2=40-2=38 159 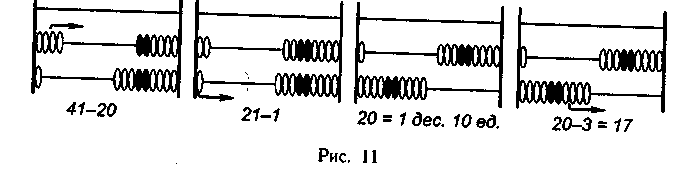 «Сколько всего единиц вычли из числа 43?» Значит, 43—5=я Для некоторых учащихся школы VIII вида при решении тал вида примеров используется частичная наглядность, наприм 38+7. Ученик откладывает на счетах 7 косточек или рисует палочек и рассуждает так: «К 38 прибавлю 2, получится 40 (и палочек 2 палочки убирает или зачеркивает), теперь к 40 приб лю еще 5 палочек». Еще пример: 45—8. Ученик откладывает 8 палочек и рассужу ет так: «Сначала от 45 отнимем 5, будет 40 (убирает 5 палоче^ осталось отнять 3. От сорока отнять 3, останется 37. 45—8=3? 38+24 54-18 Решение примеров данного вида базируется на уже извести учащимся приемах решения: 54-18 3 18=10+ 8 54-10=44 44- 8=36 8+24 24=20+ 4 38+20=58 58+ 4=62 Решение этих примеров основывается на разложении второ! слагаемого и вычитаемого на разрядные слагаемые и последовател| ном сложении и вычитании их из первого компонента действия. Школьники с нарушением интеллекта из-за неустойчивое! внимания, неумения сосредоточиться нередко допускают ошибк такого характера: прибавят или вычтут десятки, но забудут прибг вить или вычесть единицы. I Твердо не усвоив приема вычислений, позиционного значени| цифр в числе, ученики складывают десятки с единицами, вычитг ют из единиц уменьшаемого десятки вычитаемого: 54—18=43. I Сложение и вычитание с переходом через разряд учащиес^ должны уметь выполнять на счетах. Н |
