|
|
Методика преподования математики. Предисловие рецензенты доктор педагогических наук, профессор Н. М. Назарова кандидат педагогических наук В. В. Эк Перова М. Н
1ТЗНИЯ.
Важно постоянно подчеркивать, что складываются и вычитают-при решении таких примеров единицы. При записи примера 1ащиеся могут подчеркивать единицы: 14+2 = 16, 16—2 = 14. [ногда целесообразно единицы и десятки записывать разным цве-1М. На доске их можно обводить кружочком.
При решении примеров на сложение закрепляется умение учащихся пользоваться переместительным законом сложения: решение примера 2 + 14 проводится на основе решения примера 14+2. Полезно сопоставлять примеры на сложение и вычитание в пределах 20 с примерами на те же действия в пределах 10:
7+ 2= 9 9-2= 7 5+ 3= 8- 3=
2+ 7= 9 9-7= 2 3+...= 8-...=
17+ 2=19 19-2 = 17 17+ 2= 19- 2=
2+17=19 19-7=12 2+...= 19-...=
б) получение суммы 20 и вычитание однозначного числа из 20: 15+5 17+3 20-5 20-3
Решение примеров такого вида, особенно на вычитание, вызывает значительные трудности у многих умственно отсталых школьников. Учащихся смущает то, что при сложении единиц в разряде единиц получается нуль. Разложив 20 на два десятка и вычтя из одного десятка заданное количество единиц, дети забывают этот результат прибавить к десятку и получают ошибочный ответ: 20-3 = 7.
Использование наглядных пособий, актуализация имеющихся знаний и опора на них помогают преодолеть эти трудности. Необ-
139
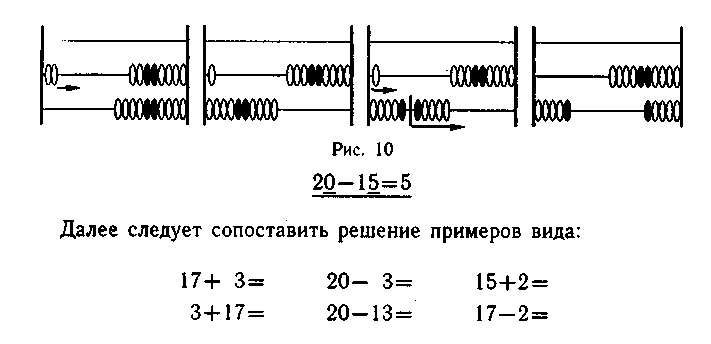
> ч
ходимо повторить таблицу сложения и вычитания в пределах 10. дополнение однозначного числа до десятка, вычитание из 10.
Объяснение сложения не представляет ничего нового по сравне нию с объяснением решения примеров вида 13+2, кроме образова ния 1 десятка: 5+5=10 (или 1 дес.); 1 дес. + 1 дес.=2 дес.=20. ^"Рассмотрим пример на вычитание: 20—3. В числе 20 нуль единиц, а нужно вычесть 3 единицы. Занимаем 1 десяток, раздроб ляем его на 10 единиц и вычитаем 3 единицы, получаем 7 единиц. Всего остается 1 десяток и 7 единиц, или 17. Проведенное рассуж-
Ш дение записывается так: 20—3=17.
В случае затруднений при понимании и приема вычислений объяснение можно провести с помощью палочек, связанных н пучки. Например, 20 — это 2 десятка (берем 2 пучка палочек) и нуль единиц. Занимаем 1 десяток и раздробляем его на 10 единиц (развязываем пучок палочек). 10 единиц минус 3 единицы получается 7 единиц. Всего остается 1 десяток и 7 единиц, или 17.
Решаются примеры на перестановку слагаемых, составляются по образцу, по аналогии:
2
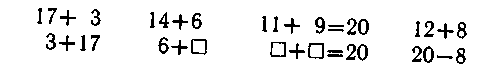

0-7 13+7
Действия сложения и вычитания сопоставляются: 15+5=20; 20-5=15;
/"в) вычитание из двузначного числа двузначного: 15—12; 20—15. х Решение примеров такого вида можно объяснить разными приемами:
разложить уменьшаемое и вычитаемое на десятки и единицы
и вычитать десятки из десятков, единицы из единиц;
разложить вычитаемое на десяток и единицы. Вычитать из
уменьшаемого десятки, а из полученного числа — единицы.'™^
Учащимся трудно знакомиться сразу с двумя приемами и даже трудно последовательно знакомиться сначала с одним, а потом с другим приемом. Умственно отсталые школьники самостоятельно не могут выбрать, когда целесообразнее использовать тот или иной прием. Поэтому знакомство с двумя, приемами только запутывает их. Лучше отработать хорошо один прием вычислений и научить учащихся самостоятельно пользоваться им.
„Объяснение вычитания проводится на наглядных пособиях. / Например, 15—12. «Какое действие надо выполнить? Прочитайте пример. Назовите уменьшаемое, вычитаемое. Сколько знаков имеют эти числа? Как они называются? Сегодня будем учить-140
пычитать из двузначного числа двузначное. Из чего состоит
ло 15? Отложим его на счетах. Из чего состоит вычитаемое Вычитать будем так: от 15 отнимем 1 десяток. Какое число
!лось? От 5 единиц отнимем 2 единицы. Какое число получи-
I, в остатке? Значит, 15—12=3».
Хналогично объясняется вычитание двузначного числа из 20 (рис. 10). Покажем на счетах последовательность вычитания дву-Н1.1чного числа из 20:
Целесообразно также использовать прием составления одного примера на сложение с тремя примерами: одного на сложение (перестановка слагаемых) и двух на вычитание. Необходимо сопоставлять компоненты этих примеров, подчеркивать их взаимосвязь (12+5, 5+12, 17-5, 17-12).
<'«Ттт „
\111. Сложение и вычитание с переходом через разряд представляет наибольшие трудности для учащихся школы VIII вида. Трудности связаны с тем, что сразу происходит актуализация ранее полученных знаний, их упорядочение и последовательное выполнение ряда логических операций. Чтобы сложить числа 7 и 5, нужно выполнить следующие операции:
Разложить второе слагаемое (5) на два числа так, чтобы
одно из них дополняло первое слагаемое до 10.
Дополнить первое слагаемое до 10, т. е. прибавить к перво
му слагаемому (7) одно из чисел, на которое разложили второе
слагаемое (т.е. 3). .
3. К полученному числу (10) прибавить оставшееся число (2)у
Учащиеся затрудняются, во-первых, в разложении второго сла
гаемого, так как, чтобы его разложить, нужно произвести мыслен-
141
• 1
но две операции: а) определить, сколько единиц недостает в н<-\ вом слагаемом до десятка; б) разложить второе слагаемое.
Вторая трудность заключается в том, чтобы удержать в пал число, которое осталось после дополнения первого слагаемой десятка, например: 7+5. Учащиеся дополнили 7 до 10, но помнят, сколько же нужно прибавить к 10.
Вычитание с переходом через десяток (12—5) тоже треб ряда операций:
Уменьшаемое разложить на десяток и единицы.
Вычитаемое разложить на два числа, одно из которых рапш
числу единиц уменьшаемого.
Вычесть единицы.
4. Вычесть из десятка оставшееся число единиц. ^
Учащихся вспомогательной школы в основном затрудняет вы
полнение третьей и четвертой операций.
Требуется большая подготовительная работа, тщательный под
бор материала от легкого к трудному, использование наглядности.
достаточное количество упражнений, которые бы помогли учл
щимся овладеть навыками решения примеров данного вида. Подготовительная работа должна заключаться в повторении
а) таблицы сложения и вычитания в пределе 10; б) состава чисел первого десятка (всех возможных вариантов из двух чисел), на пример: 7=6+1, 7=1+6, 7=5+2, 7=2+5, 7=4+3, 7=3+4; в) дополнения чисел до десяти: 10=3+..., 10=5+..., 10=8+..., 10=3 + ..., 10=... + ... и т. д.; г) разложения двузначного числа на десятки и единицы; д) вычитания из десяти однозначных чисел; е) рассмотрения случаев вида 17—7, 15—5.
9+1 = 10 12-2=10
= 11 10-1= 9
-1 = 11 12-2-1=9
Эта подготовительная работа должна проводиться систематически из урока в урок, задолго до решения примеров данного вида.
Последовательность случаев может быть различной. Существует два варианта:
1. Первое слагаемое и уменьшаемое постоянны, а второе слагаемое и уменьшаемое увеличиваются на 1:
9+2 8+3 7+4 11-2 12-3 9+3 8+4 7+5 11-3 12-4 9+4 8+5 ... 11-4
7+9 9+9 8+9
142
'2. Первое слагаемое и уменьшаемое меняются, увеличиваясь I, а второе слагаемое и вычитаемое постоянные: "•%.
8+3 7+4 6+5 7+6 11-3 11-4
9+3 8+4 7+5 8+6 12-3 12-4
9+4 8+5 9+6 13-4
9+5 и т. д.
Объяснение выполнения сложения и вычитания проводится с ^пользованием пособий и подробной записью. При выборе посопи необходимо учитывать, что учащиеся должны видеть необхо-|шость добавления первого слагаемого до десятка при сложении разложении уменьшаемого на десятки и единицы при вычитали. Удобными пособиями являются бруски и кубики арифмети-^ского ящика, абак, счеты.
Сложим 8+3. Откладываем на пособии (абаке, полосах) пер-Ье слагаемое и добавляем его до десяти. Десять единиц заменяем Ьсятком. К десятку прибавляем оставшиеся единицы:
8+3=11
3=2+ 1
8+2=10
10+1 = 11
На этом этапе полезно решение примеров вида
8
8+2+5 8+7
+7 8+2+5
Полезно также, особенно для наиболее слабых учащихся, ре-[ шение примеров с частичным использованием пособий, например: ' 7+5. Ученик берет 5 предметов (второе слагаемое 5) и рассуждает так: к 7 прибавить 3, будет 10 (отнимает от 5 предметов 3), осталось прибавить 2:10+2=12. В этом случае ученик помогает себе с помощью пособий разложить второе слагаемое и удержать в памяти оставшуюся часть.
Как вычесть из 11 число 2? На абаке откладываем 11. Надо вычесть 2. Вычитаем 1, осталось вычесть еще 1. 1 десяток заменяем 10 единицами. Из 10 единиц вычитаем 1. Остается 9.
1
11-2= 11-1 = 10 10-1= 9
1-2 = 11 = 10+ 1 И- 1 = 10 10- 1= 9
143
По аналогии со*.сложением рассматриваются случаи вы1 ния:
14-4-2 14-6
Учитель ставит вопросы: «Сколько единиц вычли сначг Сколько потом? Сколько всего единиц вычли?»
В дальнейшем учащиеся самостоятельно должны пояснять г говариванием громкой речью всё умственные действия.
Так же как и при сложении, можно позволить учащимся вычи таемое изображать на пособиях и убирать определенное количест во предметов при последовательном вычитании. (Иногда можно наблюдать, как учащиеся сами рисуют палочки на бумаге, а по мере вычитания зачеркивают их.) Например, 12—6. Откладывается 6 кругов (вычитаемое), и ученик рассуждает: «Сначала из двенадцати вычтем 2, будет 10 (убирает 2 круга), осталось вычесть 4: 10—4=6».
Так же как и во всех предыдущих случаях, соответствующие случаи сложения и вычитания необходимо сопоставлять.
Полезно сопоставлять ответы специально подобранных примеров целого столбика: решить и ответить на вопросы, почему ответы в примерах первого столбика увеличиваются, а в примерах второго уменьшаются.
9
9-3 9-4 9-5
+3 9+4 9+5
В упражнения необходимо включать примеры с тремя компонентами: 8+7+3, 17—4—8, 5+9—6, а также примеры, одним из компонентов которых является нуль, например: 19—9, 20—0, 15—15 (нуль в ответе). Хорошо сравнить решение примеров, компонентами или результатами которых являются нуль и единица: 15-1, 15-15, 15-0, 15-14.
Примеры на сложение следует чередовать с примерами на вычитание. При решении сложных примеров необходимо выработать привычку анализировать предлагаемый пример. Учить школьников планировать мыслительные действия, развивать ориентировочную основу познавательной деятельности. Этому способствуют вопросы такого характера: «Сколько действий надо выполнить? Какие это действия?»
Следует шире использовать составление примеров по данному: 144
7
15-8 15-7
+8=15 8+7
_ Так же как и при изучении действий в пределах 10, надо (предъявлять и такие примеры: 3—13, 12—15 — с целью выяс-'нить, возможно ли вычитание. При предъявлении пар примеров 5+15 и 5—15 (0+15 и 0—15) следует требовать объяснений, почему первый пример решить можно, а второй — нельзя. Подобные задания постепенно вырабатывают у учащихся привычку анализировать числа, прежде чем приступать к выполнению действий.
Для запоминания таблиц сложения и вычитания полезно решение примеров с неизвестным компонентом, составление нескольких примеров с данным ответом.
Таблицы сложения и вычитания заучиваются наизусть.
Вопросы и задания
1. Раскройте особенности изучения нумерации чисел второго десятка
в школе VIII вида (последовательность, методика, средства наглядности).
Сравните последовательность и методику изучения нумерации чисел
первого и второго десятка.
Составьте не менее 10 последовательно усложняющихся упражнений
для закрепления устной и письменной нумерации в пределах 20. На развитие
и коррекцию каких мыслительных процессов они направлены?
Составьте схему этапов изучения действий сложения и вычитания с
числами до 20.
Составьте фрагменты уроков, целью которых является ознакомление с
новыми вычислительными приемами сложения и вычитания чисел второго
десятка.
Познакомьтесь с планом изучения нумерации чисел второго десятка.
Дайте анализ этого плана. Сравните последовательность изложения этой
темы в учебнике математики для 2-го класса.
Глава 10
МЕТОДИКА ИЗУЧЕНИЯ НУМЕРАЦИИ СЛОЖЕНИЯ И ВЫЧИТАНИЯ В ПРЕДЕЛАХ 100
НУМЕРАЦИЯ В ПРЕДЕЛАХ 100
При изучении нумерации в пределах 100 школьники с нарушением интеллекта должны получить следующие знания и умения:
1. Научиться считать до 100 в прямом и обратном порядке единицами и десятками.
145
Уметь присчитывать и отсчитывать по 1, по 10 и равными
числовыми группами (по 2, 5, 20) как отвлеченно, так и н,1
предметных пособиях.
Уметь пользоваться порядковыми числительными.
Знать место каждого числа в натуральном ряду чисел и
пределах 100, понимать свойства этого ряда: каждое число н;\
единицу больше предшествующего и на единицу меньше после
дующего.
Понимать десятичный состав чисел. Уметь разложить число
на разрядные слагаемые и составить число из разрядных слагав
мых, знать разряды (единицы, десятки, сотни).
Уметь сравнивать числа, т. е. определять, какое число боль
ше или меньше другого, равно ему.
Уметь записывать и читать числа первой сотни, понимать
поместное значение цифр в числе.
Изучение нумерации в пределах 100 для умственно отсталых школьников связано с преодолением ряда трудностей. В период изучения чисел в пределах 100 закладывается основа понимания сущности десятичной системы счисления: из 10 простых счетных единиц образуется новая (составная) счетная единица — десяток, из 10 десятков образуется новая счетная единица — сотня. Вот эту закономерность умственно отсталые учащиеся усваивают с большим трудом. Здесь требуется основательная наглядная база, постоянное сравнение чисел первого, второго десятков и чисел 21—99, например: 2 и 20, 2 и 12, 1, 10, 100 и т. д. Учащиеся испытывают затруднения в запоминании названий круглых десятков, их последовательности и особенно их счета в прямом и обратном порядке. С большим трудом они запоминают названия десятков «сорок» и «девяносто». Нередко по аналогии с образованием предыдущих числительных они соответственно называют их: «четыредцать», «девятдесят», а при переходе к новому десятку считают: «Двадцать девять, двадцать десять, двадцать одиннадцать» и т. д. Как и при изучении предыдущих чисел, учащихся больше всего затрудняет счет в обратном порядке, присчитывание и отсчитывание равными числовыми группами.
При изучении письменной нумерации многие учащиеся долго не усваивают позиционное значение цифр в числе: вместо 35 записывают 53, при чтении чисел вначале произносят единицы, а потом десятки. Некоторые учащиеся, усвоив образование новых десятков, еще долгое время испытывают затруднения в понимании образования числа 100. Овладев устной нумерацией, некоторые учащиеся не могут овладеть письменной нумерацией (устно счита-146
«>т верно, а записывают числа от 1 до 100 по порядку неверно). Некоторые учащиеся, наоборот, правильно записывают числовой 1>нд, а при устном пересчете допускают ошибки.
Причины этих трудностей заключаются и в трудностях самого математического материала, и в психических особенностях учащихся, и в имеющих еще место недостатках организации изучения данного материала: некоторая поспешность в отказе от использования наглядных пособий, недостаточное их разнообразие, ограничение изучения темы небольшим периодом времени и недостаточное количество упражнений на закрепление этого материала при изучении последующих тем.
Какие требования предъявляются к изучению данной темы?
Хорошее знание нумерации первого и второго десятка.
Использование разнообразных наглядных пособий и дидакти
ческого материала не только при знакомстве учащихся с новыми
понятиями, но и в процессе закрепления и повторения знаний по
нумерации, включение каждого ученика в активную практическую
деятельность с дидактическим материалом.
Систематическое повторение нумерации при изучении после
дующих тем математики, разнообразие заданий и упражнений для
самостоятельной работы, включение вариативных упражнений в
устный счет, активизация творческой и речевой деятельности уча
щихся.
При изучении данной темы могут быть использованы наглядные пособия и дидактический материал: 100 палочек, связанных в пучки по 10 штук, арифметический ящик, абаки (классный и индивидуальные), счеты (классные и индивидуальные), метровая линейка, 10 полос, разделенных на 10 равных квадратов, монетная касса — 10 гривенников, 1 рубль, квадраты (10x10) с числами от 1 до 100, с четными числами, с нечетными числами; таблица разрядов (с разрядами единиц, десятков, сотен), цифровая касса и таблички с круглыми числами (10, 20, 30, 40, ..., 100).
Последовательность изучения нумерации в пределах 100: повторение нумерации в пределах 10 и 20; изучение нумерации круглых десятков; изучение нумерации чисел от 21 до 99 (сначала устной, затем письменной).
Изучение нумерации круглых десятков
Урок, на котором учитель будет знакомить учащихся с нумерацией круглых десятков, необходимо начать с повторения образования десятка из простых единиц. С этой целью предлагается отсчи-
147
тать 10 палочек и связать их в пучок. 10 палочек, связанных|
1 пучок, — это десяток палочек. Счет продолжается до 20. 10 г
лочек снова связываются в пучок. 1 десяток, или десять палоче
2 десятка, или двадцать палочек. Считаем, присчитывая по однол
десятку палочек. Один десяток, два десятка, три десятка, ш
тридцать, четыре десятка, или сорок, ..., 9 десятков, или девяно
то, прибавляем еще 1 десяток, получаем 10 десятков, или ст(
Один десяток (десять) — это 10 единиц. Два десятка (два;
цать) — это двадцать единиц и т. д. Подобные упражнения пров<
дятся и на других пособиях (арифметический ящик, счеты, мон<
ты и т. п.).
Учитель каждый раз обращает внимание на то, что счет десятка ми ведется так же, как счет единицами. Обращается внимание уча щихся и на обозначение чисел числительными. Первое слово в на! звании числа показывает число десятков: двадцать, тридцать, ...I пятьдесят и т. д. Полезно показать таблицу и читать числительны^ парами: два — двадцать, три — тридцать и т. д. В первом ряду счет ведется простыми единицами, а во втором — десятками:
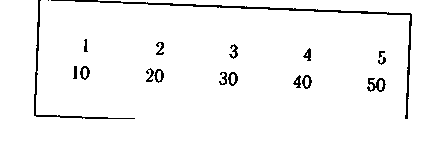
I
Письменная нумерация круглых десятков может быть дана по аналогии с записью уже известных учащимся чисел 10 и 20. В числе 10 один десяток, цифра 1 записывается на втором месте справа, а на месте единиц записывается нуль. В числе 20 два десятка и нет отдельных единиц (показать на абаке, на счетах), цифра 2 записывается на втором месте, а на месте единиц записан 0. В числе 30 три десятка, число десятков 3, а на месте единиц 0 и т. д.
Полезно использовать таблицу также для сравнения чисел первого десятка и круглых десятков. Учащиеся должны учиться сравнивать рядом стоящие числа по рядам и столбцам: 2>1 на 1 ед., 2 дес.>1 дес. на 1 дес., 20>10 на 10 ед.
Учащиеся реально не представляют себе множества чисел, находящихся между круглыми десятками. Поэтому на следующем уроке, закрепляя счет круглыми десятками, необходимо познакомить учащихся с образованием чисел 21—99.
148 |
|
|
 Скачать 4.24 Mb.
Скачать 4.24 Mb.