Методика преподования математики. Предисловие рецензенты доктор педагогических наук, профессор Н. М. Назарова кандидат педагогических наук В. В. Эк Перова М. Н

• Название: Предисловие рецензенты доктор педагогических наук, профессор Н. М. Назарова кандидат педагогических наук В. В. Эк Перова М. Н
• Анкор: Методика преподования математики.doc
• Дата: 09.02.2018
• Размер: 4.24 Mb.
• Имя файла: Методика преподования математики.doc
• Тип: Документы; #15378
• страница: 12 из 37

\*_л Получение чисел

Покажем, например, получение числа 4. Учитель предл; сосчитать листья. «Сколько здесь желтых листьев?» — спраи ет учитель, указывая на 3 листочка. Ученики пересчитываь отвечают: «Здесь 3 листочка». «С дерева упал еще 1 крас лист. Посчитаем, сколько всего листьев стало. Как получило листочка? Сколько желтых листочков лежало? Сколько у! красных листочков? Сколько же стало листочков?» Затем расе ривается получение числа 4 на других пособиях (счетных поде ках, счетах и т. д.). «Так как же получить число 4? К как числу нужно прибавить единицу?» — этими вопросами учит подводит учащихся на основе рассмотрения конкретных случ получения числа 4 к обобщению: «Число 4 получится, если к трем прибавить один». Такой вывод могут сделать самостоятельно ш¹ все ученики 1-го класса, но некоторым он уже доступен. Затем учитель показывает, что если из четырех листочков «улетит» один листочек, то останется 3 листочка. Учащиеся убедились в новом способе получения числа 3.

При изучении числа 5 учитель знакомит учащихся и с получе­нием числа 4 вторым способом: вычитанием из числа 5 одной . единицы.

К концу 1-го класса учащиеся должны понимать, что каждое число первого десятка образуется из предшествующего путем при­бавления одной единицы, а если из числа вычесть единицу, то получится предшествующее число.

Получение числа закрепляется различными упражнениями. Примерные виды заданий: «Отложите на счетах 3 красные косточ­ки. Прибавьте столько желтых косточек, чтобы получилось 4. Наклейте или раскрасьте 3 синих круга и 1 красный. Сколько всего кругов получилось? Обведите 3 клеточки синим каранда­шом. Сколько клеточек надо еще обвести, чтобы их стало 4? Положите 3 копейки. Сколько денег надо прибавить, чтобы полу­чилось 4 копейки?»

Учитель раздает каждому по 3 шарика: «Сосчитайте шарики и вылепите еще столько шариков, чтобы их стало 4». Учащимся, которые сами не справляются с таким заданием, учитель оказыва­ет помощь.

Далее учащиеся учатся считать элементы предметных совокуп­ностей из 4 элементов.

112
Учащиеся школы I! вида должны по-мть, что числа по­лются не только в 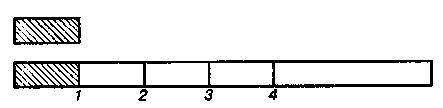/льтате счета, но

результате изме- Рис. 5

ия. Поэтому при получении чисел полезны и упражнения на адывание мерки в полоске или отрезке и подсчет числа мерок чала в полоске (рис. 5), а затем в мерной (масштабной) линей-Линейка с нанесенной на ней сантиметровой шкалой является |м1[юшим наглядным пособием при рассмотрении вопросов нумера-III (в частности, получения чисел).

Обозначение числа цифрой и письмо цифр

После знакомства с получением числа учитель учит обозначать ^гзто число цифрой, как печатной, так и рукописной. Цифра внима­тельно рассматривается, выделяются ее элементы, подыскиваются предметы, с которыми можно сравнить цифру. Это нужно для того, чтобы учащиеся лучше запомнили образ цифры, не смешива­ли его с другими цифрами (например, цифра 8 — это две баран­ки; цифра 1 — палочка и крючок). "'"

Учитель ставит цифру под соответствующим количеством пред­метов или под картинкой с изображением предметов, соответству­ющих по количеству данной цифре.

Далее надо обучить ребят письму цифр. Это довольно сложный процесс. В пропедевтический период учитель должен хорошо вы­яснить возможности и особенности написания цифр каждым уче­ником класса! Для учащихся, у которых процесс письма по тем или иным причинам затруднен, необходимо заранее приготовить дополнительные пособия (фанерные или пластмассовые цифры для обводки, лекала с прорезями — в них можно вставить каран­даш и писать цифры, обводя прорези).

Последовательность знакомства с написанием цифр:

1. 
   показ рукописного образца цифры, показ и письмо элемен­
   тов цифры;
   
2. 
   показ учителем письма цифры на доске (при этом обращает­
   ся внимание на направление движения мела);
   
3. 
   обводка (пальцем, указкой) модели цифры;
   
4. 
   письмо цифры в воздухе;
   
5. 
   письмо цифры на доске несколькими учениками;
   

ИЗ

6) письмо цифр в тетрадях по образцу. ^Предварительно учи тель готовит тетрадь, в которой ученикам предстоит писат цифры. Для всех учащихся дается образец: записываются 2— > цифры.

Для отдельных учащихся учитель пунктиром или тонкими ли­ниями пишет цифры, а они лишь обводят их. Некоторым ученикам необходимо поставить лишь две-три опорные точки. у Если у ученика значительные нарушения моторики, мелкиг \ движения пальцев рук затруднены, то они не смогут писать цифры в одну клеточку. Таким учащимся разрешается писать цифры в две клеточки, а то и крупнее (в клетках, специально разграфленных для этого учителем).

Учащимся, которые не ориентируются на странице тетради, не соблюдают строчек при написании цифр, необходимо выделять (проводить) строчки синим карандашом.

О
\
тдельным учащимся доступна лишь обводка цифр по лекалу или трафаретам, письмо вместе с учителем.

Перед письмом цифр учащимся предлагается обвести цифры из наждачной бумаги или фланели, наклеенные на карточках. Ребе­нок водит пальцем по цифре, как бы вычерчивая ее, затем повто­ряет ее название. Письмо цифр сочетается с их проговариванием, а также счетом (написать одну, две, три, четыре цифры).

Учитель добивается от каждого ученика правильного, четкого написания цифр, что является залогом правильных вычислений при решении примеров и задач.

Соотношение количества, числа и цифры

Учащиеся школы VIII вида вначале не связывают число с циф­рой. Осознание такого соотношения требует многочисленных уп­ражнений разнообразного характера, например:

1. К заданному количеству предметов подобрать нужную цифру. Учитель говорит: «Мама купила 4 апельсина. Покажите цифрой, сколько апельсинов купила мама. Проверим. Посчитаем вместе, хором, и прикрепим цифру 4».

2. К цифре подобрать соответствующее количество предметов.
«Эта кукла не умеет говорить, но знает цифры. Смотрите, какую
цифру она показала (3). Это она просит конфеты. Сколько конфет
она просит? Дадим кукле 3 конфеты».

3. Игра «Найди нужные картинки». Ученики получают коробоч­
ки с набором картинок (5—6 картинок) и цифру. К цифре они
114
лжны подобрать все картинки с соответствующим количеством сдметов.

Затем к каждой картинке ученик подбирает нужную цифру.

4. На полоске отложить мерку 4 раза. Какое число получи-• •сь? Измерить воду в банке стаканами. Отсыпать из пачки 4 ножки соли, написать цифрой. Сколько соли отсыпали? И т. д.

Место числа в числовом ряду

Работу следует начать с числовой лестницы.'Одну ступеньку <^означаем числом 1, две ступеньки — числом 2, три ступень­ки — числом 3, четыре ступеньки — числом 4. Дети «поднимают-ся» и «опускаются» по «лесенке» (ведут счет).

Затем определяется место числа в числовом ряду. Например, цифра 4 стоит после цифры 3, так как число 4 идет после числа Л при счете. Учащиеся в своем наборном полотне находят цифру 4 и расставляют все известные им цифры по порядку, т. е. в порядке последовательности числового ряда. Учащиеся должны знать, что число 4 стоит после числа 3 и перед числом 5. «Сосе­ди» числа 3 — числа 2 и 4. Между числами 3 и 5 стоит число 4. На этом этапе полезна работа с иллюстрацией чисел соответству­ющим количеством предметов. ;

Наряду с составлением числового ряда с опорой на предметное и иллюстративное его изображение все чаще следует воспроизво­дить ряд без опоры на наглядно-образное восприятие: записать числа по порядку от 1 до 4; записать числа от 4 до 1; заполнить числовой ряд 1, 3; вставить пропущенные числа (или закрыть «форточкой»); найти соседей числа П 2 П.

Учитель коррекционной школы для закрепления последователь­ности числового ряда широко использует разнообразные игры, как дидактические, так и подвижные, занимательные упражнения. Особенно любят дети игры «Живые цифры», «Найди свое место», «Угадай, сколько здесь грибочков» и др.

Счет в прямой и обратной последовательности

Обучение счету в пределах данного числа происходит после знакомства учащихся с его образованием. Если учащиеся пришли в 1-й класс школы VIII вида, умея считать в пределах 10, то этот счет необходимо закреплять и совершенствовать.

115

г

Прежде всего учитель учит брать предмет в руку и отклады вать его в сторону, затем отодвигать. Потом ученики считают, дотрагиваясь пальцем до каждого предмета, затем только показы вают предметы, не дотрагиваясь до них. После этого они считаю; «глазками», т. е. смотрят на предметы. Во всех этих упражнениях ученики считают вслух. И только тогда учитель просит пересчи тать предметы про себя.

Каждый раз после пересчета предметов учитель задает вопрос: \ «Сколько?» Например: «Сколько здесь карандашей, посчитай». v После пересчета учитель опять спрашивает: «Здесь 7 каранда­шей?» (Карандаши можно собрать в одну руку.)

Первые предметы, которые пересчитывают учащиеся, должны быть хорошо им известны, не надо отвлекать учащихся новизной, излишней красочностью. Все внимание должно быть сосредоточе­но на счете.

Для счета сначала выбирают одинаковые предметы. Затем берут однородные предметы, отличающиеся размером, цветом, ма­териалом. Учащиеся пересчитывают предметы, объединяя в одну совокупность множество синих и красных карандашей, больших и маленьких шаров, деревянных и пластмассовых палочек различ­ной окраски.

Наконец, они пересчитывают и разнородные предметы: «Сколь­ко деревьев (берез и елей) стоит в ряду?», «Сколько игрушек?».

Счет ведется как слева направо, так и справа налево, сверху вниз, снизу вверх. При пересчитывании важно, чтобы ученик не только называл результат счета: «Здесь 5 игрушек», «Стоят 7 деревьев», но и правильно показывал все множество сосчитанных предметов.

Когда учащиеся научились пересчитывать предметы в горизон­тальном ряду, надо варьировать расположение предметов, предъяв­ляя их в вертикальном, наклонном рядах, в сложной группе (враз­брос). Это необходимо делать потому, что в силу стереотипности мышления первоклассники не могут использовать свой опыт счета горизонтально расположенных предметов при счете предметов, дан­ных в ином положении. Только разнообразные упражнения в счете разных предметов, различно расположенных в пространстве и на плоскости, помогают сформировать у учащихся навыки счета.

Отвечая на вопрос: «Сколько?», учащиеся учатся считать от­дельные предметы, предметы, объединенные в цепочки (ребенок может дотронуться, отодвинуть предмет при счете, но не может 116
|ять его в руки), изображения предметов на картинках, табли-«х, числовых фигурах (ребенок может дотронуться до предметов, ||(| не может отодвинуть их, взять в руки). Счет в двух последую­щих случаях более труден.

Сначала дети учатся присчитывать по одному предмету, а Потом отсчитывать, затем считать и равными числовыми группа­ми — по 2, 5, 3, 4.

Счет в обратном порядке более труден для учащихся, поэтому он должен быть связан с отсчитыванием сначала конкретных предметов, которые ученик мог бы взять в руки, отодвинуть. Например: «Сосчитаем карандаши». Ученик сосчитал: «Всего 5 карандашей». «Уберем 1 карандаш в коробку. Осталось 4 каранда­ша. Уберем еще 1 карандаш. Осталось 3 карандаша» и т. д. Затем отрабатывается обратный счет на цепочках, счетах и, наконец, отвлеченно.

В период обучения даются не только задания на пересчитыва­ние предметов, но и задания практического характера'^ например: «Леня, сосчитай, сколько учеников в нашем классе сидит у окна»; «Каждому ученику нужно дать по 1 тетради. Сколько тетрадей нужно отсчитать?»; «Отсчитай, Катя, 7 тетрадей»; «Алеша, дай мне 3 карандаша».

Усвоение счета, восприятие определенного количества и соот­ветствующего числа значительно облегчается, если в упражнения; включаются различные анализаторы: зрительный, слуховой, осяза­тельный. Можно пользоваться такими приемами: хлопать ладош­ками, звонить колокольчиком, постукивать о парту, ударять по клавишам пианино, прыгать, топать, ударять мячом об пол и т. д. При этом учитель постоянно указывает на число тех или иных движений, звуков, которые нужно произвести («Попрыгай на одной ноге 4 раза, похлопай ладошками 3 раза»), просит опреде­лить их количество («Сколько раз я ударила палочкой о стол? Сколько раз я дернула шнурок с шариком?»).

Нередко непривычность задания отвлекает ребенка своей новой формой, а быстрая отвлекаемость, неумение сосредоточить внимание на решении основной задачи приводит к тому, что ребе­нок забывает об основном задании: «Подпрыгни 3 раза». Ученик прыгает и забывает о счете. «Хлопни 5 раз», — говорит учитель. Ученик хлопает, пока его не остановят. Чтобы избежать этого, учитель должен сосредоточить внимание ученика на второй части

117


\ задания: «Сколько раз нужно хлопнуть? Прыгай и считай в| '""Когда ты остановишься?»

Многократная повторяемость подобных упражнений привод к тому, что форма задания не отвлекает учеников и внимание сосредоточивается на счете.

Учащиеся выполняют практические задания: обводку, лепку аппликацию, раскрашивание, связывая эту работу со счетом. Учи тель просит обвести три кружка, раскрасить два гриба, наклеит! три листочка дуба, вылепить четыре шарика.

Уроки математики должны быть тесно связаны с уроками руч ного труда, рисования: учащиеся лепят большие и маленькие ша­рики, пересчитывают их, лепят грибы, овощи, фрукты и они ста­новятся предметом счета на уроках математики.

Следует учить учащихся счету предметов и отвлеченному счету не только от единицы, но и от любого числа до заданного: «Посчи­тай от 3 и дальше»; «Посчитай от 4 до 8»; «Посчитай (обратно) от 10 до 5»; «Посчитай от 7 до 3»; «В корзине 5 яблок, клади туда еще яблоки и считай, сколько всего яблок будет в корзине»; «В корзине 5 яблок, отсчитай (возьми) 2 яблока. Сколько яблок останется в корзине?» (Отсчитывать надо так: «Там 5, возьму 1 яблоко, осталось 4, возьму еще 1, осталось 3».)

При изучении каждого из чисел учащиеся учатся не только пересчитывать предметы и отвечать на вопрос «Сколько?», но и определять порядковый номер того или иного предмета (в зависи­мости от порядка, в котором проводится счет).

Определение порядкового номера пересчитываемых предметов имеет большое значение для развития пространственных представле­ний, так как ученики знакомятся с порядковым отношением, местом предмета в ряду других: перед, между, за, около — это слова, которые указывают на пространственное положение предмета.

Начинать работу следует в подготовительный период. Лучше всего знакомство с этими понятиями проводить как бы исподволь, обращая внимание учащихся на отношения между предметами в окружающей среде: «Кто сидит рядом с тобой, Юра? Кто сидит перед (за) тобой, Наташа? К доске выйдут Саша и Миша. Соня, встань между ними. Ребята, кто стоит первым слева? Кто второй, третий? Кто стоит первым справа? Кто второй? Кто третий? Сей­час мы пойдем завтракать. Постройтесь в два ряда — девочки и мальчики. Пересчитайтесь по порядку сначала мальчики. Начина-118
счет слева». Мальчики считают: «Первый, второй...» Девочки ^ют: «Первая, вторая...»

I Трудности у учащихся вызывает изменение порядковых числи-Льных по родам, поэтому закрепляющих это упражнений долж-

быть достаточно много. Учащиеся должны понять, что первым »кет быть предмет, расположенный слева, справа, сверху, тзу, что один и тот же предмет в зависимости от направления

• чета может быть и первым, и последним.

Необходимо показать учащимся, что для ответа на вопрос

• Сколько?» им нужно определить общее число пересчитываемых
предметов, а при ответе на вопрос «Который?» — назвать номер
предмета по порядку. Например, учитель просит выйти к столу
нескольких учеников и построиться в ряд. «Посчитаем, сколько
учеников стоит у доски», — говорит учитель. Учащиеся хором
считают: «5 учеников». «Сколько всего учеников? Покажите 5
учеников. Кто стоит первым слева в ряду? Который по счету
Сережа? Пересчитайтесь по порядку номеров. Кто пятый в ряду?
Покажите пятого ученика». Учащиеся должны понять, что 5 —
это общее количество, а пятый — это один ученик, стоящий
пятым по порядку.

Очень важно учащихся 1-го класса учить изменению числи­тельных по родам при счете предметов. Эта задача трудна для умственно отсталых учащихся. Поэтому полезно подбирать для счета предметы, при пересчете которых необходимо употреблять числительные разного рода: карандаш — один, два, три...; тет-/' радь — одна, две, три...; яблоко — одно, два, три... Особое вни­мание следует уделять счету предметов, обозначаемых числитель­ными среднего рода, так как они чаще всего неправильно употреб­ляются учащимися.

Сравнение предметных совокупностей. Сравнение чисел

По мере изучения чисел первого десятка учитель не только знакомит учащихся с местом данного числа в натуральном ряду чисел, но и учит сравнивать это число с числами, стоящими рядом, а также другими числами. Например, уже при изучении числа 2 учитель показывает учащимся, что 2 больше 1. Вначале это сравнение проходит на предметных множествах: «В верхнем ряду 1 круг, а в нижнем — 2 круга. Где кругов больше? Где меньше? Почему? В каком ряду лишний круг? В каком ряду не

119

хватает кругов?» Аналогичные упражнения проводятся и на дру гих множествах: «Какую цифру поставим около одного круга! Какую цифру поставим около двух кругов? Какое число больше 2 или 1? Какое число меньше: 2 или 1? Почему 2 больше, чем 1? Покажи сначала на кругах, а потом на яблоках».

Далее учитель просит уравнять количество кругов в верхнем и

/ нижнем рядах: «Что нужно сделать, чтобы в верхнем ряду было

столько же кругов, сколько в нижнем?» (Добавить 1 круг.) «Что

нужно сделать, чтобы в нижнем ряду кругов было столько же,

сколько в верхнем?» (Убрать 1 лишний круг.)

Учащиеся работают в этот период в основном с множеством предметов, устанавливая взаимно однозначное соответствие между элементами множеств: они не только выясняют, где пред­метов больше (меньше), но и определяют, сколько лишних пред­метов в большем множестве и сколько их недостает в меньшем. Одновременно они сравнивают и числа, которые являются харак­теристикой этих множеств. Сначала сравниваются два рядом стоя­щих числа, например 3 и 4, а затем и любые два числа.

Например, сравниваются множества яблок и груш (яблок 3, а груш 4). Ученики раскладывают груши в ряд, а под каждой грушей кладут яблоко, т. е. устанавливают взаимно однозначное соответст­вие. Одна груша лишняя — груш больше. Одного яблока недоста­ет — яблок меньше. Значит, 4 больше, чем 3, а 3 меньше, чем 4. Полезны и такие вопросы:

«Сколько надо добавить яблок, чтобы их стало столько же, сколько груш?»

«Сколько надо отнять груш, чтобы их стало столько же, сколь­ко яблок?»

«Сосчитаем, сколько тетрадей в стопке (7 тетрадей). Сколько нужно для них обложек?»

«Нарисуйте 4 кружочка. Возьмите столько же треугольников. Сколько треугольников надо взять?»

Затем учащиеся сравнивают числа, абстрагируясь от конкрет­ных множеств: «Какое число больше: 5 или 6? Сколько лишних единиц в числе б? Сколько их недостает в числе 5? Что нужно сделать, чтобы уравнять числа?»

Учащиеся должны хорошо усвоить, что все числа, предшест­вующие данному (те, которые стоят в числовом ряду перед дан­ным числом, раньше его, ближе к началу числового ряда), меньше данного, а все последующие числа (те, которые стоят после дан­ного в числовом ряду, дальше от начала) больше данного. Исполь­зование иллюстративной таблицы с изображением множеств и 120
1, а также «числовой лестницы» поможет учащимся в сравне-1исел, известного им отрезка числового ряда.^ пя закрепления сравнения чисел могут быть использованы «нения: «Сосчитай, сколько здесь синих шаров. Покажи циф-«Отсчитай красных шаров больше. Покажи, сколько крас-шаров ты отсчитал», «Какое число больше (меньше)?», лько лишних единиц в большем числе?» (Аналогичное упраж-к-мие с использованием понятий «столько же», «меньше».) Подоб-,ыс упражнения можно проводить с хлопками, прыжками и т. д.: Покажи число три», «Покажи числа, большие числа 3», «Покажи Только же пальчиков. Покажи пальчиков больше (меньше)».

Число 10, которым заканчивается изучение первого десятка, тличается от ранее изученных чисел. Учащимся 1-го класса ||ожно дать только один способ образования этого числа: 9+1. 1исло 10 обозначается не одной, а двумя цифрами 1 и 0, и

[местно дать учащимся термины однозначные числа и двузнач-ые числа. Однозначные числа записываются одной цифрой. Дву-начное число 10 записано двумя цифрами. Какой-либо четкой лфференциации однозначных и двузначных чисел провести при

[том нельзя, так как учащиеся знают только одно двузначное исло. Однако эти термины ввести следует. Необходимо при этом ^закрепить понятия число и цифрси

Десять единиц дети учатся объединять в один десяток, пользу­ясь рассыпными палочками и связкой палочек, 10 косточками на первой проволоке счетов и 1 косточкой (одним десятком) на вто-, рой проволоке; работая с абаком, дети заменяют 10 кружков в первом столбце, обозначающем разряд единиц, одним кружком во 'втором столбце, 10 монет по одной копейке — одной монетой в 10 копеек, 10 квадратиков — полоской, на которой они укладыва­ются в ряд, и т. д. На многочисленных упражнениях с использо­ванием разнообразных наглядных пособий и дидактического мате­риала следует отдифференцировать понятия десять единиц и один десяток.

Обучение сложению и вычитанию в пределах 10

•**'* С арифметическими действиями учащиеся знакомятся сразу же

после изучения числа 2. Изучение каждого из чисел первого десятка (кроме 1) завершается изучением действий сложения и вычитания в пределах этого числа. Действия сложения и вычита­ния изучаются параллельно.

121

Учащиеся знакомятся со знаками сложения — плюсом (+) вычитания — минусом (—) и знаком равенства — равно ( = ).

При изучении данной темы учащиеся должны овладеть вычис лительными приемами, получить прочные вычислительные навы ки, заучить результаты сложения и вычитания в пределах 10, а также состав чисел первого десятка, узнавать и показывать ком поненты и результаты двух арифметических действий (сложения и вычитания) и понимать их названия в речи учителя.

В основе сложения и вычитания в пределах 10 лежат операции с предметными совокупностями и некоторые вычислительные приемы. Изучение состояния знаний учащихся, поступивших в 1-й класс вспомогательной школы, показывает, что большинство из них либо вообще не имеют представления о действиях сложения и вычитания и вычислительных приемах, либо находят результаты этих действий путем операций над предметами. Поэтому обучение учащихся арифметическим действиям сложения и вычитания не­обходимо начать с этапа овладения всеми учащимися операциями над предметными совокупностями. Предметно-практическая дея­тельность детей сопровождается счетом: «К одной лампочке при­бавить еще одну лампочку. Сколько получится лампочек?» Это записывается так: 1 + 1=2. Учащиеся на партах прибавляют к одному предмету еще один предмет и пересчитывают результат.

Запись примеров идет на доске и в тетрадях. Учащиеся учатся читать пример: «К одному прибавить один, получится два». На этом же уроке учащиеся знакомятся с решением и записью при­меров на вычитание. Пример читают так: «От двух отнять один, получится (останется) один». ,

^

После знакомства с числом 3 дети учатся решать примеры вида 2+1, 1+2, 3—1, 3—2. Чтобы решить пример 2+1, надо отсчитать 2 предмета (2 красных круга), а потом отсчитать еще 1 предмет (зеленый круг), соединить их, пересчитать и записать ответ. Учитель обращает внимание учащихся на то, что когда прибавляют, то становится больше, чем было.

При вычитании 3—2 ученик должен взять 3 предмета, отсчи­тать (удалить) 2, пересчитать оставшиеся предметы и записать ответ. Учитель обращает внимание на то, что когда вычитают, то становится меньше, чем было.

1 Одновременно на этом же этапе организуются наблюдения уча­щихся над свойством сложения. Учитель показывает, что если к двум красным кругам прибавить один зеленый, то получится три 122
а. И наоборот: если к одному зеленому кругу прибавить два ных, тоже получится три круга. )Учащиеся наблюдают пере-•ительное свойство сложения. Учитель обращает внимание на 'становку групп предметов, чисел в примерах и неизменность при этом результата. Учащиеся подводятся к доступным им обоб­щениям.

Но мере овладения учащимися натуральной последователь­ностью чисел и свойством этого ряда (каждое число меньше сле­дующего за ним на единицу и больше стоящего перед ним на единицу) нужно знакомить их и с приемом сложения и вычита­ния, опирающимся на это свойство натурального ряда чисел) Дети учатся этим приемом прибавлять и вычитать единицу из числа, т. е. присчитывать и отсчитывать по 1.

Пособием для овладения этим приемом должен быть натураль­ный ряд чисел от 1 до числа, которое учащиеся изучают. (Число­вой ряд постоянно должен находиться на наборном полотне в классе и на партах учащихся.) Например, надо решить: 3+1. Учитель показывает цифру 3 в числовом ряду и просит найти число на 1 больше. Это следующее в числовом ряду число 4, значит, 3+1=4. Пример 3—1 'решается так: находим число 3, число на единицу меньше — это число, которое стоит перед числом 3, т. е. число 2. Значит, 3—1=2._хДети успешно пользуют­ся табличкой числового ряда, котораяТГомогает овладеть вычисли­тельным приемом без опоры на конкретный материал.

Когда учащиеся научились прибавлять и вычитать по 1, надо учить их прибавлять по 2: к четырем прибавить 2. Ученик ставит палец на число 4 в числовом ряду, прибавляет 1, получилось 5, еще прибавляет 1, получилось 6. Палец ученика скользит по числовому ряду.

С первых уроков математики целесообразно обучать комменти­ровать свою деятельность с предметами и числами. Сначала учи­тель сам комментирует производимые им совместно с учениками действия, а учащиеся повторяют. Постепенно доля самостоятель­ности в комментировании деятельности у учащихся увеличивает­ся, а помощь со стороны учителя уменьшается.

Переходным этапом от операций над конкретными множества­ми к действиям над числами является знакомство учащихся (при выполнении сложения и вычитания) с приемом присчитывания и отсчитывания нескольких единиц.

123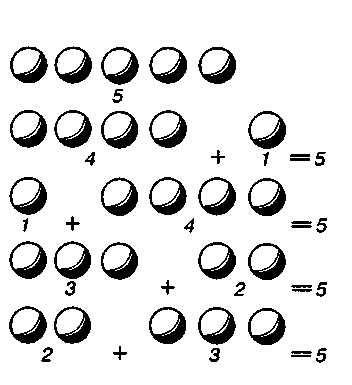



" ,3»* X

/ При использовании приема присчитывания учащиеся пересчи тывают первое множество, запоминают это число, к нему по одно му присчитывают элементы второго множества и .сразу говорят сумму. Например: 2+2=? Учитель говорит: «Сосчитаем яблоки и корзине. Их 2. Нужно прибавить к ним еще 2 яблока. Узнаем, сколько всего яблок в корзине. Считать будем так: к двум приба вим еще 1, будет 3 и еще 1, будет 4. В корзине 4 яблока, значит 2+2=4. Проверим, что в корзине 4 яблока (пересчитаем)». Затем учащиеся не пересчитывают первое множество, а сразу называют число. В коробке 3 карандаша. Прибавим еще 2 карандаша. Счи­таем так: к трем прибавим 1, будет 4, прибавим 1, будех_й

Когда учащиеся овладели приемом присчитывания, учитель знакомит их с приемом отсчитывания: 5—2=? На наборном по­лотне выставляются 5 кругов. Нужно отнять 2 круга. Отсчитыва­ем 1, осталось 4, отсчитываем еще 1, осталось 3, значит, 5—2=3.' Если приемом присчитывания ученики 1-го класса овладевают довольно быстро, то приемом отсчитывания — намного медлен­нее. Особенно это относится к ученикам со значительной сте­пенью умственной отсталости. Трудность состоит в том, что прием отсчитывания основан на хорошем знании обратного счета, а об­ратный счет для многих учащихся 1-го класса труден. Кроме того, ученики плохо запоминают, сколько нужно отнять, сколько уже отняли, сколько еще надо отнять.

(Т1ри изучении каждого числа первого десятка учащиеся получают представления и о составе этих чисел. Состав чисел усваивается учащимися при объединении двух предметных совокупностей, а также разложении их на две группы и определении количества предметов в каждой группе. Например, при изучении числа 5 уча­щиеся отсчитывают 5 предметов и раскладывают их на две группы, пересчитывают предметы в каждой группе и обозначают их количе­ство соответствующей цифрой.^ратем группы предметов меняют мес­тами. На наборном полотне составляется таблица (рис. 6).

При изучении состава чисел первого десятка необходимо ис­пользовать как можно больше различных предметов. Это ускорит запоминание состава числа. Учащимся становится доступным вы­полнение упражнений вида

4=3 + П 4=П+1 4=2+П 4=П+П

При изучении состава числа в качестве дидактического мате­риала необходимо использовать пальцы рук ребенка (это «посо-124
(ни¹» всегда налицо). Надо на-гшть ребенка любое число пер-м'чо десятка представлять на ш.мьцах и раскладывать на две ц'уппы с помощью пальцев. На­пример, число 5 — это 4 и 1, 3

Д
Рис. 6
ля закрепления состава чисел наряду с пальцами надо иг пользовать работу с косточ-к.ши на первой проволоке сче­тов. Лучшему запоминанию со­става чисел способствуют уп­ражнения с частичным исполь­зованием предметных пособий и без них.

Вначале необходимо давать такие упражнения, в которых одно и.ч слагаемых воспринимается детьми наглядно, а второе они отыс­кивают по представлению. Учитель говорит: «Сосчитайте, сколько грибов я поставлю на наборное полотно». Учитель выставляет грибочки, а ученики хором считают. (Всего 5 грибочков.) «Все закройте глазки, а я сорву несколько грибов. Сколько грибов осталось?» (Дети пересчитывают и говорят результат.) — «Оста­лось 3 гриба». — «Было 5 грибов. Осталось 3 гриба. Сколько грибов я сорвала?» Учащиеся отвечают. После этого учитель по­казывает 2 гриба.

Или учитель говорит: «У меня 7 кругов. Сосчитаем их хором. Я разложу их за спиной в две руки. Кто отгадает, как я разложи­ла круги?» Учащиеся называют различные варианты состава числа 7. Кто-то из детей обязательно назовет тот вариант, кото­рый у учителя.

Важно научить детей при выполнении действий сложения и вы­читания пользоваться приемом, опирающимся на знание состава чисел. Например, надо выполнить действие 3+5=? При этом рас­суждения проводятся так: «Из 3 и 5 состоит число 8, значит, 3+5=8». Пример: 8—3=? «Число 8 состоит из 3 и 5. Если от 8 от­нять 3, то останется 5, значит, 8—3=5». Пример: 8—5=? «8 состо­ит из 5 и 3. Если от 8 отнять 5, то останется 3. Значит, 8—5=3». Пользоваться этим вычислительным приемом могут успешно толь­ко те учащиеся, которые хорошо знают состав чисел.

125

Важно систематически повторять с учащимися состав 41 Например, отсчитать 8 кубиков и разложить их несколько рг две кучки, а потом записать: 8=4+4, 8=5+3, 8=3+5, 8=( 8=2+6, 8=7+1, 8 = 1+7. К концу учебного года учащиеся д ны хорошо знать (выучить наизусть) таблицу сложения чис пределах 10. Эту таблицу можно составить по постоянному вч му слагаемому или по постоянному первому слагаемому.

Очень полезны упражнения на решение четверок примере сложение и вычитание с одинаковыми числами: 6+3, 3+6, 9 9-6.

Необходимо сопоставление примеров, определение их взаг связи, выявление признаков сходства и различия. * Школьники с нарушением интеллекта с большим трудом улавли­вают связь между сложением и вычитанием. Понимание этой связи достигается только практически. Учитель начинает демонстрацию множеств предметов), К четырем красным кубикам присоединяется 3 зеленых кубика. Кубики пересчитываются. Записывается: 4+3=7. Если из всех кубиков удалить зеленые кубики, останутся красные кубики. Записывается: 7—3=4. Затем, наоборот, из всех кубиков удаляются красные, остаются зеленые. Записывается: 7—4=3.

Необходимо чаще для отыскания ответа при вычитании отсы­лать учащихся к таблице сложения. Например, при решении при­мера 7—3 учащиеся должны в таблице сложения отыскать пример 3+4=7. Полезно решать сразу три примера 3+4, 7—3, 7—4, сопоставляя их. По примеру на сложение 5+2=7 учитель также учит детей составлять и решать два примера на вычитание с теми же числами: 7—2, 7—5.

Решение и сопоставление подобных примеров, а впоследствии и составление по одному примеру на сложение других трех, не только способствует осознанию взаимосвязи между действиями и запоминанию табличного сложения и вычитания, но и играет ог­ромную корригирующую роль. Анализ, сравнение будят мысль ребенка, заставляют его сознательно подходить к выполнению действий. Надо помнить о том, что ученик 1-го класса, как бы много подобных упражнений он ни выполнял, не вскроет заложен­ных в этих примерах зависимостей. Учитель своими заданиями по выделению признаков сходства, различия, организацией наблюде­ний над изменением компонентов действий способствует активи­зации мыслительной деятельности, преодолению косности и фор­мализма в знаниях.

126


|же в 1-м классе при изучении чисел первого десятка важно тить внимание учащихся на то, что складывать можно любые и, а вычитать — только из большего числа меньшее, что лть пример вида 3—4 нельзя. Если учитель не обратит внима-умственно отсталых школьников на это, то они допускают 5ки и при решении и при составлении примеров на вычита-нычитают из меньшего числа большее, составляют примеры 5-7=2.

1ри выполнении действий сложения и вычитания в пределах Иного числа вводится решение примеров с отсутствующим ком-Тин к-нтом. Его обозначают точками, рамками, знаками вопросов и . д., например: П+1=3, 4+...=6, ?-2=4, 6-?=2.

•пакомство с нулем проводится после изучения чисел в преде-5. Подготовка ведется на предметных пособиях, потом на , .инках и, наконец, на числах. Например, учащимся предлага-•••ivя построиться у доски (вызываются 3 человека). «Сколько учеников стоит у доски? — спрашивает учитель. — За парту сядет Надя. Сколько осталось? (Осталось 2 ученика.) За парту сядет Леня. Сколько учеников осталось? (Остался 1 ученик.) Сядет за парту Сережа. Сколько учеников осталось у доски? (Не осталось ни одного ученика.)». Учитель объясняет, что когда не осталось ни одного ученика, то можно сказать, что остался нуль учеников.

Запишем 1 — 1=0 (отсутствие предметов обозначают циф­рой 0). Решаются еще примеры, когда разность равна ОС^

Нуль сравнивается с единицей. Устанавливается, что нуль меньше единицы, а единица больше нуля, поэтому нуль должен стоять перед единицей. Однако учитель должен помнить, что нуль не относится к натуральным числам. Поэтому ряд натуральных чисел должен начинаться с единицы.

Вводить число нуль (0) в качестве вычитаемого, а потом и слагаемого следует на большом числе упражнений. Смысл дейст­вий с нулем будет лучше понят учащимися, если нуль в качестве вычитаемого и нуль в качестве слагаемого будет вводиться не­одновременно. Затем проводятся упражнения на дифференциацию примеров, в которых нуль будет слагаемым и вычитаемым.

Упражнения на дифференциацию должны включать все воз­можные сочетания, например: 1 — 1, 2—2, 5—5, 1—0, 2—0, 3—0, 1+0, 0+3, 0+0, 0-0 и т. д.

В 1-м классе после знакомства с числами от 1 до 5 учитель использует в своей речи названия компонентов и результата дей­ствия сложения.

127

Закреплению действий сложения и вычитания способствуют составление примеров с данным ответом на сложение и вычн такие (например"^

разложение любого числа на два слагаемых (например, 8=... + ..., 10=... + ...);

дополнение любого однозначного числа до данного числа или до 10.

Полезно показать учащимся и зависимость изменения сум мм от изменения слагаемых, а также изменения остатка от изменении уменьшаемого.

Учитель должен обращать внимание учащихся на то, что сумма всегда больше каждого из слагаемых (или равна ему), а остаток всегда меньше уменьшаемого (или равен ему). Уменьшаемое боль­ше или равно вычитаемому, в противном случае вычитание произ­вести нельзя.

Примеры с тремя компонентами следует сопоставлять с приме­рами, имеющими два компонента, выявлять их различие. Учителю следует помнить о том, что умственно отсталые первоклассники примеры с тремя компонентами часто решают так же, как с двумя, т. е. выполняют одно действие и сразу записывают ответ, считая, что решение примера закончено, например: 4+2—3=6. Предупреждению подобных ошибок способствует приучение уча­щихся к планированию предстоящей деятельности. Этому способ­ствует постановка перед выполнением арифметических действий вопросов вида: «Прочитай пример. Сколько действий надо выпол­нить? Какое 1-е действие? Какое 2-е действие?» Затем требова­лось от учащихся рассказать последовательность предстоящих операций. Например: «В примере надо сложить (прибавить) и вычесть. Сначала я буду складывать (прибавлять), потом вычи­тать, запишу ответ». Можно разрешить на первых порах писать результат первого действия над знаком действия, например: 5+4—2 = 7. Это один из приемов самоконтроля, к которому следу­ет готовить учащихся с 1-го класса. Они должны приучаться к проверке правильности решения примеров.