Методика преподования математики. Предисловие рецензенты доктор педагогических наук, профессор Н. М. Назарова кандидат педагогических наук В. В. Эк Перова М. Н
 Скачать 4.24 Mb.
|
0,243
9,143СРАВНЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ Начинать сравнение десятичных дробей следует с дробей со „аменателем 10, например 0,3 и 0,5. Сначала нужно каждую из тих дробей показать на метровой линейке, разделенной на деци-||етры. Известно, что 1 дм — это 0,1 м 9 дм<5 дм, значит, 3 дм — это 0,3 м 0,3 м<0,5 м 5 дм — это 0,5 м 0,3<0,5 Далее следует каждую из этих дробей сравнить с помощью любого отрезка (рис. 28). 0,3 0,5 Рис. 28 Легко сравнить эти десятичные дроби, если записать их со 5 3 знаменателями: ух- и -щ. Как сравнить обыкновенные дроби с 5 3 одинаковыми знаменателями, учащиеся знают: -|ф>-щ- После рассмотрения еще нескольких пар десятичных дробей на конкретных примерах можно подвести учащихся к выводу: из сравниваемых десятичных дробей та дробь больше, у которой число целых больше; если же целые равны (например, в дробях 0,3 и 0,5), то сравниваются десятые доли, и тогда та дробь больше, у которой число десятых долей больше. По аналогии с десятичными дробями со знаменателем 10 сравниваются десятичные дроби со знаменателем 100 (0,08 и 0,05) и со знаменателем 1000 (0,007 и 0,004). 3 п* 23 В качестве пособий для сравнения дробей со знаменателем I можно использовать метр, деленный на сантиметры, или квад|и деленный на 100 клеток: 1 0,008>0,005 0,08>0,05 см=0,01 м 8 см=0,08 м 5 см=0,05 м После усвоения этого материала для сравнения можно пред г. являть десятичные дроби с различными знаменателями: 0 0,7 и 0,13 0,08 и 0,1 ,08 и 3,1 7,3 и 7,119 Если учащиеся затрудняются сравнивать дроби, то следу г I прибегнуть к использованию наглядных пособий, которыми в дан ном случае служат меры длины, стоимости, массы, а также отрем ки и квадраты, или привести дроби к общему знаменателю. Срам нивать нужно равные десятичные дроби, но имеющие различное написание, например: 0,3 и 0,30. Что эти дроби равны, учащиеся могут убедиться с помощью метровой линейки или квадрата, раз деленного на 100 равных клеток. 0,3 м = 3 дм 1 Отсюда следуеТ1 что 0,3=0,30. 0,30 м = 3 дм] 0,1=0,10 (так как каждая полоса — это 0,1, а каждая клетка — это 0,01); 0,3=0,30; 0,5=0,50 и т. д. На подобных примерах учащиеся убеждаются, что десятые доли могут быть выражены в сотых и, наоборот, сотые — в десятых долях. Это закрепляется с помощью упражнений, например таких: Сколько десятых долей в 1 м? Чему равна одна десятая доля метра? Сколько сотых долей в 1 м? Чему равны 10 сотых метра? 0,1 м=0,10 м 0,1=0,10 Чему равны 4 десятых метра? Чему равны 40 сотых метра? 0,4 м=0,40 м 0,4=0,40 Сколько десятых в 0,1; в 0,10? Сколько десятых в 0,8; в 0,80? 324 Сравнение сотых и тысячных, десятых и тысячных долей про- дится так же, как сравнение десятых и сотых долей. На кон- |тных примерах (с мерами длины, стоимости, массы), а затем и 1тем отвлеченных рассуждений учащиеся убеждаются, что, на- ВИмер, 0,1=0,10=0,100; 0,7=0,70=0,700 и т. д. и, наоборот, [10=0,1; 0,70=0,7 и т. д. Учитель обращает внимание учащихся на то, что нули, приписные в долях дроби справа от значащей цифры, не влияют на Ьобь. Отсюда можно подвести учащихся к понятию о сокраще-]|и десятичных дробей. Сокращение десятичных дробей На примерах и практических упражнениях с метровой линей-ОЙ, квадратом, разделенным на 100 равных квадратов и 10 рав-ых полос, учащиеся убедились, что если дробь, например 0,30, вписать без нуля справа, т. е. 0,3, то дробь не изменится, но она римет более простой вид: 0,30=0,3. Запишем 0,30 со знаменате- 30 3 ем: -Г7Т7Г. Сократим эту дробь на 10, получим дробь -пг=0,3. ^ Допустим дана дробь 1,70. Эту дробь учащимся можно покапать на рулетке: 1 м 70 см, или 1,70 м, но это и 1 м 7 дм, т. е. 71,7 м, значит, 1,7 м=1,70 м, а теперь эти дроби запишем без наименований 1,70=1,7. Учащиеся еще раз убеждаются, что если в десятичной дроби отбросить 0 после значащей цифры, то величина этой дроби не изменяется. Далее объясняем сокращение десятичной дроби, опираясь на знания учащихся о сокращении обыкновенной дроби. Допустим, надо сократить дробь 1,70. Вначале учащиеся записывают эту дробь со знаменателем; а затем сокращают ее: 1,70=1-^=1-^=1,7; 1,70=1,7; 4,500=4,5; 72,010=72,01. Следовательно, отбрасывая один нуль после значащей цифры, мы сокращаем дробь на 10 (соответственно объясняем, что если отбрасываются два нуля, то дробь сокращается на 100: 0,100=0,1, так как -^=-^=0,1. Приведение десятичных дробей к общему знаменателю Учащиеся уже умеют сравнивать десятичные дроби, знают правило сравнения дробей по разрядам, но легче сравнивать дроби тогда, когда они выражены в одних и тех же десятичных долях, т. е. имеют 325 общий знаменатель." "Например, дроби 0,50 и 0,35 имеют общий менатель 100: 0,50>0,35, так как 50 сотых больше 35 сотых, удобства вычислений дроби также выражают в одинаковых до, т. е. приводят к наименьшему общему знаменателю. Учащиеся знают, что нуль, приписанный справа, дроби не меняет, т. е. 0,3=0,30=0,300. Увеличивая числитель, мы одмо| менно во столько же раз увеличиваем знаменатель. Допустим, даны две дроби 0,2 и 0,40, их надо выразить в один! вых долях. Это значит, что дробь 0,2 надо выразить в сотых дол 0,2=0,20. Дроби 0,20 и 0,40 имеют одинаковый знаменатель I Значит, надо уравнять после запятой число знаков (цифр) путем п писывания нулей справа. Так же выражают в одинаковых дс^ дроби 5,6 и 0,75. Общий знаменатель этих дробей 100. Дроби 5, 0,75 теперь будут выглядеть так: 5,60 и 0,75. В целях дифференциации понятий выразить дроби в одина вых долях и выразить дроби в более крупных долях предлагаю' упражнения вида:
3) сократить дроби: 10,80; 10,830; 14,10; 15,040; 80,< 71,060; 20,700. Запись чисел, полученных при измерении величин, в виде десятичной дроби В быту, в учебных мастерских и на производственных предприятиях учащимся приходится сталкиваться с выражением чисел, обозначающих длину, массу, стоимость и другие величины, десятичной дробью и наоборот. Начать изучение этой темы следу ет с выражения мер длины стоимости и массы десятичной дробью и наоборот. Например, 1 дм — это одна десятая доля метра, следовательно, 1 дм=0,1 м. На основании этого можно составить! такую табличку:
15 дм=1,5 м, так как 10 дм — это целый метр. По аналогии с этим можно провести рассуждения и записать десятичными дробями числа, выраженные в других мерах. Например: 326 1 ' 1 к.=0,01 р. 2 к.=0,02 р. 15 к.=0,15 р. 125 к. = 1,25 р. г=0,001 кг 5 г=0,005 кг 18 г=0,018 кг 235 г=0,235 кг При записи чисел, обозначающих длину, стоимость, массу и др., десятичной дробью следует соблюдать определенную последовательность, учитывая степень трудности выражения этого числа десятичной дробью. Вначале следует предлагать учащимся числа, выраженные одной единицей мер длины, стоимости, массы и др., а затем — двумя, причем вначале единичное отношение мер должно равняться 10. Например: 3
7 дм 5 см=7,5 дм 1 см 8 мм=1,8 см и т. д. Затем надо брать такие числа, где единичное отношение мер равно 100. Например: 1 1 м 12 см=1,12 м 8 р. 75 к.=8,75 р. 3 ц 8 кг=3,08 ц см=0,01 м 5 к.=0,05 р. 25 к.=0,25 р. Наконец, берутся такие числа, где единичное отношение мер равно 1000. Например: 1
Особое внимание обращается на такие случаи записи чисел, обозначающих длину, стоимость, массу и др., десятичной дробью, в которых в десятичной дроби десятичные доли разряда равны нулю. Например, при записи десятичной дробью следующих чисел: 8 к., 5 р., 6 к., 3 м 4 см, 7 км 80 м, 8 т 30 кг. Записывается так: 8 к.=0,08 р., так как 1 к.=0,01 р. 5 р. 6 к.=5,06 р.; 3 м 4 см= =3,04 м, 7 км 80 см=7,080 км=7,08 км; 8 т 30 кг=8,030 т=8,03 т. Запись десятичной дроби числами, полученными от измерения величин В практике нередко требуется десятичную дробь записать в виде целого числа с одним или двумя наименованиями мер. Чтобы учащиеся могли выполнить это преобразование, необходимо использование наглядных пособий и соблюдение определенной последова- 327 тельности. Сначала следует вспомнить соотношение единиц мер рассмотреть те десятичные дроби, которые имеют знаменатель 10,| 1 1 м=10 дм 0,1 м=1 дм 0,5 м=5 дм 1,7 м=1 м 7 дм дм=10 см 0,1 дм = 1 см 0,3 дм=3 см 10,4 дм=10 дм 4 см Затем рассматриваются дроби со знаменателями 100, 10001 т. е. с сотыми и тысячными долями. Например: 0,8 р.=80 к.| 2,5 м=250 см; 0,3 кг=300 г. ДЕЙСТВИЯ НДД ДЕСЯТИЧНЫМИ ДРОБЯМИ Сложение и вычитание десятичных дробей Изучение сложения и вычитания десятичных дробей опирается на знание соответствующих действий с целыми числами. Изучать действия сложения и вычитания целесообразно парал лельно, т. е. после каждого случая сложения давать соответствую щий по трудности случай вычитания Применение наглядных пособий и дидактического материала при изучении арифметических действий с десятичными дробями ограничено. Средством наглядности служит сама запись арифметических примеров, особенно запись в столбик. Итак, прежде чем знакомить учащихся со сложением и вычитанием десятичных дробей, необходимо повторить сложение и вычитание целых чисел и обыкновенных дробей. Последовательность и приемы вычисления 1. Сложение целого числа с десятичной дробью: 3+0,5; 4+0,13; 15+1,075. 2. Вычитание целого числа из десятичной дроби: 7,5—4; 7,85—3. Действия в обоих случаях выполняются устно (если целые числа небольшие). До сознания учащихся необходимо довести, что целые складываются с целыми или из целого числа вычитается целое, а дробная часть не изменяется. В этом случае можно сопоставить сложение целого числа с обыкновенной дробью: 3+0,5 и 3 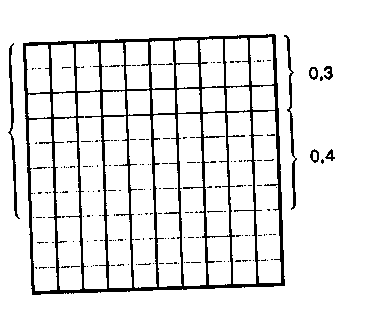 0,7 . Сложение и вычитание десятичных дробей с одинаковым числом знаков без перехода через разряд: 0,3+0,4 0,14+1,25 7,4-1,3 3,42-1,31 3,124+7,835 4,356-2,135 Д Рис. 29 ействия сложения и вычитания можно проиллюстрировать на метровой линейке, разделенной на дециметры и сантиметры, или на квадрате (рис. 29), разделенном на 10 равных полос и 100 клеток. 0,3+0,4=0,7 0,7-0,4=0,3 Учащиеся должны уяснить, что действия над десятичными дробя ми выполняются по аналогии с действиями над целыми числами, т. е. складываются и вычитаются одноименные разрядные единицы или доли единицы. Если складываются и вычитаются десятичные дроби, число знаков в которых не превышало двух, то действие выполняется устно, если число знаков выше двух, то действие запи сывается в столбик. Важно провести аналогию между записью в столбик примеров на многозначные числа и десятичные дроби и показать сходство и различие в записи и приемах вычислений: . 3456 3,456 17285 17,285 + 4243 + 4.243 | ||||
| 2,745 1,960 | .3,75 + 4,25 Й.ОО | Ю 10 _ 8,00 3,43 | ||
| 0,785 |
7699 7,699 8142 8,142
4. Сложение и вычитание десятичных дробей с разным числом знаков без перехода через разряд:
0
3,7+0,235 3,935-3,7
3,7+1,21 4,91-3,7
,71+5,246 5,956-0,71
При решении примеров такого вида учащиеся допускают ошибки, складывая или вычитая доли разных разрядов. Поэтому на первых порах следует приводить компоненты к общему знаменателю, приписывая нули справа: 3,935—3,7 записывается так:
3,935
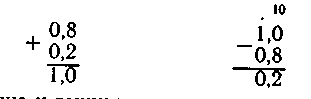и вычитание десятичных дробей с переходом че|