Дисс.-Проектирование-системы-заданий-как-условие-технологизации-. Проектирование системы заданий как условие технологизации учебного процесса в системе непрерывного образования ( на примере математики для экономического бакалавриата)
 Скачать 3.11 Mb. Скачать 3.11 Mb.
|
|
Использование Excel при изучении основ теории вероятностей и математической статистики Тампишева С.Б., старший преподаватель Казахского финансово-экономического института, г.Семипалатинск, Республика Казахстан Высшее образование и наука становятся глобальным фактором общественного развития, выдвигаются в число наиболее важных национальных и общемировых приоритетов, выступают в качестве важнейших компонентов культурного, социального и экономически устойчивого развития людей, сообществ, наций[1]. В докладе ЮНЕСКО «Высшее образование в XXI веке: подходы и практические меры» (1998г.) отмечалось, что «в сфере высшего образования наблюдается теснейшее сближение, если не общность проблем, тенденций, задач и целей, заставляющих забывать о национальных и региональных различиях и специфике»[2]. Сложившиеся в настоящее время социально-экономические и социально-культурные условия требуют подготовки специалиста, конкурентоспособного на рынке труда. Для успешного функционирования специалиста в высокотехнологическом обществе необходимо постоянное пополнение багажа знаний, умений и навыков. Непрерывное образование- необходимость и требование современной научно-технической цивилизации. Главная задача высшей школы- поднять профессиональную и социальную компетентность выпускников вузов, научить их ориентироваться в потоке постоянно меняющейся информации, мыслить самостоятельно, критически и творчески. Сегодня это невозможно без овладения студентами знаниями, умениями, навыками использования информационных технологий в сфере будущей профессиональной деятельности. К настоящему времени исследователи пришли к единому мнению, что информационные технологии должны разрабатываться с учетом классических дидактических требований: принципа научности, доступности и посильной трудности, систематичности и последовательности, прочности усвоения, наглядности, связи теории с практикой, сознательности и активности (самостоятельности), принципа коллективного характера обучения и учета индивидуальных особенностей обучающихся, однако применительно к новым информационным технологиям они имеют свою специфику [3]. ПЭВМ наиболее полно удовлетворяет дидактическим требованиям и позволяет управлять процессом обучения, максимально адаптировать его к индивидуальным особенностям обучаемого. Знания, полученные при компьютерном обучении, выступают в познавательной деятельности в качестве средства решения профессиональных задач деятельности специалиста. Также исследователи выделяют возможные направления включения компьютера в процесс учебно-познавательной деятельности обучаемых: диагностика, обучающий режим, отработка умений и навыков при решении задач после изучения темы, моделирование сложных процессов, графическая иллюстрация изучаемого материала, работа с базами данных [4]. Остановимся на применении табличного процессора Microsoft Excel при изучении элементов теории вероятностей и математической статистики в курсе математики для экономистов. Курс математики в системе подготовки экономистов является основой для изучения таких дисциплин как эконометрика, статистика, микроэкономика, макроэкономика, а математические методы исследуются во всех областях знаний. В процессе обучения математике у студентов вырабатываются навыки исследовательской работы, формируются приемы умственной деятельности, развивается интеллект, т. е. формируется личность будущего специалиста с необходимыми профессионально значимыми качествами. Применение математического аппарата теории вероятностей и математической статистики позволяет получать наиболее вероятные количественные значения экономических показателей, устанавливать связь между различными случайными параметрами и принимать обоснованные решения в экономике. В настоящее время математико-статистические методы широко внедрились в жизнь, благодаря персональным электронно-вычислительным машинам. Статистические программные пакеты сделали эти методы более доступными и наглядными, так как трудоемкую по расчету различных статистик, параметров, характеристик, построению таблиц и графиков в основном стал выполнять компьютер, а исследователю остается главным образом творческая работа: постановка задачи, выбор методов ее решения и интерпретация результатов. Существует множество различных пакетов программ по работе со статистическими данными, но наибольшее распространение в деловой сфере получил табличный процессор Microsoft Excel. Он включает в себя программную надстройку «Пакет анализа» и библиотеку из 83 (в среде Microsoft Excel 2000) статистических функций, 50 математических функций, которые позволяют автоматизировать расчеты, а также на их основе получить графическую интерпретацию. При изучении основных понятий и теорем теории вероятностей можно использовать, например, такие функции Excel как: экспонента, степень, факториал, перестановки, число комбинаций, вероятность. Изучая случайные величины и их характеристики, можно использовать, например, такие статистические функции как дисперсия, доверительный интервал, медиана, мода , различные виды распределений случайных величин и др. Кроме того, в дальнейшем, при изучении эконометрики и статистики, предоставляется широкий выбор других статистических функций. Рассмотрим использование Excel при изучении различных видов распределений дискретных и непрерывных случайных величин. При работе со случайными величинами на лекционных занятиях студентов знакомят с понятием случайной величины, законами ее распределения, математическим ожиданием, дисперсией. Формируются вероятностные модели биномиального распределения, распределения Пуассона, геометрического и гипергеометрического и других распределений, во время практических занятий эти понятия закрепляются и отрабатываются. Задания, выполненные на компьютере, помогут вывести обучающихся на более высокий уровень усвоения знаний и умений, и сопровождаться значительной экономией времени. При рассмотрении законов распределения, например, нужно обратить внимание на сферы их использования. При построении графиков функций сравнивать их кривые, анализировать, делать выводы. Рассмотрим задание на биномиальное распределение: Задание 1. Построить с помощью программы Excel, многоугольник биномиального распределения для следующих параметров: n=10; p=0,5; q=0,5; n=10; p=0,1; q=0,9; n=20; p=0,3; q=0,7; n=20; p=0,7; q=0,3; Используется статистическая функция БИНОМРАСПР: 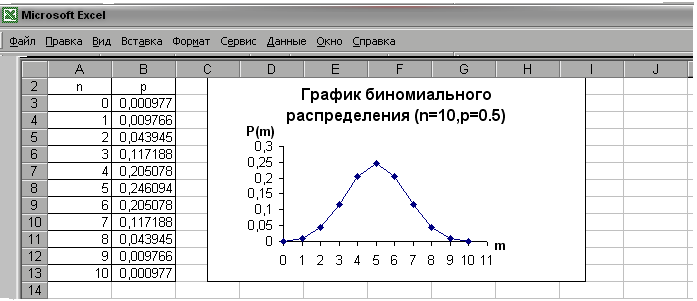 Рис.1 Многоугольник биномиального распределения ( n=10, p=0,5) Рис.1 Многоугольник биномиального распределения ( n=10, p=0,5)Изменяя параметры распределения, проследить как изменяется контур многоугольника распределения. Задание 2. Работа уличного агента по приглашению потенциальных покупателей тайм-шер считается удовлетворительной, если по его приглашению за день на презентацию придет более 10 покупателей. Считая, что вероятность того, что лицо, к которому агент обратится с предложением, с вероятностью 0,1 придет на презентацию, вычислить вероятность того, что работа агента будет признана удовлетворительной, если агент обратится с предложением к 40 прохожим. Для задачи необходимо составление компьютерной модели, выполнение громоздких расчетов с помощью функции БИНОМРАСПР. Для закрепления распределения Пуассона можно предложить задание 3. Задание 3. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени Т равно 0,002. Найти вероятность того, что за время Т откажут ровно k элементов. Построить график распределения вероятности k=0;1;2;3;4;5;6;7. Используется функция ПУАССОН: 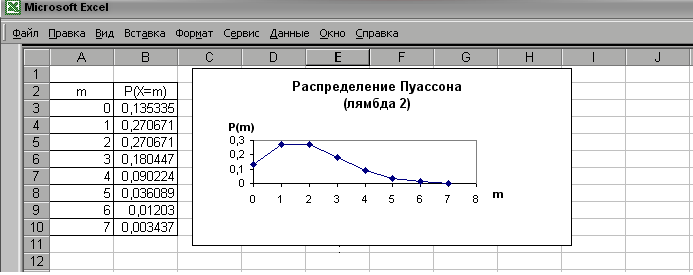 Рис.2 Многоугольник распределения Пуассона (=2) После построения графика целесообразно поставить вопрос: от какого параметра зависит распределение Пуассона? Задание 4 и 5 на гипергеометрическое распределение, выполнение расчетов и построение графика. Задание 4. В лотерее “Спортлото 6 из 45 ”денежные призы получают участники, угадавшие 3, 4, 5 и 6 видов спорта из отобранных случайно 6 видов из 45. Найти закон распределения случайной величины Х- числа угаданных видов спорта среди случайно отобранных шести. Какова вероятность получения денежного приза? Найти математическое ожидание и дисперсию случайной величины Х. В задании 4 строится модель, через функцию ГИПЕРГЕОМЕТ выполняются громоздкие вычисления для ряда этого распределения. Задание 5. Построить графики гипергеометрического распределения для следующих значений параметров: N=200; M=25; n=7; N=200; M=50; n=10 Нормальный закон распределения применяется в заданиях 6 и 7. Задание 6. Построить кривую Гаусса для: а) а=2; =2; б)а=2; =1; в)а=2; =0,5. Сделать выводы по графикам. Найти площадь под каждой кривой Гаусса. Эта задача подразумевает несколько этапов решения, процесс построения кривой , анализ полученных результатов, их геометрическую интерпретацию. Задание 7. Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина Х с параметрами а=173, а) выражение плотности вероятности и функции распределения случайной величины Х; b) доли костюмов 4-го роста (176-182 см) и 3-го роста (170-176см), которые нужно предусмотреть в общем объеме производства для данной возрастной группы; с) квантиль В задании 7 необходимо построить модель нормального распределения, вероятность попадания в интервал, применить правила нахождения квантиля . Задание 8. Непрерывная случайная величина Х распределена по показательному закону, заданному при Используется функция ЭКСПРАСП : 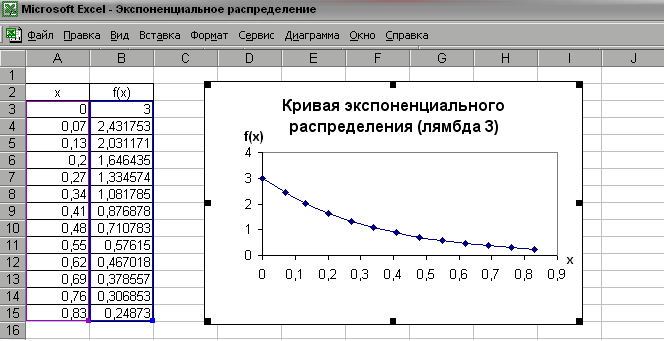 Рис. 3 График плотности экспоненциального распределения (=3) 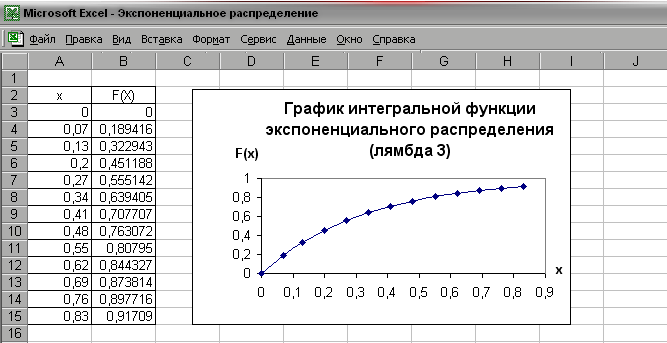 Рис.4 График интегральной функции экспоненциального распределения (=3) Для решения задач на компьютере преподаватель выполняет отбор заданий для закрепления новых понятий и навыков поэтапно, различной степени сложности, а также позволяющие изучить их в динамике. Содержание заданий требует включения не только фундаментальных положений науки, но и вопросы, связанные с перспективами ее развития, также должно способствовать систематизации знаний. Необходимо использовать богатые иллюстрационные графические возможности компьютера для представления в наглядной форме некоторого процесса и его изучения. В процессе решения задач формируется их графическое представление, анализируются различные ситуации, строятся компьютерные модели, автоматизируются непростые расчеты. Таким образом, компьютер служит инструментом для решения задач, в том числе профессионально направленных . Исследователи считают, что применение информационных технологий существенным образом преобразует мыслительную деятельность человека [6]. Формируется не только логическое, но и критическое мышление - качества, необходимые для выработки нового стиля мышления, при этом повышается общий уровень интеллектуальной деятельности. . Современный специалист без знания компьютера и компьютерных технологий не готов к реальной жизни не только профессионально, но и психологически. Студент-первокурсник с помощью Excel делает первые статистические расчеты при изучении теории вероятностей и математической статистике, в дальнейшем он продолжит эту практику при освоении других базовых и специальных дисциплин. Информационная культура специалиста является одной из составляющих профессионализма, помочь овладеть ее - важнейшая задача высшей школы. Таким образом, педагогически обоснованное использование информационных технологий в учебном процессе вузов обеспечивает заинтересованное повышение конкурентоспособности молодых специалистов на рынке труда. Литература: 1. Закон Республики Казахстан «Об образовании» от 7 июня 1999 года, №389-1 //Казахстанская правда. 11 июня.1999, № 147-148. 2. Heyn Michael, Katrina Lythoe and Charles Meyers,1999. «Education and Economic Development: Sustainability. Threshold and Equity. Proceedings of the Third UNESCO-ACEID International Conference on Educational Innovation for Sustainable Development». UNESCO: Bangkok, Thailand. 3. Сережкина А.Е., Садыкова В.А. Обучение в новой информационной среде: психолого-педагогические особенности//Высшее образование сегодня. - 2004. -.№1. - с.54-59. 4. Бекбаева З. Роль и функции средств информационной технологии в активизации самостоятельной учебно-познавательной деятельности учащихся.// Поиск, серия ест. наук. -2001. -№6, - с.113-119. 5. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2006.-573 с. 6. Тихомиров О.К. Бабанин Л.Н. ЭВМ и новые проблемы психологии. М.: Изд-во Моск. ун-та, 1986. ЗАДАНИЯ КАК средство технологизации учебного процесса В реальном учебном процессе технология обучения – это способ реализации содержания обучения, предусмотренного учебными программами, представляющий систему форм, методов и средств обучения, обеспечивающую наиболее эффективное достижение поставленных целей. При разработке технологий обучения, по мнению А.Я.Савельева, первостепенным является определение содержания обучения, предусмотренного учебным планом и учебными программами. Исходя из этого, формируются приоритетные цели, на которые ориентируется учитель. Технологизация процесса обучения требует : переформулировать идеал (глобальную цель) в диагностическую цель; разбить новую диагностическую глобальную цель на этапы и определить диагностические цели для каждого из этапов (отрезков) обучения. После определения содержания и постановки целей начинается непосредственно процесс разработки технологии обучения по этапам: I этап: Организация учебного материала. На первом этапе сообразно с поставленными целями обучения производятся следующие операции: отбирается наиболее значимый учебный материал; происходит его структурирование; идет отбор соответствующих примеров и доказательств; отбираются задачи, задания и упражнения, направленные на достижение поставленной цели. II этап: Выбор форм организации учебного процесса. Виды учебных занятий остаются традиционными, но, в зависимости от поставленных целей отбираются именно те формы организации учебного процесса, которые максимально реализуют эту цель. III этап: Выбор методов обучения. На данном этапе из всех существующих методов обучения отбираются только те, которые также будут работать на осуществление поставленной цели обучения. Например, для формирования активности личности в обучении из группы методов, направленных на первичное овладение знаниями, часто можно использовать проблемно-поисковые методы. А из информационно-развивающих методов будут преобладать методы самостоятельного добывания знаний. Из группы методов, направленных на совершенствование знаний и формирование умений и навыков будут творчески-репродуктивные методы (классификация методов обучения по А.Я.Савельеву- таблица 2.1). IY этап : Выбор средств обучения. Он характеризуется отбором наиболее эффективных средств обучения и учебного оборудования, которые также предполагают реализацию поставленных целей обучения. Исходя из конкретной направленности технологии обучения, отбираются и средства ее осуществления. (классификация средств обучения по А.Я.Савельеву -таблица 2.2.) Содержание обучения здесь теперь рассматривается как состав, структура и содержание учебной информации, предъявляемой учащимся, и как комплекс задач, заданий и упражнений, обеспечивающих достижение результатов обучения, накопление первоначального опыта. Формы обучения – устойчивые способы организации учебной деятельности учителя и учащихся, направленные на достижение планируемых результатов обучения, на воспитание и развитие учащихся в процессе обучения. Средства обучения - специально разработанные материальные, или материализованные объекты, предназначенные для повышения эффективности учебного процесса. При проектировании технологий необходимо учитывать особенности каждого обучаемого. Приоритетным сегодня является установка на самоактуализацию и самореализацию личности, в связи с чем каждый студент заслуживает собственной траектории движения по усвоению учебным материалом, отвечающей его целям, потребностям и интересам в пределах социально значимых целей (Теоретические основы построения и реализации технологий обучения. /М.Р.Ковжасарова, Н.Н.Нурахметов, .С.Кудайбергенова, Г.Д.Аульбекова –Алматы: Издательство «Мектеп»,2005.-152с.:ил) Формирование знаний по каждой дисциплине является сложным и длительным процессом, предусматривающим взаимосвязанную деятельность педагога и студента. Учитель (преподаватель) организует учебный процесс, отбирая содержание, средства и методы обучения, руководит деятельностью учащихся (студентов), обучая, развивая и воспитывая их. Известный педагог-математик Д.Пойа так сказал: «Что значит владение математикой? Это есть умение решать задачи, причем не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности». Педагогическая наука и передовая школьная практика выработали немало средств и приемов, с помощью которых учитель вовлекает учащихся в познавательную работу на уроке, активизирует процесс их мыслительной деятельности. Особое место среди них занимает обучение через задачи. Это одно из действенных средств побуждения учащихся к активной умственной работе. В ходе активной учебно-познавательной деятельности учащиеся овладевают знаниями, делают их достоянием своей личности. Задания выступают в качестве связующего звена и используются учителем как средство овладения знанием и умением, то есть формой осуществления учебно-познавательной деятельностью в условиях технологизации учебного процесса. Качество усвоения знаний и умений зависит от правильной организации деятельности учителя и учащихся, от правильного построения и включения системы заданий в учебно-познавательный процесс. Задания как одно из ведущих средств достижения намеченных целей и задач занятия многофункционально. Функции заданий зависят от целей использования их на тех или иных этапах занятия. Они могут быть использованы в ходе изучения нового материала; его закрепления; обобщения темы, раздела; систематизации знаний учащихся по отдельному разделу; при развитии основных понятий или предметных умений; при проверке достигнутых результатов обучения. Несомненно, в зависимости от специфики дисциплины задания отличаются не только содержательной основой, но и формами, способами применения на занятии, приемами использования на различных этапах учебного процесса. Эти вопросы в достаточной мере освещены в теории и методике преподавания частных предметов с учетом ведущей функции рассматриваемой учебной дисциплины. Что же означает термин « учебные задания»? Если рассматривать это понятие на уровне учебного процесса, то задания- это форма воплощения содержания образования, которое предлагается учителем и выполняется учащимися, или же фрагмент содержания образования, предложенный в виде задания. Анализ научно-педагогической литературы показал, что имеется много разных толкований этого термина. Так, в педагогическом словаре дано следующее определение: «задания учебные - разнообразные по содержанию и объему виды самостоятельной учебной работы, выполняемой учащимися по указанию учителя, неотъемлемая часть процесса обучения и важное средство его активизации (Педагогический словарь.М,,1960,Т-1,с.387). Здесь просматривается первый этап разработки технологии обучения, организации учебного материала. А.И.Уман рассматривает учебное задание как «всевозможные виды деятельности интеллектуального и практического характера, осуществляемые учеником в процессе учения» (Уман А.И. Учебные задания и процесс обучения. М.:1989 –54 с.). По-разному определяется соотношение между понятиями задачи и задания. Дидакты и методисты обычно рассматривают задачу как специфический вид задания.( Лернер И.Я. Проблемное обучение , М.,1974 г.), психологи склонны считать задание частным видом задачи. «Тот круг явлений, которые мы относим к учебным задачам, в педагогической литературе называют примерами, заданиями, упражнениями, задачами, сочинениями, самостоятельными работами и др.» (Е.И.Машбиц. Психологический анализ учебной задачи // Сов. пед-ка, 1973, №2). В.С.Аванесов в качестве основного ( родового) в теории педагогических тестов рассматривает понятие «задание», которое включает в себя задачи, упражнения, вопросы, задания в тестовой и нетестовой формах. Педагогическое задание – средство обучения и контроля уровня подготовленности, способствующее активизации, повышению качества и эффективности учебного процесса. Активизация означает оживление, усиление учебной деятельности студентов и обучающей деятельности преподавателя. Эффективность учебного процесса оценивается из соотношения цели, достигнутых результатов и проведенных затрат времени и средств, а качество учебного процесса – в зависимости от степени его соответствия заранее установленной цели, раскрываемых системой измеряемых критериев. Исходя из выше изложенного, все задания можно разделить (условно) на две группы: задания для обучения ,задания для контроля (нередко встречаются задания, применяемые и для обучения, и для контроля) (Гулидов И.Н. Педагогический контроль и его обеспечение: Учебное пособие. – М.: ФОРУМ,2005. – 240 с. – (Профессиональное образование)). Таким образом, задания выполняют обучающую и контролирующую функции, и с помошью них можно провести предварительную диагностику знаний, что также является составляющей технологии обучения. В науке исследованы различные аспекты проблемы учебных заданий. Одним из аспектов проблемы является классификация заданий, которая рассмотрена в работах И.Я .Лернера, А.И.Умана, В.Е.Володарского, Л.М.Фридмана, П.М.Эрдниева, В.О.Онищук и др. Учебные задания - это любой вид поручения учителя учащимся, заключающегося в требовании выполнить какого-либо учебные (теоретические или практические) действия. С. Ф. Жуйков, разделяя задачи на две группы, ко второй группе задач, направленных на закрепление пройденного материала, относит три вида учебных заданий: а) задания, которые требуют активизации знаний и действий применительно к тому же материалу, на котором формировалось данное понятие и действие; б) задания на применение ранее усвоенного понятия, действия, приема, закона, правила к новому материалу при условии, что учитель заранее указывает его; в) задания на применение ранее усвоенных понятий, действий и т. п. в соответствии с представляемым учебным материалом. При этом, как утверждает автор, материал может охватывать разные понятия, требовать разных действий. Такие задания, хотя и рассчитаны на воспроизведение ранее усвоенных понятий и действий, предполагают не только активность, но и определенную долю самостоятельности учащихся. (Жуйков С. Ф. Проблема активизации учащихся в психологии обучения и воспитания. « Советская педагогика », 1966, №1, стр.69-70). Но есть еще один вид заданий, который содержит учебные проблемы и рассчитан на самостоятельное изучение учащимися нового материала путем самостоятельной (в том числе и исследовательской) деятельности. Вопрос о развитии познавательной самостоятельности наиболее полно решен в работах М.Н.Скаткина, И.Я.Лернера, Э.В.Ильенкова, М.И.Махмудова. Наиболее эффективной работа бывает тогда, когда перед учащимися ставится проблема, создается таким образом проблемная ситуация. Проблемный подход способствует выработке особого качества ума- умение выделить то, что еще неизвестно. Однако наиболее эффективным средством активизации учебно-познавательной деятельности учащихся являются не отдельные задания, а их особая система. (Дайри Н. Г. Обучение истории в старших классах средней школы. М.: «Просвещение». 1966 г. с.257-267). И.Я. Лернер считает, что при обучении новому учебному материалу учащиеся проходят три уровня усвоения содержания образования: 1) восприятие и запоминание; 2) репродуктивный; 3) творческий. Для достижения каждого из этих уровней требуется выполнение определенного типа заданий. Автор выделяет следующие типы заданий: 1) задания рецептивного характера, направленные на усвоение знаний; 2) задания репродуктивного характера, направленные на применение знаний по образцу или в знакомой ситуации; 3) задания творческого характера, направленные на применение знаний в незнакомой ситуации. Кроме того, И.Я.Лернер предлагает выделить четвертый тип заданий, задания на развитие эмоционально- ценностной сферы. А.И Уманом были систематизированы существующие классификации заданий, в результате чего различные виды заданий объединены им в пять групп. В первую группу объединены виды, ориентированные на структурно-компонентный состав задания, имеющие в своей основе один из трех признаков: характер требования, состав исходных данных, способ решения. Во вторую группу автор определил задания, ориентированные на деятельность учащегося, учитывающие степень сложности деятельности, степень самостоятельности выполнения задания, языковые и речевые формы. Задания, предполагающие контроль за усвоением знаний учащихся, составляют основу заданий, ориентированных на деятельность учителя. Это различного рода проверочные, тренировочные, контрольные и так далее задания. В следующую группу объединены задания, ориентированные на содержание изучаемого материала, по их направлению на усвоение отдельных компонентов содержания образования. Это задания на усвоение знаний, формирование умений и навыков, приобретение опыта творческой деятельности и задания на приобретение опыта эмоционально-ценностного отношения к окружающему миру. Кроме того, А.И.Уман рассматривал задания в плане связи со способом структурирования знаний. Учебный материал может структурироваться методом простых единиц и укрупненных единиц. Задания данной группы в зависимости от способа структурирования содержания образования и расположения структурных единиц во времени их изучения делятся автором на мелкие и укрупненные. На наш взгляд, данная классификация учебных заданий наиболее приемлема с позиции рассматриваемой нами проблемы. В.Г.Болтянский (Б2) подразделяет задания, предлагаемые учащимся на «упражнения» и «задачи». Рассмотрим более подробно составляющие такие понятия как «упражнения», «задачи», «вопросы», т.е. подходы к этим понятиям. Что следует понимать под термином «упражнения»? В психологии упражнениями называют многократное выполнение определенных действий или видов деятельности, имеющее целью их освоение, опирающееся на понимание и сопровождающееся сознательным контролем и корректировкой. В этом определении подчеркивается целенаправленность упражнений, которые осуществляются на основе понимания и тщательно продуманного педагогического руководства. Стихийное, неуправляемое повторение действий может не привести к их усовершенствованию или приведет к механической тренировке в применении действий в стандартных условиях. Психолог В.А.Крутецкий формулирует следующие требования к упражнениям: 1) необходимо точно знать цель упражнения, знать, каких результатов нужно добиться; 2) необходимо специально следить за точностью выполнения, чтобы не закреплять ошибки, если они возникают, следить за результатами упражнений, сравнивая свои действия с эталоном, осознавать, какие успехи достигнуты и на каких недостатках следует фиксировать свое внимание, чтобы устранить их; 3) число упражнений, которое зависит от индивидуально-психологических особенностей обучаемых, должно быть достаточным для образования определенного учебного навыка; 4) упражнения не должны быть случайным набором однотипных действий. В их основе должна лежать определенная система, четко спланированная, правильная их последовательность, в частности постепенное усложнение; 5) упражнения не должны прерываться, иначе навык образуется медленно или, если он не закреплен, быстро ослабляется и даже вообще теряется. Г.И.Саранцев проблему упражнений решает на основе «концепции упражнений как явления, выступающего в обучении математике способом организации учебно-познавательной деятельности обучаемых, носителем действий, адекватных содержания обучения, средством целенаправленного формирования знаний, умений и навыков, и функционирующим как система»(Саранцев Г.И. Теоретические основы методики упражнений по математике в средней школе: автореферат докторской диссертации по методике преподавания математики. – Л.: Издательство Ленинградского пединститута. 1987 – 36 с.). Педагогическая наука и практика в последние годы значительно продвинулась в вопросе определения рациональных способов формирования учебных навыков и умений. Навыком считается выработанное на основе упражнений автоматизированное действие, являющееся компонентом умения. Умение в современной психологии определяется как использование имеющихся знаний и навыков для выбора и осуществления приемов действия в соответствии с поставленной целью. Навыки являются составными компонентами умений, они формируются на основе знания способов выполнения действия. Умения в своей основе являются творческими действиями Навыки и умения формируются на основе выполнения определенной системы упражнений, совершенствуются и закрепляются в процессе творческого их применения в изменяющихся ситуациях. Немало сделано в совершенствовании содержания упражнений, изменении соотношения репродуктивных и творческих упражнений в пользу последних, применении проблемных заданий, методике руководства работой обучаемых в процессе выполнения упражнений. Актуальной становится проблема выработки дидактической системы упражнений, предусматривающей постепенное нарастание сложности заданий и самостоятельности учащихся В.А.Онищук предлагает дидактическую систему, в которой первые задания имеют репродуктивный характер и предусматривают актуализацию ранее приобретенных знаний, чувственного и практического опыта, на которые должно опираться усвоение новых навыков и умений. Они выполняются под жестким контролем и при помощи постоянной корректировки учителя, но при этом требуют минимума самостоятельности и творчества. Переход от предшествующих видов заданий и упражнений к последующим предполагает не только постепенное нарастание трудности и сложности заданий, но и усиление самостоятельности в их выполнении и творческого подхода в их решении. Представление о последовательности упражнений и их соответствие целям и задачам обучения на различных этапах усвоения навыков и умений может дать таблица 2.3. Таблица 2.3. Последовательность упражнений в процессе усвоения учащимися навыков и умений
(Онищук В.А. Урок в современной школе: Пособие для учителей. –М.: Просвещение,1981.-191с., С.137). Данилов М А., говоря о большом значении и восприятии учебного материала, выделяет следующие их виды: упражнения, подготавливающие восприятие формулировки и доказательства нового материала; упражнения, способствующие дальнейшему осмысливанию новых терминов и формулировок; упражнения, направленные на закрепление пройденного материала. Система упражнений и задач, как отмечает М.А.Данилов и В.П.Есипов, должна приводить к тому, чтобы учащиеся безупречно применяли изученные ими понятия, правила, приемы в их творческих работах и в жизни (Данилов М.А., Есипов В.П. Дидактика. – М. АПН РСФСР.1957 г.- 331). «Все способы активизации познавательной деятельности ученика в качестве основного элемента обязательно имеют в своем составе вопрос, задачу, задание, наглядные образы или их сочетание. Суть активизации состоит в том, что при определенных условиях эти понятия являются формой выражения проблемности»- пишет М.И.Махмудов (Махмудов М.И.Проблемное обучение(основные вопросы теории). М,1975) В активизации познавательной деятельности учащихся вопросы имеют едва ли не первостепенное значение. Вопросно-ответная форма взаимодействия применялась еще в древности. Что такое «вопрос»? В «Словаре русского языка» С.И.Ожегова дается три значения слова «вопрос». Приведем два из них. Первое значение - словесная формулировка мысли, ее языковая оболочка. Второму значению присуще более глубокое содержание, отражающее какое-то непознанное явление реальной действительности. В основе второго значения лежит диалектическое противоречие между известным и неизвестным. Именно он и является источником движения мысли, дающим импульс развитию суждения. Со времен К.Д.Ушинского в дидактике считается , что ни один методический прием не является гибким, как управление познавательной деятельностью ученика путем задавания вопросов (Тихомиров О.К. Чему и как учить на уроках родного языка в начальной школе.СПб.,1911). «Вопросы, - пишет Н.Г.Дайри, - как ни один другой прием, дают возможность с наименьшей затратой времени вести самую разнообразную работу по развитию учащихся» (Дайри Н.Г. Приемы текущей проверки знаний по истории. Экспериментальные исследования по истории в старших классах средней школы.М., Изд-во АПН РСФСР, 1958) С современной точки зрения учение не сводится лишь к осмысленному усвоению и сохранению в памяти учебной информации в познании отдельных фактов и систем, оно, прежде всего, заключается в усвоении поиска и решение познавательных проблем. Понятия задача весьма многопланово. В психологической, философской литературе имеются различные трактовки этого понятия. Задачу принято считать основной структурной единицей содержания любого учебного предмета (Дифференциация в обучении математике / Г.В.Дорофеев, Л.В. Кузнецова, С.Б. Суворова, В.В.Фирсов // Математика в школе.- 1990. -№4.-с.15-21.) Для обучающегося она выступает в качестве иллюстрации теории, возможности разрешения практической ситуации, упражнения для обработки определенных методов решения и т.п.обучающему задача, прежде всего, служит способом анализа и оценки процесса и результатов и деятельности обучающихся.( Ефремов А.В. Научно-методические основы отбора, структурирования и реализации содержания математического образования в старших классах общеобразовательной школы6 Дисс.докт.пед.наук –Казань,1995 –58 с.). И педагоги и психологи считают задачу в обучении одним из важных факторов повышения познавательной и практической активности учащихся. Задача характеризуется: наличием у учащихся определенной цели, стремлением получить ответ на тот или иной вопрос, достичь желаемого результата; учетом имеющихся условий и требований, необходимых для решения задачи; применением соответствующих данной цели и условиям способов или приемов решения (Педагогическая энциклопедия. Т. I-IV. М., « Советская энциклопедия », 1965-1968 гг., т.2, стр.62 ) М.А.Данилов понимал под задачей «сознательное многократное повторение выполнение сходных действий … с целью овладения навыками»( Проблемы методологии педагогики и методы исследований./Под ред.М.А.Данилова и Н.И.Болдырева. – М.: Педагогика, 1971. –352 с.). С точки зрения А.В.Ефремова «задача - это информационная совокупность связей и зависимостей, выраженных словесно, графически или в математических формулах, составляющая определенную ситуацию, определяющую и побуждающую мысленную деятельность субъекта на нахождение путем упорядоченных действий функционального выражения неизвестных компонентов через известные» (Ефремов А.В. Научно-методические основы отбора, структурирования и реализации содержания математического образования в старших классах общеобразовательной школы6 Дисс.докт.пед.наук –Казань,1995 –58 с.). Мы, также как и А.В.Ефремов, считаем, что преподаватель ставит перед собой задачу развития познавательной деятельности и творческих способностей обучаемых. Учитель должен организовать учебный процесс так, «чтобы решение каждой задачи для учеников стало значительным событием, чтобы при решении любой задачи он проявил творческий подход в выборе методов и способов решения, чтобы каждая решенная задача была использована при решении последующих задач и оказала существенное влияние на развитие творческих качеств его личности» (Ефремов А.В. Научно-методические основы отбора, структурирования и реализации содержания математического образования в старших классах общеобразовательной школы». Дисс.докт.пед.наук –Казань,1995 –58 с.). Н.А.Менчинская, А.Ф.Эсаулов, Е.И Машбиц, В.А.Крутецкий и др. рассматривали психологические аспекты решения задач. Задачи управления учебной деятельностью или дидактические задачи в конечном счете можно свести к выбору содержания учебного предмета, метода обучения. В каждой задаче можно выделить следующие компоненты: 1) цель (требование), 2) объекты, которые входят в состав условия задачи, 3) их функции, 4) указания о способах и средствах решения (последний компонент имеет место только в некоторых задачах). В качестве объектов учебных задач выступают обычно не сами объекты окружающей среды, а некоторые знания о них, отражающие, как правило, только некоторые их свойства. Что касается их функций, то они естественно отражают прежде всего особенности связей (отношений между объектами), которые специфичны для того или иного учебного предмета. При характеристике задач нужно, прежде всего учитывать, что они являются средством достижения целей учения. Отсюда следует, что существенной характеристикой учебной задачи является ее соотношение с целью учения, а поскольку для достижения ее требуется набор задач, такое соотношение следует провести для всего набора. Анализ набора, т.е. системы, учебных задач требует их классификации, а для этого необходимо установление критериев, выделение их существенных характерных черт. ( Машбиц Е.И. Психологический анализ задачи…) В современной методической и психологической литературе принята классификация задач. По характеру требования: задачи на доказательство; задачи на построение; задачи на вычисление. По функциональному назначению: задачи с дидактическими функциями; задачи с познавательными функциями; задачи с развивающими функциями. По величине проблемности: стандартные (известны все компоненты задачи); обучающие (неизвестен один из четырех компонентов задачи); поисковые (неизвестны два из четырех компонентов задачи); проблемные (неизвестные три из четырех компонентов задачи). По методам решения: задачи на геометрические преобразования; задачи на векторы и др. По числу объектов в условии задачи и связи между ними: простые; сложные. По компонентам учебной деятельности: организационно- действенные; стимулирующие; - контрольно- оценочные.(Темербекова А.А. Методика преподавания математики: Учеб.пособие для студ.высш. учеб.заведений. – М.: Гуманит. Изд.центр ВЛАДОС, 2003. – 176с,С.74) Кроме того, различают задачи стандартные и нестандартные; теоретические и практические, устные и письменные, одношаговые, двушаговые и др., устные, полуустные, письменные и т. д. В обучении применяется большое разнообразие задач, используемых для усвоения новых знаний, повторения и закрепления, т. е. для овладения системой научных знаний. Л. В. Занков указывает на наличие таких задач, которые имеют общий характер и не привязаны к определенной теме учебной программы. Эти задачи он делит на два вида : задачи, требующие ознакомления с внешним обликом объекта, и задачи, требующие изучения связей и зависимости между явлениями (сами эти связи и зависимости не воспринимаются непосредственно). « Задачи, которые связываются в обучении, - пишет Л. В. Занков, - трактуются, как правило, только в плане усвоения знаний и навыков. Что касается развития учеников, то фигурирующие в дидактических трудах общие призывы, касающиеся необходимости работать над развитием школьников, не получают воплощения при рассмотрении учебных задач » (Занков Л. В. Дидактика и жизнь. М., « Просвещение », 1968гг., стр.99). Для достижения развития учащихся путем применения задач необходимо исследование объективных связей между задачей, способами (методами) обучения и достигаемым результатом. Исходя из того, что умственная деятельность учащихся стимулируется задачами, С. Ф. Жуйков делит их на задачи, которые характерны для процесса приобретения знаний, умений, и задачи, характерные для закрепления пройденного материала. В первую группу включаются : а) задачи на выполнение действия по образцу, которые используются при получении учащимися знаний в готовом виде; б) задачи на самостоятельное « открывание » нового, вызывающие продуктивный, творческий тип познавательной деятельности учащихся. С. Ф. Жуйков подчеркивает, что такие задачи (на выведение правил, законов, на нахождение приемов умственной деятельности и т. д.) характерны для проблемного обучения ( Жуйков С. Ф. Проблема активизации учащихся в психологии обучения и воспитания. « Советская педагогика ». 1966, №1., стр. 69). В « Педагогической энциклопедии » указывается, что решение задачи « всегда требует от учащегося не простого воспроизведения усвоенного в той форме, в какой оно использовалось в предшествующем опыте, а того или иного изменения его содержания или способа оперирования им » (Менчинская Н. А. Задача в обучении.- Педагогическая энциклопедия, т.2., стр.62). На практике решение стандартных задач требует многократного применения уже усвоенных знаний (способа решения) для обработки навыка применения определенного алгоритма решения. М.И Махмудов дифференцирует познавательную задачу, т. е. такую, решение которой приводит учащихся к новым для них знаниям и способам действия. «Мы дифференцируем понятие «познавательная задача» на проблемную задачу и непроблемную задачу по способам ее постановки учителем и по содержанию. Задача может быть проблемной и непроблемной не только по методам ее постановки, но и по содержанию. Внутренняя структура непроблемной задачи характеризуется тем, что содержание данного и искомого не ново для ученика в принципе, новым могут быть только факты (например, цифры). Сам же принципиальный способ решения, способ соотнесения данного с искомым уже известен. Если же решение задачи прежними способами невозможно и требуется новый способ решения, то это проблемная задача (по содержанию).(Махмудов М.И. Проблемное обучение) Внутреннюю структуру проблемной познавательной задачи, содержащей учебную проблему, хорошо раскрывает А. М. Матюшкин: «Проблемная задача в отличие от обычных учебных задач представляет не просто описание некоторой ситуации, включающей характеристику данных, составляющих условие задачи, и указание на неизвестное, которое должно быть раскрыто на основании этих условий. В проблемной задаче сам субъект включен в ситуацию задачи » (Матюшкин А. М. К проблеме «шага » процесса усвоения. «Новые исследования в педагогических науках ». Вып. VII., М., 1966 гг., стр.12). Следовательно, познавательные задачи, применяемые для активизации познавательной деятельности учащихся, должны иметь свойство обобщенности. Это свойство обусловлено наличием в задаче определенного уровня сложности, который определяется: а) методическим способом постановки задачи перед учащимися (например, способом ее речевой формулировки); б) проблемным содержанием задачи; в) личностным отношением ученика к поставленной задаче. Сущность применения познавательных задач в качестве способа активизации учебно- познавательной деятельности учащихся заключается в подборе системы проблемных задач и систематическом управлении ходом их решения. Сказанное вовсе не исключает применения в учебном процессе непроблемных задач, речь должна идти о рациональном сочетании тех и других. .(Махмудов М.И. Проблемное обучение.(основные вопросы теории).М.,1975) Решение математических задач играет исключительно важную роль в обучении. Эта роль определяется прежде всего тем, что конечные цели обучения предмету сводятся не только к овладению обучаемыми методами и способами решения определенной системы задач, но и тем, что через решение задач происходит усвоение предметной деятельности. Достижение полноценного результата обучения возможно при условии применений знаний к решению практических задач. При таком подходе, решение задач выступает и как цель, и как средство обучения. Решение задач служит средством формирования и развития мышления, способствует более глубокому и прочному усвоению понятий, формул, теорий, созданию условия для осуществления профессиональной ориентации, формированию умений и навыков. Решение задач выполняет определенные функции в учебно- воспитательном процессе, ибо оно приводит ко многим изменениям в знаниях, структуре деятельности и психике, решающего задачу. Абылкасымова А.,. Папышев А , рассматривая методику построения системы математических задач, выделяют следующие основные функции решения задач : вводно- мотивационная; познавательная; развивающая; воспитывающая; управляющая; иллюстративная; контрольно- оценочная. ( Абылкасымова А., А. Папышев. О методологии и методике построения системы математических задач.//Высшая школа Казахстана .№4 2002 г. с.36-38) Следует учитывать, что решение задач способствует: овладению знаниями практического применения изучаемых математических формул; формированию и развитию у учащихся межпредметных и исследовательских умений и навыков; формированию и развитию у учащихся обобщенного умения решать задачи. Рассмотрим некоторые из приведенных выше функций решения задач. |
