Вычислительная математика. Вычислительная_матиматика. Решение задач вычислительными методами. Основные понятия Погрешность
 Скачать 1.45 Mb. Скачать 1.45 Mb.
|
|
Тема 4. Приближение функций 4.1. Постановка задачи Задача приближения (аппроксимации) функций заключается в том, чтобы для данной функции построить другую, отличную от нее функцию, значения которой достаточно близки к значениям данной функции. Такая задача возникает на практике достаточно часто. Укажем наиболее типичные случаи. 1. Функция задана таблицей в конечном множестве точек, а вычисления нужно произвести в других точках. 2. Функция задана аналитически, но ее вычисление по формуле затруднительно. При решении задачи поиска приближенной функции возникают следующие проблемы. 1. Необходимо выбрать вид приближенной функции. Для приближения широко используются многочлены, тригонометрические функции, показательные функции и т. д. 2. Необходимо выбрать критерий близости исходной и приближенной функции. Это может быть требование совпадения обеих функций в узловых точках (задача интерполяции), минимизация среднеквадратического уклонения (метод наименьших квадратов) и др. 3. Необходимо указать правило (алгоритм), позволяющее с заданной точностью найти приближение функции. 4.2. Приближение функции многочленами Тейлора Пусть функция y = f(x)определена в окрестности точки a и имеет в этой окрестности n + 1 производную. Тогда в этой окрестности справедлива формула Тейлора: f(x)= c0 + c1(x – a) + c2(x – a)2 + … + cn(x – a )n + Rn(x) = Tn(x) + Rn(x), где ck = Tn(x) – многочлен Тейлора: Tn(x)= c0 + c1(x – a) + c2(x – a)2 + … + cn(x – a )n, (4.1) Rn(x) – остаточный член формулы Тейлора. Его можно записать различными способами, например, в форме Лагранжа: Rn(x)= Многочлен Тейлора (4.1) обладает свойством, что в точке x = a все его производные до порядка n включительно совпадают с соответствующими производными функции f, т. е. T В этом легко убедиться, дифференцируя Tn(x). Благодаря этому свойству многочлен Тейлора хорошо приближает функцию f в окрестности точки a. Погрешность приближения составляет |f(x) – Tn(x)| = |Rn(x)|, т. е. задавая некоторую точность > 0, можно определить окрестность точки a и значение n из условия: |   Rn(x)| = Rn(x)| = Пример 4.1. Найдем приближение функции y = sinx многочленом Тейлора в окрестности точки a = 0. Воспользуемся известным выражением для k-ой производной функции sinx: (  sinx)(k) = sin x + k sinx)(k) = sin x + kПрименяя последовательно формулу (4.3), получим: f(0) = sin0 = 0; f '(0) = cos(0) = 1; f"(0) = –sin0 = 0; …………………… f(2k-1)(0) = sin (2k – 1) f(2k)(0) = 0; f(2k+1)() = (–1)kcos Следовательно, многочлен Тейлора для функции y = sinx для n = 2k имеет вид: sinx = x – R2k(x) = (–1)k Зададим = 10 –4 и отрезок [– |R2k(x)| = Т  аким образом, на отрезке – аким образом, на отрезке –sinx = x – Пример 4.2. Найдем приближение функции y = ex многочленом Тейлора на отрезке [0, 1] с точностью = 10 –5. Выберем a = ½, т. е в середине отрезка. При этом величина погрешности в левой части (4.2) принимает минимальное значение. Из математического анализа известно, что для k-ой производной от ex справедливо равенство: (ex)(k) = ex. Поэтому (ea)(k) = ea = e1/2, Следовательно, многочлен Тейлора для функции y = exимеет вид: ex = e1/2 + e1/2(x – ½) + При этом, учитывая, что x[0, 1], получим оценку погрешности: |Rn(x)| < Составим таблицу погрешностей, вычисленных по формуле (4.4):
Таким образом, следует взять n = 6. 4.3. Интерполяция функции многочленами Лагранжа Рассмотрим другой подход к приближению функции многочленами. Пусть функция y = f(x)определена на отрезке [a, b] и известны значения этой функции в некоторой системе узлов xi [a, b], i = 0, 1, … , n. Например, эти значения получены в эксперименте при наблюдении некоторой величины в определенных точках или в определенные моменты времени x0, x1, … , xn.Обозначим эти значения следующим образом: yi = f(xi), i = 0, 1, … , n. Требуется найти такой многочлен P(x) степени m, P(x) = a0 + a1x + a2x2 + … + amxm, (4.5) который бы в узлах xi, i = 0, 1, … , n принимал те же значения, что и исходная функция y = f(x), т. е. P(xi) = yi, i = 0, 1, … , n. (4.6) Многочлен (4.5), удовлетворяющий условию (4.6), называется интерполяционным многочленом. Другими словами, ставится задача построения функции y = P(x), график которой проходит через заданные точки (xi, yi), i = 0, 1, … , n (рис. 4.1). 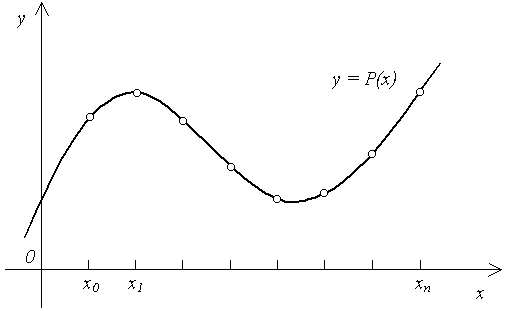 Рис. 4.1 Объединяя (4.5) и (4.6), получим: a0 + a1xi + a2x В искомом многочлене P(x) неизвестными являются m +1 коэффициент a0 , a1, a2, …, am. Поэтому систему (4.7) можно рассматривать как систему из n +1 уравнений с m +1 неизвестными. Известно, что для существования единственного решения такой системы необходимо , чтобы выполнялось условие: m = n. Таким образом, систему (4.7) можно переписать в развернутом виде: a 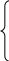 0 + a1x0 + a2x 0 + a1x0 + a2xa0 + a1x1 + a2x a0 + a1x2 + a2x ……………………………………………. a0 + a1xn + a2x Вопрос о существовании и единственности интерполяционного многочлена решает следующая теорема: Теорема 4.1. Существует единственный интерполяционный многочлен степени n, удовлетворяющий условиям (4.6). Имеются различные формы записи интерполяционного многочлена. Широко распространенной формой записи является многочлен Лагранжа Ln(x) = В частности, для линейной и квадратичной интерполяции по Лагранжу получим следующие интерполяционные многочлены: L1(x) = y0 L2(x) = y0 Пример 4.3. Построим интерполяционный многочлен Лагранжа по следующим данным:
Степень многочлена Лагранжа для n +1 узла равна n. Для нашего примера многочлен Лагранжа имеет третью степень. В соответствии с (4.9) L3(x) = 1 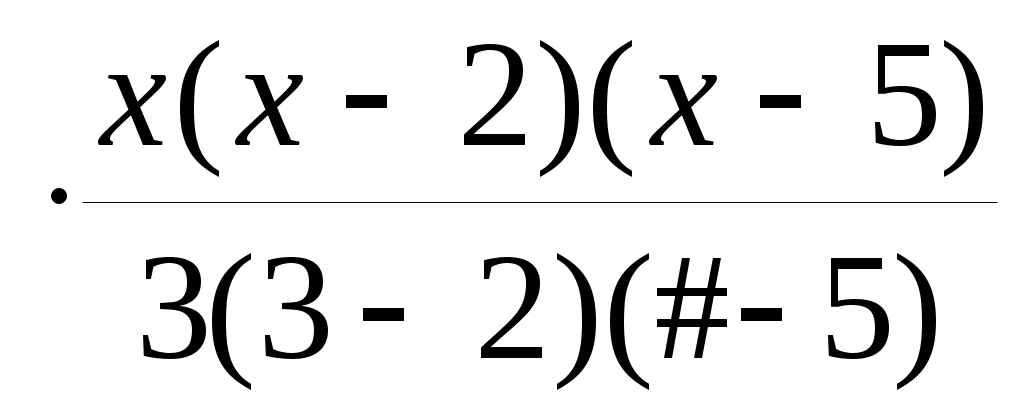 + 5 + 5Пример 4.4. Рассмотрим пример использования интерполяционного многочлена Лагранжа для вычисления значения заданной функции в промежуточной точке. Эта задача возникает, например, когда заданы табличные значения функции с крупным шагом, а требуется составить таблицу значений с маленьким шагом. Для функции y = sinx известны следующие данные.
Вычислим y(0.25). Найдем многочлен Лагранжа третьей степени: L3(x) = 0 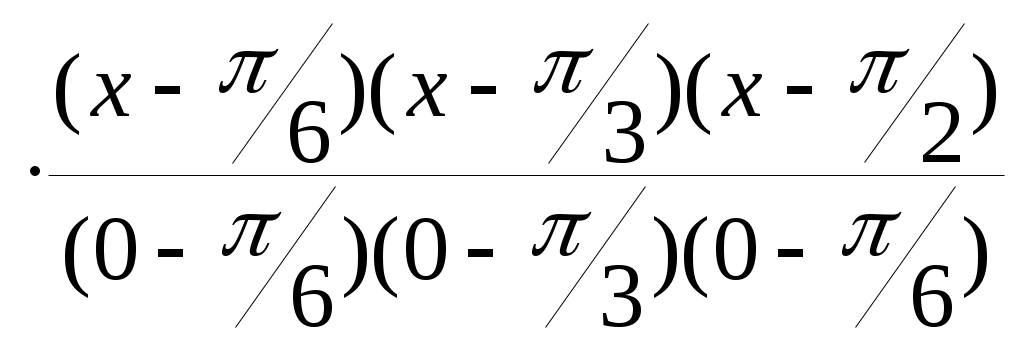 + + 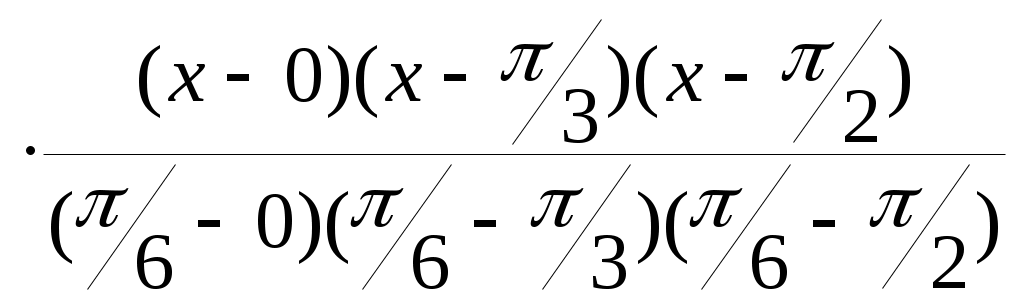 + +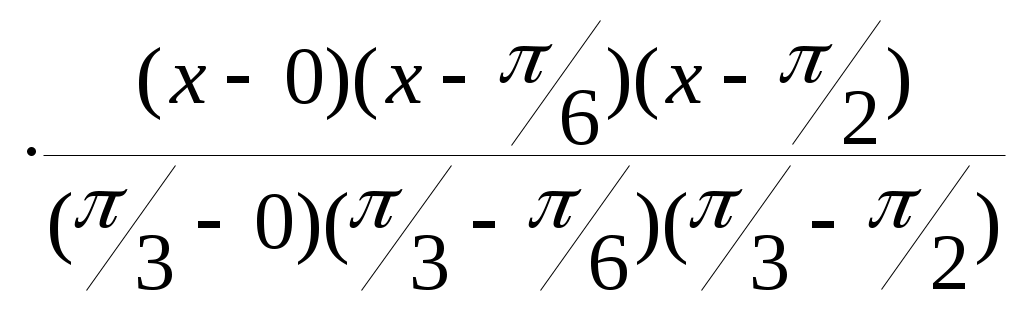 + 1 + 1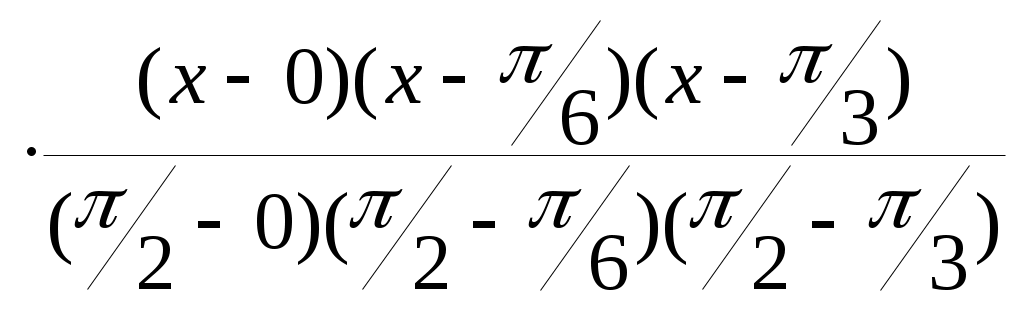 . .При x = 0.25 получим y(0.25) = sin 0.25 0.249. Погрешность интерполяции. Пусть интерполяционный многочлен Лагранжа построен для известной функции f(x). Необходимо выяснить, насколько этот многочлен близок к функции в точках отрезка [a, b], отличных от узлов. Погрешность интерполяции равна |f(x) – Pn(x)|. Оценку погрешности можно получить на основании следующей теоремы. Теорема 4.2. Пусть функция f(x)дифференцируема n +1 раз на отрезке [a, b], содержащем узлы интерполяции xi [a, b], i = 0, 1, … , n. Тогда для погрешности интерполяции в точке x [a, b] справедлива оценка: |f(x) – Ln(x)| где Mn+1= n+1(x) = (x – x0)(x – x1)…. (x – xn). Для максимальной погрешности интерполяции на всем отрезке [a, b] справедлива оценка: Пример 4.5. Оценим погрешность приближения функции f(x) = Найдем первую, вторую и третью производные функции f(x): f '(x)= M3= В соответствии с (4.9) получим оценку погрешности в точке x = 116: | Оценим погрешность приближения функции f(x) = 4.4. Аппроксимация функций. Метод наименьших квадратов В инженерной деятельности часто возникает необходимость описать в виде функциональной зависимости связь между величинами, заданными таблично или в виде набора точек с координатами (xi, yi), i = 0, 1, 2,... , n, где n – общее количество точек. Как правило, эти табличные данные получены экспериментально и имеют погрешности (рис. 2.5) 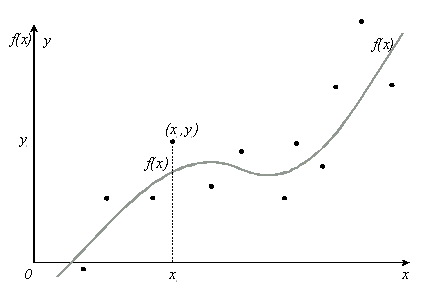 Рис.4.2 При аппроксимации желательно получить относительно простую функциональную зависимость (например, многочлен), которая позволила бы "сгладить" экспериментальные погрешности, вычислять значения функции в точках, не содержащихся в исходной таблице. Эта функциональная зависимость должна с достаточной точностью соответствовать исходной табличной зависимости. В качестве критерия точности чаще всего используют критерий наименьших квадратов, т.е. определяют такую функциональную зависимость f(x), при которой S = обращается в минимум. Погрешность приближения оценивается величиной среднеквадратического уклонения D = В качестве функциональной зависимости рассмотрим многочлен Pm(x)=a0 +a1x+a2x2+...+amxm. (4.14) Формула (4.12) примет вид S = Условия минимума S можно записать, приравнивая нулю частные производные S по всем переменным a0, a1, a2, … , am. Получим систему уравнений Систему уравнений (4.15) перепишем в следующем виде: a0 Введем обозначения: ck = Система (4.16) может быть записана так: a0ck + a1ck+1 + … + ck+mam = bk, k = 0, 1, … , m. (4.17) 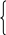 Перепишем систему (4.17) в развернутом виде: Перепишем систему (4.17) в развернутом виде:c0a0 + c1a1 + c2a2… + cmam = b0 c1a0 + c2a1 + c3a2… + cm+1am = b1 …………………………………….. (4.18) cma0 + cm+1a1 + cm+2a2… + c2mam = bm Матричная запись системы (4.18) имеет следующий вид: Ca = b. (4.19) Для определения коэффициентов ak, k = 0, 1, … , m, и, следовательно, искомого многочлена (4.14) необходимо вычислить суммы ck, bk и решить систему уравнений (4.18). Матрица C системы (4.19) называется матрицей Грама и является симметричной и положительно определенной. Эти полезные свойства используются при решении. Погрешность приближения в соответствии с формулой (4.13) составит D = Рассмотрим частные случаи m =1 и m = 2. 1. Линейная аппроксимация (m = 1). P1(x) = a0 + a1x. c0 = b0 =   c0 c1 n+1 c0 c1 n+1 C = = , c1 c2 b = (b0, b1)T = ( Решение системы уравнений Ca = b найдем по правилу Крамера: a0 = где úCú – определитель матрицы C, аúCiú – определитель матрицы Ci, полученной из матрицы C заменой i-го столбца столбцом свободных членов b, i = 1, 2. Таким образом, a0 = Алгоритм 4.1 (Алгоритм метода наименьших квадратов. Линейная аппроксимация). Шаг 1. Ввести исходные данные: xi, yi, i=0, 1, 2, ... , n. Шаг 2. Вычислить коэффициенты c0, c1, b0, b1 по формулам (4.21), (4.22). Шаг 3. Вычислить a0, a1 по формулам (4.23). Шаг 4. Вычислить величину погрешности D1 = Шаг 5. Вывести на экран результаты: аппроксимирующую линейную функцию P1(x) = a0 + a1x и величину погрешности D1. 2. Квадратичная аппроксимация (m = 2). P2(x) = a0 + a1x + a2x2. c0 = b0 =  c0 c1 c2 c0 c1 c2 C = c1 c2 c3 . c2 c3 c4 b = (b0, b1, b2)T . Решение системы уравнений Ca = b найдем по правилу Крамера: ai = где úCú – определитель матрицы C, аúCiú – определитель матрицы Ci, полученной из матрицы C заменой i-го столбца столбцом свободных членов b. úCú = c0c2c4 + 2c1c2c3 – c   b0 c1 c2 b0 c1 c2 úC1ú = b1 c2 c3 = b0c2c4 + b2c1c3 + b1c2c3 – b2c b2 c3 c4   c0 b0 c2 c0 b0 c2 úC2ú = c1 b1 c3 = b1c0c4 + b0c2c3 + b2c1c2 – b1c c2 b2 c4   c0 c1 b0 c0 c1 b0 úC3ú = c1 c2 b1 = b2c0c2 + b1c1c2 + b0c1c3 – b0c c2 c3 b2 a0 = Алгоритм 4.2(Алгоритм метода наименьших квадратов. Квадратичная аппроксимация). Шаг 1. Ввести исходные данные: xi, yi, i=0, 1, 2, ... , n. Шаг 2. Вычислить коэффициенты c0, c1, c2, c3, c4, b0, b1, b2, по формулам (4.25), (4.26). Шаг 3. Вычислить úCú, úC1ú, úC2ú, úC3ú по формулам (4.27) – (4.30). Шаг 4. Вычислить a0, a1, a2 по формулам (4.31). Шаг 5. Вычислить величину погрешности D2 = Шаг 5. Вывести на экран результаты : аппроксимирующую квадратичную функцию P2(x) = a0 + a1x + a2x2 и величину погрешности D2. Пример 4.6. Построим по методу наименьших квадратов многочлены первой и второй степени и оценим степень приближения. Значения yi в точках xi , i =0, 1, 2, 3, 4 приведены в таблице 2.3. Таблица 4.1
Вычислим коэффициенты c0, c1, c2, c3, c4, b0, b1, b2, по формулам (4.25), (4.26): c0 = 5; c1 = 15; c2 = 55; c3 = 225; c4 = 979; b0 = 12; b1 = 53; b2 = 235. 1. Линейная аппроксимация (m =1). 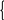 Система уравнений для определения коэффициентов a0 и a1 многочлена первой степени P2(x) = a0 + a1x + a2x2 имеет вид Система уравнений для определения коэффициентов a0 и a1 многочлена первой степени P2(x) = a0 + a1x + a2x2 имеет вид5a0 + 15a1 = 12 15a0 + 55a1 = 53 По формулам (4.23) найдем коэффициенты a0 и a1: a0 = P1(x) = a0 + a1x = –2.7 + 1.7x. 2. Квадратичная аппроксимация (m =2). Система уравнений для определения коэффициентов a0, a1 и a2 многочлена второй степени P2(x) = a0 + a1x + a2x2 имеет вид 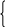 5a0 + 15a1 + 55a2 = 12 5a0 + 15a1 + 55a2 = 1215a0 + 55a1 + 225a2 = 53 55a0 + 225a1 + 979a2 = 235 По формулам (4.31) найдем коэффициенты a0, a1 и a2: a0 » –2.20, a1 » 1.27, a2 » 0.07. P2(x) = a0 + a1x + a2x2 = –2.20 + 1.27x + 0.07x2. Сравним значения, рассчитанные для функциональной зависимости, с исходными данными. Результаты приведены в табл.2.4. Таблица 4.2
Погрешность приближения в соответствии с формулами (4.24) и (4.32) составит D1 = D2 = |
