Вычислительная математика. Вычислительная_матиматика. Решение задач вычислительными методами. Основные понятия Погрешность

• Название: Решение задач вычислительными методами. Основные понятия Погрешность
• Анкор: Вычислительная математика
• Дата: 02.05.2021
• Размер: 1.45 Mb.
• Имя файла: Вычислительная_матиматика.doc
• Тип: Решение; #200900
• страница: 9 из 10

Указания к выполнению лабораторных работ

Программой курса предусмотрено проведение четырех лабораторных работ. Лабораторные работы ориентированы на использование системы Maple.

Система Maple V была создана группой символьных вычислений в 1980 году в университете Waterloo, Канада. В конце 1997 года вышла реализация Maple V R5.

Maple V принадлежит к классу прикладных программных пакетов, объединенных под общим названием Computer Algebra Systems (CAS) - системы компьютерной алгебры. Самым важным отличием Maple от таких пакетов как MathCad, MatLAB, Mathematica, является то, что она была изначально задумана как символьный пакет. Как и любой представитель данного семейства продуктов, Maple ориентирована на решение широкого ряда математических проблем. Она включает в себя большое количество специальных пакетов для решения задач линейной и тензорной алгебры, евклидовой и аналитической геометрии, теории чисел, теории графов, теории вероятностей, математической статистики, комбинаторики, теории групп, численной аппроксимации и линейной оптимизации, задач финансовой математики и многих других.

В основу Maple положен алгоритмический язык высокого уровня, предназначенный для реализации обычного процедурного программирования. Maple-язык "понимает" все стандартные объекты типа циклов (while, for), операторов условного перехода (if-then-else), массивов (array), списков (list), наборов (set), таблиц и т.д. Есть также возможность работы с файлами, что позволяет строить системы, состоящие из множества модулей, подгружая необходимые процедуры в процессе выполнения программы, а также реализовывать ввод и вывод больших объемов данных. Реализованы также все стандартные процедуры обработки строковой информации.

Применение Maple в образовании способствует повышению фундаментальности математического образования и сближает нашу образовательную систему с западной.

Лабораторные работы предполагают использование встроенных функций Maple, позволяющих решать основные задачи курса "Вычислительные методы".

В задачах используется параметр n – номер студента в списке группы.

Лабораторная работа №1.

Решение нелинейных уравнений и систем линейных уравнений.

Используемые функции: solve, fsolve, plot.

1. Найти точное решение уравнения:5x²+2x – n = 0.

2. Найти приближенное решение этого же уравнения.

3. Построить график левой части уравнения.

4. Найти приближенное решение уравнения x²e^x – n = 0.

5. Построить график левой части уравнения.

6. Найти точное решение системы уравнений.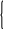

2x₁ + 6x₂ – x₃ = –12 + n

5x₁ – x₂ + 2x₃ = 29 + n

–3x₁ – 4x₂ + x₃ = 5 + n

7. Найти приближенное решение этой же системы уравнений.

Лабораторная работа №2.

Построение интерполяционных многочленов.

Используемые функции: interp, plot, subs.

1. Найти приближение функции, заданной в точках, многочленом, значения которого совпадают со значениями функции в указанных точках.

x 1 3 5 7 9

y 0+n 4+n 2+n 6+n 8+n

2. Построить график полученного интерполяционного многочлена .

3. Найти значение функции в точке x = 6.

Лабораторная работа №3.

Вычисление определенных интегралов.

Используемые функции: int, plot, evalf.

1. Найти аналитическое выражение для неопределенного интеграла .
2. Построить графики найденного интеграла - красным цветом и подинтегральной функции - синим цветом.

3. Вычислить значение этого интеграла в пределах от 2 до n + 2:

4. Вычислить приближенное значение интеграла .

Лабораторная работа №4.

Решение обыкновенных дифференциальных уравнений.

Используемыефункции: dsolve, plot, odeplot, op, with.

1. Найти аналитическое решение задачи Коши: y'(t) = (1/n)(t + y), y(0) = n.

2. Построить график найденного решения на отрезке [0, n].

3. Найти численное решение задачи Коши y'(t) = sin(ny(t))+t²), y(0) = n в точках t = 1 и t = 2.

4. Построить график найденного решений на отрезке [0, 5].

Указания к выполнению курсовых работ

Цель курсовой работы – приобретение студентами практического опыта реализации на ЭВМ алгоритмов численных методов для конкретных задач. Язык программирования выбирает студент.

Требования к выполнению курсовой работы

Результаты курсовой работы оформляются в виде отчета. Отчет по курсовой работе должен содержать следующие разделы:

1. Постановка задачи.

2. Описание математического метода.

3. Описание алгоритма реализации математического метода в виде блок-схемы или по шагам.

4. Листинг программы.

5. Контрольный пример. Анализ полученных результатов.