Вычислительная математика. Вычислительная_матиматика. Решение задач вычислительными методами. Основные понятия Погрешность

• Название: Решение задач вычислительными методами. Основные понятия Погрешность
• Анкор: Вычислительная математика
• Дата: 02.05.2021
• Размер: 1.45 Mb.
• Имя файла: Вычислительная_матиматика.doc
• Тип: Решение; #200900
• страница: 4 из 10

Обратный ход. Из последнего уравнения системы (3.13) находим x₄= 1.000. Подставляя значение x₄ в третье уравнение, получим x₃= 2.000. Подставляя найденные значения x₄и x₃ во второе уравнение, найдем x₂ = 3.000. Наконец, из первого уравнения, подставив в него найденные значения x₄, x₃и x₂, вычислим x₁= –1.000.

Итак система (3.10) имеет следующее решение:

x₁= 1.000, x₂ = 2.000, x₃= 3.000, x₄= – 1.000.

3.3. Метод исключения Гаусса с выбором главного элемента по столбцу

Хотя метод Гаусса является точным методом, ошибки округления могут привести к существенным погрешностям результата. Кроме того исключение по формулам (3.7) нельзя проводить, если элемент главной диагонали a равен нулю. Если элемент a мал, то велики ошибки округления при делении на этот элемент. Для уменьшения ошибок округления применяют метод исключения Гаусса с выбором главного элемента по столбцу. Прямой ход так же, как и для схемы единственного деления, состоит из n – 1 шагов. На первом шаге прежде, чем исключать переменную x₁, уравнения переставляются так, чтобы в левом верхнем углу был наибольший по модулю коэффициент a_i1, i = 1, 2, …, n. В дальнейшем, на k-м шаге, прежде, чем исключать переменную x_k, уравнения переставляются так, чтобы в левом верхнем углу был наибольший по модулю коэффициент a_ik, i = k, k + 1, …, n. После этой перестановки исключение переменной x_k производят, как в схеме единственного деления.

Трудоемкость метода. Дополнительные действия по выбору главных элементов требуют примерно n² операций, что практически не влияет на общую трудоемкость метода.

Пример 3.2.

Применим метод исключения Гаусса с выбором главного элемента по столбцу для решения системы уравнений (3.10) из примера 3.1. Прямой ход. 1-ый шаг. Так как коэффициент a₁₁ = 2.0 наибольший из коэффициентов первого столбца, перестановки строк не требуется и 1-ый шаг полностью совпадает с 1-ым шагом примера 3.1. Из второго, третьего и четвертого уравнений исключается переменная x₁ и система приводится к виду (3.11).

2-ой шаг. Наибольший по модулю коэффициент при x₂ в системе (3.11) a 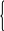= –1.15. Поэтому переставим уравнения следующим образом:

2.0x₁ + 1.0x₂– 0.1x₃ + 1.0x₄= 2.7

–1.15x₂ + 1.015x₃ + 5.05x₄= –4.305 (3.14)

0.3x₂ + 4.02x₃– 8.70x₄= 21.36

– 0.30x₂ + 2.55x₃–1.50x₄= 8.55

Вычислим множители:

m = = = –0.26087 m = = = 0.26087.

Вычитая из третьего и четвертого уравнений системы (3.14) второе уравнение, умноженное соответственно на m 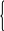и m , приходим к системе:

2.0x₁ + 1.0x₂– 0.1x₃ + 1.0x₄= 2.7

–1.15x₂ + 1.015x₃ + 5.05x₄= –4.305 (3.15)

4.28478x₃– 7.38261x₄= 20.23696

2.28522x₃– 2.81739x₄= 9.67305

3-ий шаг. Вычислим множитель:

m = = = 0.53333.

Вычитая из четвертого уравнения системы (3.15) третье, умноженное на m 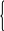, приведем систему к треугольному виду:

2.0x₁ + 1.0x₂– 0.1x₃ + 1.0x₄= 2.7

–1.15x₂ + 1.015x₃ + 5.05x₄= –4.305 (3.16)

4.28478x₃– 7.38261x₄= 20.23696

1.11998x₄= –1.11998

Обратный ход. Обратный ход полностью совпадает с обратным ходом примера 3.1. Решение системы имеет вид:

x₁= 1.000, x₂ = 2.000, x₃= 3.000, x₄= – 1.000.

3.4. Вычисление определителя методом исключения Гаусса

Из курса линейной алгебры известно, что определитель треугольной матрицы равен произведению диагональных элементов. В результате метода исключений Гаусса система линейных уравнений (3.2) с квадратной матрицей A приводится к эквивалентной ей системе (3.8) с треугольной матрицей A_n. Поэтому

det A = (–1)^s det A_n,

где s – число перестановок строк, (s = 0, если использовался метод Гаусса по схеме единственного деления).Таким образом,

det A = (–1)^s a₁₁ a a …a . (3.17)

Итак, для вычисления определителя det A необходимо выполнить процедуру прямого хода в методе Гаусса для системы уравнений Ax = 0, затем найти произведение главных элементов, стоящих на диагонали треугольной матрицы и умножить это произведение на (–1)^s, где s – число перестановок строк.

Пример 3.3.

Вычислим определитель det A =

2 .0 1.0 0.1 1.0

0.4 0.5 4.0 8.5

0.3 1.0 1.0 5.2

1.0 0.2 2.5 1.0

Данный определитель совпадает с определителем системы, рассмотренной в примере 3.1. Он равен произведению диагональных элементов треугольной матрицы (3.13):

det A = 2.0  0.30  16.425  1.12 = 11.0376.

Если же обратиться к примеру 3.2, то, учитывая, что была одна перестановка строк, т.е. s = 1, получим:

det A = (–1)  2.0  (–1.15)  4.28478  1.11998 = 11.0375.

3.5. Вычисление обратной матрицы методом исключения Гаусса

Обратной матрицей к матрице A называется матрица A^-1, для которой выполнено соотношение:

A A^-1 = E, (3.18)

г де E – единичная матрица:

1 0 0 … 0

0 1 0 … 0

E= 0 0 1 … 0 . (3.19)

…………….

0 0 0 … 1

Квадратная матрица A называется невырожденной, если det A  0. Всякая невырожденная матрица имеет обратную матрицу.

Вычисление обратной матрицы можно свести к рассмотренной выше задаче решения системы уравнений.

Пусть A – квадратная невырожденная матрица порядка n:

a₁₁ a₁₂ a₁₃ … a_1n

a₂₁ a₂₂ a₂₃ … a_2n

A = a₃₁ a₃₂ a₃₃ … a_3n

………………………

a_n1 a_n2 a_n3 … a_nn
и A^-1 – ее обратная матрица:

x₁₁ x₁₂ x₁₃ … x_1n

x₂₁ x₂₂ x₂₃ … x_2n

A^-1= x₃₁ x₃₂ x₃₃ … x_3n

………………………

x_n1 x_n2 x_n3 … x_nn

Используя соотношения (3.18), (3. 19) и правило умножения матриц, получим систему из n² уравнений с n² переменными x_ij, i, j = 1, 2, …, n. Чтобы получить первый столбец матрицы E, нужно почленно умножить каждую строку матрицы A на первый столбец матрицы A^-1 и приравнять полученное произведение соответствующему элементу первого столбца матрицы E. В результате получим систему уравнений:

a 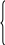₁₁x₁₁ + a₁₂x₂₁ + a₁₃x₃₁ + … + a_1nx_n1= 1

a₂₁x₁₁ + a₂₂x₂₁ + a₂₃x₃₁ + … + a_2nx_n1= 0

a₃₁x₁₁ + a₃₂x₂₁ + a₃₃x₃₁ + … + a_3nx_n1= 0(3.20)

……………………………………………….

a_n1x₁₁ + a_n2x₂₁ + a_n3x₃₁ + … + a_nnx_n1= 0

А налогично, чтобы получить второй столбец матрицы E, нужно почленно умножить каждую строку матрицы A на второй столбец матрицы A^-1 и приравнять полученное произведение соответствующему элементу второго столбца матрицы E. В результате получим систему уравнений:

a₁₁x₁₂ + a₁₂x₂₂ + a₁₃x₃₂ + … + a_1nx_n2= 0

a₂₁x₁₂ + a₂₂x₂₂ + a₂₃x₃₂ + … + a_2nx_n2= 1

a₃₁x₁₂ + a₃₂x₂₂ + a₃₃x₃₂ + … + a_3nx_n2= 0(3.21)

……………………………………………….

a_n1x₁₂ + a_n2x₂₂ + a_n3x₃₂ + … + a_nnx_n2= 0

и т. д.

Всего таким образом получим n систем по n уравнений в каждой системе, причем все эти системы имеют одну и ту же матрицу A и отличаются только свободными членами. Приведение матрицы A к треугольной по формулам (3.7) делается при этом только один раз. Затем по последней из формул (3.7) преобразуются все правые части, и для каждой правой части делается обратный ход.

Пример 3.4.

Вычислим обратную матрицу A^-1 для матрицы A =

1 .8 –3.8 0.7 –3.7

0.7 2.1 –2.6 –2.8

7.3 8.1 1.7 –4.9

1.9 –4.3 –4.3 –4.7

По формулам (3.7) за три шага прямого хода преобразуем матрицу A в треугольную матрицу

1 .8 –3.8 0.7 –3.7

0 3.57778 –2.87222 –1.36111

0 0 17.73577 19.04992

0 0 0 5.40155
Далее, применим процедуру обратного хода четыре раза для столбцов свободных членов, преобразованных по формулам (3.7) из столбцов единичной матрицы:




1 0 0 0

0 1 0 0

0 , 0 , 1 , 0 .

0 0 0 1

Каждый раз будем получать столбцы матрицы A^-1. Опустив промежуточные вычисления, приведем окончательный вид матрицы A^-1:

– 0.21121 –0.46003 0.16248 0.26956

–0.03533 0.16873 0.01573 –0.08920

0.23030 0.04607 –0.00944 –0.19885 .

–0.29316 –0.38837 0.06128 0.18513

3.6. Метод простой итерации Якоби

Метод Гаусса обладает довольно сложной вычислительной схемой. Кроме того, при вычислениях накапливается ошибка округления, что может привести к недостаточно точному результату. Рассмотрим метод простой итерации Якоби, свободный от этих недостатков, хотя требующий приведения исходной системы уравнений к специальному виду.

Для того, чтобы применить метод простой итерации, необходимо систему уравнений

Ax = b (3.22)

с квадратной невырожденной матрицей A привести к виду

x = Bx + c, (3.23)

где B – квадратная невырожденная матрица с элементами b_ij, i, j = 1, 2, …, n, x – вектор-столбец неизвестных x_i, c – вектор-столбец с элементами c_i, i = 1, 2, …, n.

Существуют различные способы приведения системы (3.22) к виду (3.23). Рассмотрим самый простой. Представим систему (3.22) в развернутом виде:

a ₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ + … + a_2nx_n = b₂

a₃₁x₁ + a₃₂x₂ + a₃₃x₃ + … + a_3nx_n = b₃(3.24)

…………………………………………….

a_n1x₁ + a_n2x₂ + a_n3x₃ + … + a_nnx_n = b_n

Из первого уравнения системы (3.24) выразим неизвестную x₁:

x₁ = a (b₁ – a₁₂x₂ – a₁₃x₃ – … – a_1nx_n),

из второго уравнения – неизвестную x₂:

x₂ = a (b₂ – a₂₁x₁ – a₂₃x₃ – … – a_2nx_n),

и т. д. В результате получим систему:

x ₁= b₁₂x₂ + b₁₃x₃ + … + b_1,n-1x_n-1 + b_1nx_n + c₁

x₂= b₂₁x₁+ b₂₃x₃ + … + b_2,n-1x_n-1+ b_2nx_n + c₂

x₃= b₃₁x₁ + b₃₂x₂+ … + b_3,n-1x_n-1+b_3nx_n + c₃(3.25)

…………………………………………………………………..

x_n= b_n1x₁ + b_n2x₂ + b_n3x₃ + b_n,n-1x_n-1+ c_n

Матричная запись системы (3.25) имеет вид (3.23). На главной диагонали матрицы B находятся нулевые элементы, а остальные элементы вычисляются по формулам:

b_ij = , c_i = , i, j = 1,2, …n, i j. (3.26)

Очевидно, что диагональные элементы матрицы A должны быть отличны от нуля.

В ыберем произвольно начальное приближение Обычно в качестве первого приближения берут x = c_i или x = 0. Подставим начальное приближение в правую часть (3.25). Вычисляя левые части, получим значения x , x , …, x . Продолжая этот процесс дальше, получим последовательность приближений, причем (k + 1)-е приближение строится следующим образом:

x = b₁₂x + b₁₃ x + … + b_1,n-1 x + b_1n x + c₁

x = b₂₁x ₁+ b₂₃ x + … + b_2,n-1 x + b_2n x + c₂

x = b₃₁x + b₃₂ x + … + b_3,n-1 x +b_3n x + c₃ … (3.27)

x = b_n1x + b_n2x + b_n3 x + b_n,n-1 x + c._n

Система (3.27) представляет собой расчетные формулы метода простой итерации Якоби.