Вычислительная математика. Вычислительная_матиматика. Решение задач вычислительными методами. Основные понятия Погрешность
 Скачать 1.45 Mb.
|
|
Тема 6. Численное решение дифференциальных уравнений 6.1. Постановка задачи Коши Известно, что обыкновенное дифференциальное уравнение первого порядка имеет вид: y' (t) = f(t, y(t)). (6.1) Решением уравнения (6.1) является дифференцируемая функция y(t), которая при подстановке в уравнение (6.1) обращает его в тождество. На рис. 6.1 приведен график решения дифференциального уравнения (6.1). График решения дифференциального уравнения называется интегральной кривой. 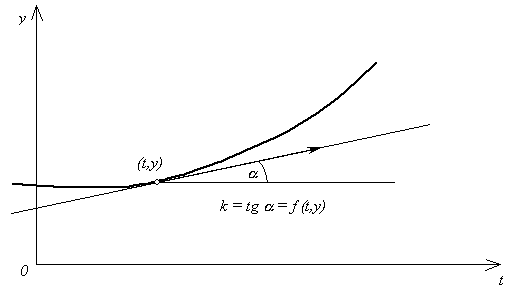 Рис. 6.1 Производную y'(t) в каждой точке (t, y) можно геометрически интерпретировать как тангенс угла наклона касательной к графику решения, проходящего через эту точку, т е.: k = tg = f(t, y). Уравнение (6.1) определяет целое семейство решений. Чтобы выделить одно решение, задают начальное условие: y(t0 ) = y0, (6.2) где t0 – некоторое заданное значение аргумента t, а y0 – начальное значение функции. Задача Коши заключается в отыскании функции y = y(t), удовлетворяющей уравнению (6.1) и начальному условию (6.2). Обычно определяют решение задачи Коши на отрезке, расположенном справа от начального значения t0, т. е. для t [t0, T]. Разрешимость задачи Коши определяет следующая теорема. Теорема 6.1. Пусть функция f(t, y) определена и непрерывна при t0 t T, -< y < и удовлетворяет условию Липшица: | f(t, y1) – f(t, y2)| L| y1 – y2|, где L некоторая постоянная, а y1 , y2 – произвольные значения. Тогда для каждого начального значения y0 существует единственное решение y(t) задачи Коши для t [t0, T]. Даже для простых дифференциальных уравнений первого порядка не всегда удается получить аналитическое решение. Поэтому большое значение имеют численные методы решения. Численные методы позволяют определить приближенные значения искомого решения y(t) на некоторой выбранной сетке значений аргумента ti, (i = 0, 1, …). Точки ti называются узлами сетки, а величина hi = ti+1 – ti – шагом сетки. Часто рассматривают равномерные сетки, для которых шаг hiпостоянен, hi= h =  . При этом решение получается в виде таблицы, в которой каждому узлу сетки ti соответствуют приближенные значения функции y(t) в узлах сетки yi y(ti).Численные методы не позволяют найти решение в общем виде, зато они применимы к широкому классу дифференциальных уравнений. Сходимость численных методов решения задачи Коши. Пусть y(t) – решение задачи Коши. Назовем глобальной погрешностью (или просто погрешностью) численного метода функцию i = y(ti) – yi , заданную в узлах сетки ti. В качестве абсолютной погрешности примем величину R =  | y(ti) – yi|Численный метод решения задачи Коши называется сходящимся, если для него R 0 при h 0. Говорят, что метод имеет p-ый порядок точности, если для погрешности справедлива оценка R Chp, p > 0, C – константа, C 0. 6.2. Метод Эйлера Простейшим методом решения задачи Коши является метод Эйлера. Будем решать задачу Коши y' (t) = f(t, y(t)). y(t0 ) = y0, на отрезке [t0, T]. Выберем шаг h = , и построим сетку с системой узлов ti = t0 + ih, i = 0, 1, …, n. В методе Эйлера вычисляются приближенные значения функции y(t) в узлах сетки : yi y(ti). Заменив производную y' (t) конечными разностями на отрезках [ti, ti+1], i = 0, 1, …, n – 1, получим приближенное равенство:  = f(ti, yi), i = 0, 1, …, n – 1, которое можно переписать так: yi+1 = yi + h f(ti, yi), i = 0, 1, …, n – 1. (6.3) Формулы (6.3) и начальное условие (6.2) являются расчетными формулами метода Эйлера. Геометрическая интерпретация одного шага метода Эйлера заключается в том, что решение на отрезке [ti, ti+1] заменяется касательной y = y' (ti)( t - ti), проведенной в точке (ti, y(ti)) к интегральной кривой, проходящей через эту точку. После выполнения n шагов неизвестная интегральная кривая заменяется ломаной линией (ломаной Эйлера). Оценка погрешности. Для оценки погрешности метода Эйлера воспользуемся следующей теоремой. Теорема 6.2. Пусть функция f удовлетворяет условиям:  K,  =  L. (6.4)Тогда для метода Эйлера справедлива следующая оценка погрешности: R =  | y(ti) – yi|  =  ,где l – длина отрезка [t0, T]. Мы видим , что метод Эйлера имеет первый порядок точности. Оценка погрешности метода Эйлера часто бывает затруднительна, так как требует вычисления производных функции f(t, y(t)). Грубую оценку погрешности дает правило Рунге (правило двойного пересчета), которое используется для различных одношаговых методов, имеющих p-ый порядок точности. Правило Рунге заключается в следующем. Пусть y  – приближения, полученные с шагом  , а y – приближения, полученные с шагом h. Тогда справедливо приближенное равенство:|y - y(ti)|  |y - y | . (6.5)Таким образом, чтобы оценить погрешность одношагового метода с шагом , нужно найти то же решение с шагом h и вычислить величину, стоящую справа в формуле (6.5), т е.R |y - y | (6.6)Так как метод Эйлера имеет первый порядок точности, т. е. p = 1, то приближенное равенство (6.6) примет вид R |y - y | (6.7)Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши с заданной точностью . Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение y , i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:R |y - y | < . (6.8)Для метода Эйлера условие (6.8) примет вид R |y - y | < (6.9)Приближенным решением будут значения y , i = 0, 1, …, n.Пример 6.1. Найдем решение на отрезке [0, 1] следующей задачи Коши: y' (t) = y –  , (6.10)y(0) = 1. Возьмем шаг h = 0.2. Тогда n =  = 5.В соответствии с (6.3) получим расчетную формулу метода Эйлера: yi+1 = yi + 0.2  , y0 = 1, i = 0, 1, 2, 3, 4, 5.Решение представим в виде таблицы 6.1: Таблица 6.1
Уравнение (6.10) есть уравнение Бернулли. Его решение можно найти в явном виде: y =  . (6.11)Для сравнения точного и приближенного решений представим точное решение (6.11) в виде таблицы 6.2: Таблица 6.2
Из таблицы видно, что погрешность составляет R =  | y(ti) – yi| = 0.0917.6.3. Модифицированные методы Эйлера Первый модифицированный метод Эйлера. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения искомой функции y  в точках t = ti + с помощью формулы:y = yi + fi = yi + f(ti, yi).Затем находится значение правой части уравнения (6.1) в средней точке f = f(t , y )и затем полагается yi+1 = yi + h f , i = 0, 1, …, n – 1. (6.12)Формулы (6.12) являются расчетными формулами первого модифицированного метода Эйлера. Первый модифицированный метод Эйлера является одношаговым методом со вторым порядком точности Второй модифицированный метод Эйлера – Коши. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения  = yi + h f(ti, yi). (6.13)Затем приближения искомого решения находятся по формуле: yi+1 = yi + [f(ti, yi) + f(ti+1, )], i = 0, 1, …, n – 1. (6.14)Формулы (6.14) являются расчетными формулами второго модифицированного метода Эйлера – Коши. Второй модифицированный метод Эйлера – Коши, так же, как и первый, является одношаговым методом со вторым порядком точности. Оценка погрешности. Приближенная оценка погрешности модифицированных методов Эйлера осуществляется как и для простого метода Эйлера с использованием правила Рунге (см. предыдущий раздел 6.2). Так как оба модифицированных метода Эйлера имеют второй порядок точности, т. е. p = 2, то оценка погрешности (6.6) примет вид R  |y - y |. (6.15)Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши модифицированными методами Эйлера с заданной точностью . Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение y , i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:R |y - y | < . (6.16)Приближенным решением будут значения y , i = 0, 1, …, n.Пример 6.2. Применим первый модифицированный метод Эйлера для решения задачи Коши y' (t) = y – , y(0) = 1,рассмотренной ранее в примере 6.1. Возьмем шаг h = 0.2. Тогда n = = 5.В соответствии с (6.3) получим расчетную формулу первого модифицированного метода Эйлера: yi+1 = yi + h f = yi + 0.2 f , где f = f(t , y ) = y –  ,t = ti + = ti + 0.1,y = yi + f(ti, yi) = yi +0.1 ,t0 = 0, y0 = 1, i = 0, 1, …, 4. Решение представим в виде таблицы 6.3: Таблица 6.3
Третий столбец таблицы 6.3 содержит приближенное решение yi, i = 0, 1, …, 5. Сравним полученное приближенное решение с точным решением (6.11), представленном в таблице 6.2. Виднм, что погрешность составляет R = | y(ti) – yi| = 0.0042.Пример 6.3. Применим второй модифицированный метод Эйлера – Коши для решения задачи Коши y' (t) = y – , y(0) = 1,рассмотренной ранее в примерах 6.1 и 6.2. Так же, как и ранее, зададим шаг h = 0.2. Тогда n = = 5.В соответствии с (6.14) получим расчетную формулу метода Эйлера – Коши: yi+1 = yi + [f(ti, yi) + f(ti+1, )] = yi + 0.1[f(ti, yi) + f(ti+1, )], где f(ti, yi) = yi –  = yi + h f(ti, yi) = yi + 0.1 t0 = 0, y0 = 1, i = 0, 1, …, 4. Решение представим в виде таблицы 6.4: Таблица 6.4
Таблица 6.4 заполняется последовательно по строкам, сначала первая строка, затем вторая и т. д. Третий столбец таблицы 6.4 содержит приближенное решение yi, i = 0, 1, …, 5. Сравним полученное приближенное решение с точным решением (6.11), представленном в таблице 6.2. Видим, что погрешность составляет R = | y(ti) – yi| = 0.0222.6.4. Метод Рунге – Кутта Метод Рунге – Кутта является одним из наиболее употребительных методов высокой точности. Метод Эйлера можно рассматривать как простейший вариант метода Рунге – Кутта. Рассмотрим задачу Коши для дифференциального уравнения y' (t) = f(t, y(t)) с начальным условием y(t0 ) = y0. Как и в методе Эйлера, выберем шаг h = и построим сетку с системой узлов ti = t0 + ih, i = 0, 1, …, n. Обозначим через yi приближенное значение искомого решения в точке ti. Приведем расчетные формулы метода Рунге – Кутта четвертого порядка точности: yi+1 = yi +  h(k + 2k + 2k + k ),k = f(ti, yi),k = f(ti + , yi + k ), (6.17)k = f(ti + , yi + k ),k = f(ti +h, yi + hk ),i = 0, 1, …, n. Оценка погрешности. Оценка погрешности метода Рунге – Кутта затруднительна. Грубую оценку погрешности дает правило Рунге (см. раздел 6.2). Так как метод Рунге - Кутта имеет четвертый порядок точности, т. е. p = 4, то оценка погрешности (6.6) примет вид R  |y - y |. (6.18)Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши методом Рунге – Кутта четвертого порядка точности с заданной точностью . Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение y , i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:R |y - y | < . (6.19)Приближенным решением будут значения y , i = 0, 1, …, n.Пример 6.4. Методом Рунге – Кутта четвертого порядка точности найдем решение на отрезке [0, 1] следующей задачи Коши. y' (t) = 2ty, y(0) = 1. (6.20) Возьмем шаг h = 0.1. Тогда n =  = 10.В соответствии с (6.17) расчетные формулы примут вид: yi+1 = yi + h(k + 2k + 2k + k ),k = 2tiyi,k = 2(ti + )(yi + k ), (6.21)k = 2(ti + )(yi + k ),k = 2(ti +h)(yi + hk ),i = 0, 1, …, 10. Задача (6.20) имеет точное решение: y(t) = e  , поэтому погрешность определяется как абсолютная величина разности между точными и приближенными значениями i = | y(ti) – yi|. Найденные по формулам (6.21) приближенные значения решения yi и их погрешности i представлены в таблице 6.5: Таблица 6.5
Задачи к зачету по курсу “Вычислительные методы”Указание. Каждый студент вначале должен определить параметр своего контрольного задания, s = log10(1 +  ), где k - номер студента в списке группы, k = 1, 2, … Решение задач должно быть оформлено аккуратно и содержать все промежуточные расчеты. В качестве образца можно взять примеры, рассмотренные в соответствующих разделах методических указаний. 1. Методом деления отрезка пополам найти корень уравнения 4(1 – x2) – ex= s с точностью = 10-3. 2. Методом Зейделя решить систему уравнений с точностью =10-3.   6.2+s 2.2+s 1.2+s 16.55+sA = 2.2+s 5.5+s -1.5+s , b = 10.55+s . 1.2+s -1.5+s 7.2 +s 16.80+s 3. Найти приближение функции f(x) = esx на отрезке [0, 1] многочленом Тейлора с точностью = 10-3 . Вычислить es. 4. Вычислить приближенно по формуле средних прямоугольников интеграл  при n = 4 и оценить погрешность результата.5. Методом Эйлера найти численное решение задачи Коши y'= 2sy; y(0) = 1, на отрезке [0, 1] с шагом h = 0.2. Сравнить с точным решением. |