Вычислительная математика. Вычислительная_матиматика. Решение задач вычислительными методами. Основные понятия Погрешность

• Название: Решение задач вычислительными методами. Основные понятия Погрешность
• Анкор: Вычислительная математика
• Дата: 02.05.2021
• Размер: 1.45 Mb.
• Имя файла: Вычислительная_матиматика.doc
• Тип: Решение; #200900
• страница: 7 из 10

Тема 5. Численное интегрирование функций одной переменной

5.1. Постановка задачи численного интегрирования

Далеко не все интегралы можно вычислить по известной из математического анализа формуле Ньютона – Лейбница:

I = = F(b) – F(a), (5.1)

где F(x) – первообразная функции f(x). Например, в элементарных функциях не выражается интеграл . Но даже в тех случаях, когда удается выразить первообразную функцию F(x) через элементарные функции, она может оказаться очень сложной для вычислений. Кроме того, точное значение интеграла по формуле (5.1) нельзя получить, если функция f(x) задается таблицей. В этих случаях обращаются к методам численного интегрирования.

Суть численного интегрирования заключается в том, что подынтегральную функцию f(x) заменяют другой приближенной функцией, так, чтобы, во-первых, она была близка к f(x) и, во вторых, интеграл от нее легко вычислялся. Например, можно заменить подынтегральную функцию интерполяционным многочленом. Широко используют квадратурные формулы:

 , (5.2)

где x_i – некоторые точки на отрезке [a, b],называемые узлами квадратурной формулы, A_i– числовые коэффициенты, называемые весами квадратурной формулы, n 0 – целое число.

5.2. Метод прямоугольников

Формулу прямоугольников можно получить из геометрической интерпретации интеграла. Будем интерпретировать интеграл 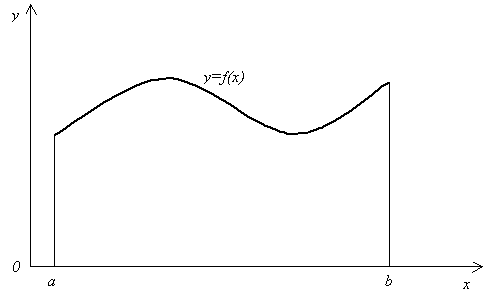как площадь криволинейной трапеции, ограниченной графиком функции y = f(x), осью абсцисс и прямыми x = a и x = b (рис. 5.1).



Рис. 5.1

Разобьем отрезок [a, b] на n равных частей длиной h, так, что h = 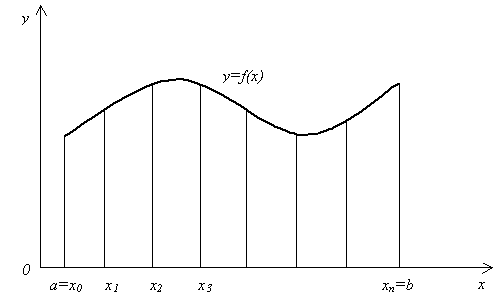. При этом получим точки a = x₀< x₁< x₂ < … < x_n = b и x_i+1= x_i + h, i = 0, 1, … , n – 1 (рис. 5.2)



Рис. 5.2

Заменим приближенно площадь криволинейной трапеции площадью ступенчатой фигуры, изображенной на рис. 5.3.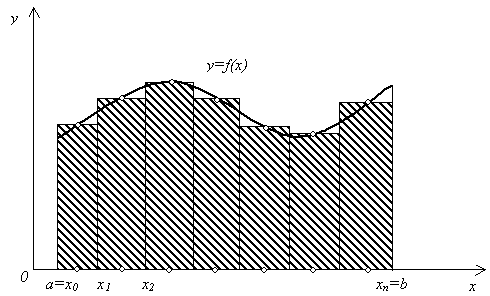



Рис. 5.3

Эта фигура состоит из n прямоугольников. Основание i-го прямоугольника образует отрезок [x_i, x_i+1] длины h, а высота основания равна значению функции в середине отрезка [x_i, x_i+1], т е. f 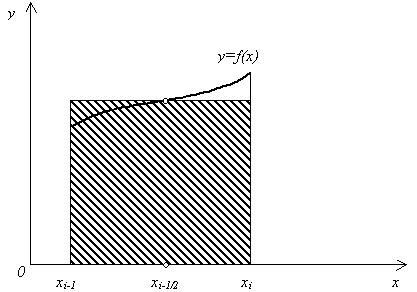(рис. 5.4).


Рис. 5.4

Тогда получим квадратурную формулу средних прямоугольников:

I =  I_пр = (5.3)

Формулу (5.3) называют также формулой средних прямоугольников. Иногда используют формулы

I  I = , (5.4)

I  I = , (5.5)

которые называют соответственно квадратурными формулами левых и правых прямоугольников.

Геометрические иллюстрации этих формул приведены на рис. 5.5 и 5.6.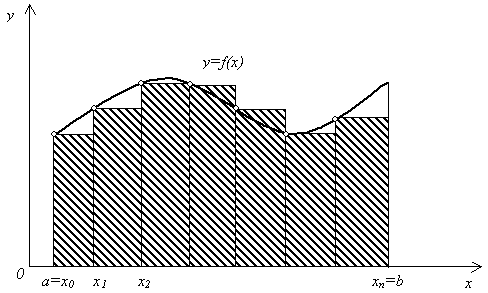



Рис. 5.5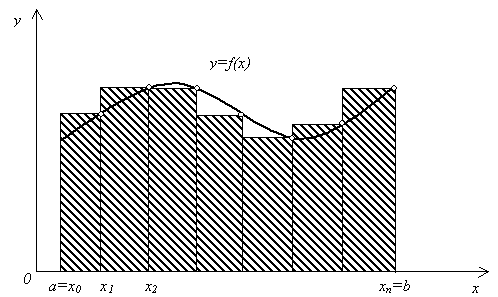



Рис. 5. 6

Оценка погрешности. Для оценки погрешности формулы прямоугольников воспользуемся следующей теоремой .

Теорема 5.1. Пусть функция f дважды непрерывно дифференцируема на отрезке [a, b]. Тогда для формулы прямоугольников справедлива следующая оценка погрешности:

| I – I_пр |  h², (5.6)

где M₂ = |f "(x)|

Пример 5.1.

Вычислим значение интеграла по формуле средних прямоугольников (5.3) с шагом h = 0.1.

Составим таблицу значений функции e (табл. 5.1):

Таблица 5.1

x	e	x	e
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50	1.0000000 0.9975031 0.9900498 0.9777512 0.9607894 0.9394131 0.9139312 0.8847059 0.8521438 0.8166865 0.7788008	0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00	0.7389685 0.6976763 0.6554063 0.6126264 0.5697828 0.5272924 0.4855369 0.4448581 0.4055545 0.3678794

Производя вычисления по формуле (5.3), получим:

I_пр = 0.74713088.

Оценим погрешность полученного значения. Имеем:

f "(x) = (e )" = (4x² – 2) e . Нетрудно убедиться, что | f "(x)|  M₂ = 2. Поэтому по формуле(5.4)

| I – I_пр |  (0.1)²  0.84 10^-3.

5.3. Метод трапеций

Выведем формулу трапеций так же, как и формулу прямоугольников, из геометрических соображений. Заменим график функции y = f(x) (рис.5.1) ломаной линией (рис.5.7), полученной следующим образом. Из точек a = x₀, x₁, x₂,…, x_n = b проведем ординаты до пересечения с кривой y = f(x). Концы ординат соединим прямолинейными отрезками.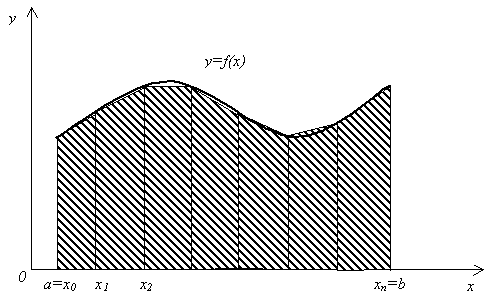



Рис. 5.7

Тогда площадь криволинейной трапеции приближенно можно считать равной площади фигуры, составленной из трапеций. Так как площадь трапеции, построенной на отрезке [x_i, x_i+1] длины h 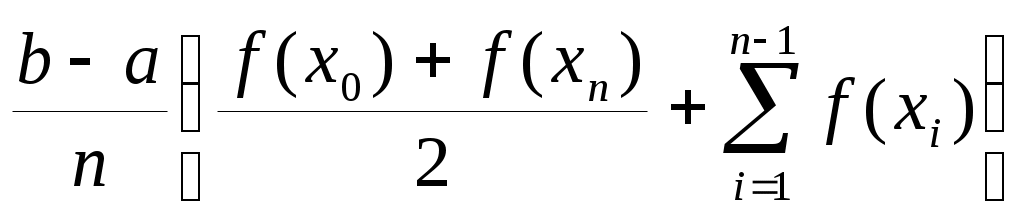= , равна h , то, пользуясь этой формулой для i = 0, 2, … , n – 1, получим квадратурную формулу трапеций:

I= I_тр =h = (5.7)

Оценка погрешности. Для оценки погрешности формулы трапеций воспользуемся следующей теоремой.

Теорема 5.2. Пусть функция f дважды непрерывно дифференцируема на отрезке [a, b]. Тогда для формулы трапеций справедлива следующая оценка погрешности:

| I – I_тр |  h², (5.8)

где M₂ = |f "(x)|.

Пример 5.2.

Вычислим значение интеграла по формуле трапеций (5.7) и сравним полученный результат с результатом примера 5.1.

Используя таблицу значений функции e из примера 5.1 и производя вычисления по формуле трапеций (5.7), получим:

I_тр = 0.74621079.

Оценим погрешность полученного значения. В примере (5.1) получили оценку: | f "(x)|  M₂ = 2. Поэтому по формуле (5.8)

| I – I_тр |  (0.1)²  1.7 10^-3.

Сравнивая результаты примеров 5.1 и 5.2, видим, что метод средних прямоугольников имеет меньшую погрешность, т.е. он более точный.

5.4. Метод Симпсона (метод парабол)

Заменим график функции y = f(x) на отрезке [x_i, x_i+1], i = 0, 2, … , n – 1, параболой, проведенной через точки (x_i, f(x_i)), (x ,f(x )), (x_i+1, f(x_i+1)), где x - середина отрезка [x_i, x_i+1]. Эта парабола есть интерполяционный многочлен второй степени L₂(x) с узлами x_i, x , x_i+1. Нетрудно убедиться, что уравнение этой параболы имеет вид:

y = L₂(x) =

f(x ) + (x – x ) + (x - x )², (5.9)

где h = .

Проинтегрировав функцию (5.9) на отрезке [x_i, x_i+1], получим

I_i = 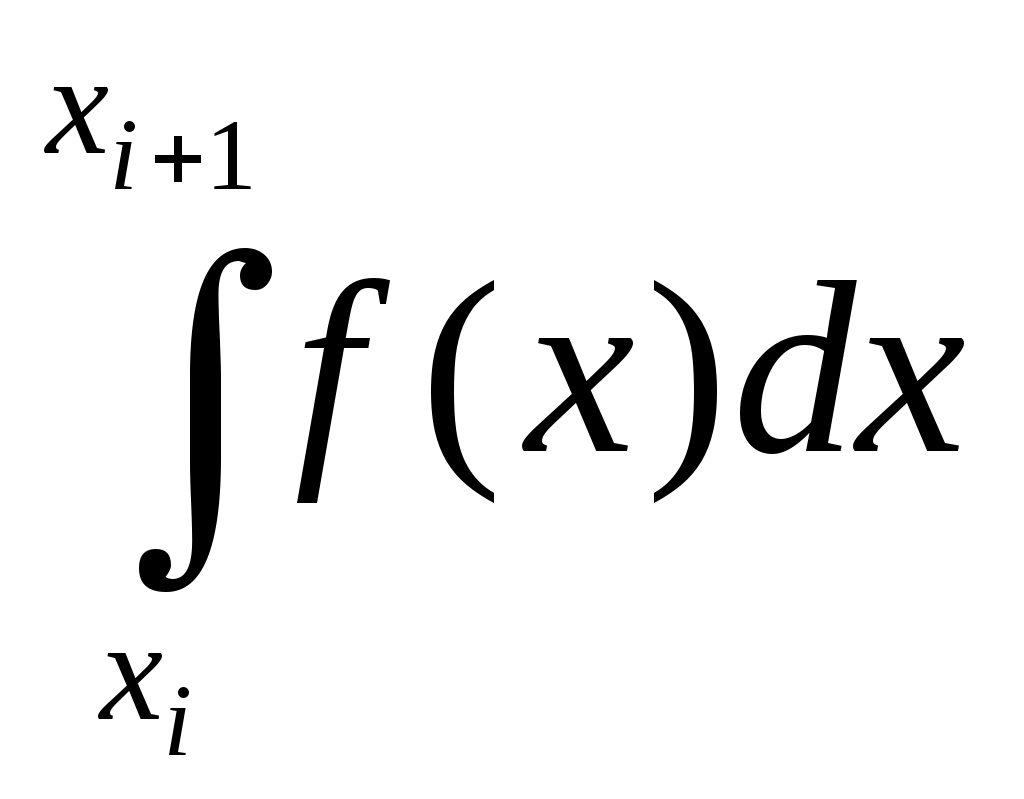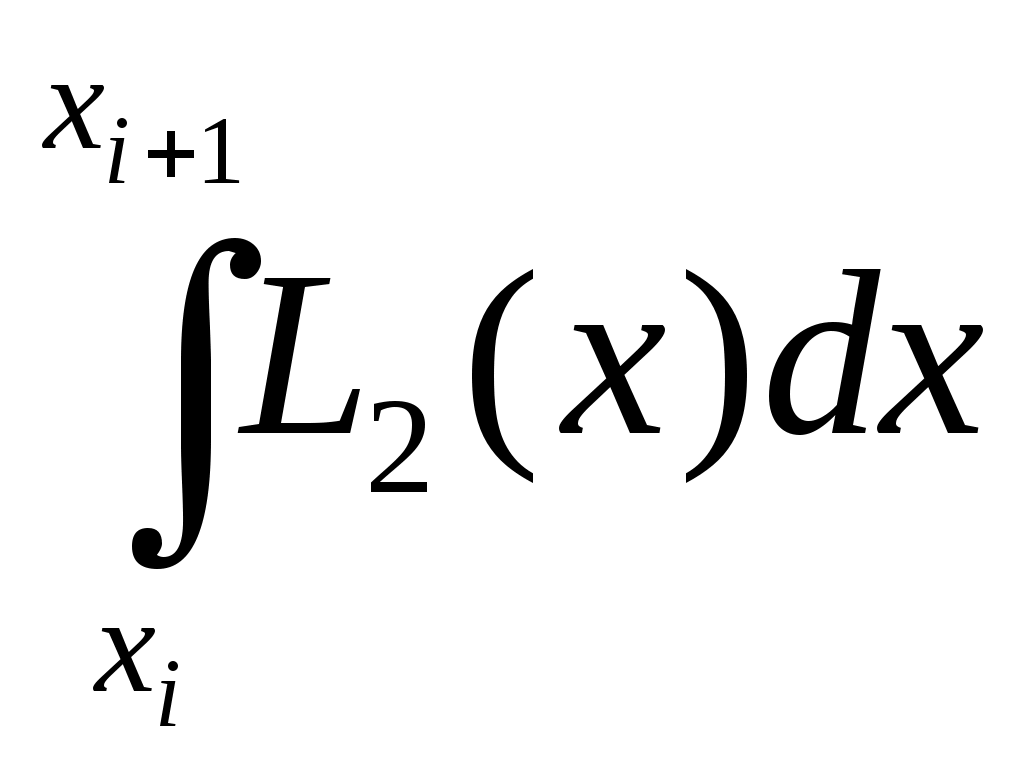 = ( f(x_i) + 4f(x ) + f(x_i+1)). (5.10)

Суммируя выражение (5.10) по i = 0, 1, 2, … , n – 1, получим квадратурную формулу Симпсона (или формулу парабол):

I =  I_С = ( f(x₀) + f(x_n) + 4 + 2 ). (5.11)

Оценка погрешности. Для оценки погрешности формулы Симпсона воспользуемся следующей теоремой.

Теорема 5.2. Пусть функция f имеет на отрезке [a, b] непрерывную производную четвертого порядка f ⁽⁴⁾(x). Тогда для формулы Симпсона (5.9) справедлива следующая оценка погрешности:

| I – I_С |  h⁴, (5.12)

где M₄ = | f ⁽⁴⁾(x)|.

Замечание.Если число элементарных отрезков, на которые делится отрезок [a, b], четно , т.е. n = 2m, то параболы можно проводить через узлы с целыми индексами, и вместо элементарного отрезка [x_i, x_i+1] длины h рассматривать отрезок [x_2i, x_2i+2] длины 2h. Тогда формула Симпсона примет вид:

I  (f(x₀) + f(x_2m) + 4 + 2 ), (5.13)

а вместо оценки (5.10) будет справедлива следующая оценка погрешности:

| I – I_С |  h⁴, (5.14)

Пример 5.3.

Вычислим значение интеграла по формуле Симпсона (5.11) и сравним полученный результат с результатами примеров 5.1 и 5.2.

Используя таблицу значений функции e из примера 5.1 и производя вычисления по формуле Симпсона (5.11) , получим:

I_С = 0.74682418.

Оценим погрешность полученного значения. Вычислим четвертую производную f ⁽⁴⁾(x).

f ⁽⁴⁾(x) = (16x⁴ – 48x² + 12) e , | f ⁽⁴⁾(x)|  12.

Поэтому

| I – I_С |  (0.1)⁴  0.42  10^-6.

Сравнивая результаты примеров 5.1, 5.2 и 5.3, видим , что метод Симпсона имеет меньшую погрешность, чем метод средних прямоугольников и метод трапеций.

5.5. Правило Рунге практической оценки погрешности

Оценки погрешности по формулам (5.4), (5.8) и (5.12) являются априорными. Они зависят от длины элементарного отрезка h, и при достаточно малом h справедливо приближенное равенство:

I – I^h  Ch^k, (5.15)

где I^h приближенное значение интеграла, вычисленное по одной из формул (5.3), (5.5), (5.9), C  0 и k > 0 – величины, не зависящие от h.

Если уменьшить шаг h в два раза, то, в соответствии с (5.15) получим:

I – I^h/2  Ch^k  ( I – I^h). (5.16)

Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f (x). В вычислительной практике используются другие оценки.

Вычтем из равенства (5.15) равенство (5.16):

I^h/2 – I^h  Ch^k(2^k – 1). (5.17)

Учитывая приближенное равенство (5.16), получим следующее приближенное равенство:

I – I^h/2 . (5.18)

Приближенное равенство (5.18) дает апостериорную оценку погрешности. Вычисление этой оценки называется правилом Рунге. Правило Рунге – это эмпирический способ оценки погрешности, основанный на сравнении результатов вычислений , проводимых с разными шагами h.

Для формул прямоугольников и трапеций k = 2, а для формулы Симпсона k = 4. Поэтому для этих формул приближенное равенство (5.18) принимает вид:

I – I_пр  , (5.19)

I – I_тр  , (5.20)

I – I_С  . (5.21)

Используя правило Рунге, можно построить процедуру приближенного вычисления интеграла с заданной точностью . Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значения в два раза, каждый раз вычисляя приближенное значение I . Вычисления прекращаются тогда, когда результаты двух последующих вычислений будут различаться меньше, чем на .
Пример 5.4.

Найдем значение интеграла с точностью  = 10^-4, используя формулу трапеций и применяя вышеизложенную процедуру дробления шага. В примере 5.2 было получено значение I при h₁= 0.1, I^h =0.74621079. Уменьшим шаг вдвое: h₂ = 0.05 и вычислим I = 0.74667084, ₂ = ( I - I ) = (0.74667084 – 0.74621079)  1.510^-4. Так как |₂| > , то снова дробим шаг: h₃ = 0.025, вычисляем I = 0.74678581, ₂ = ( I - I ) = (0.74678581 – 0.74667084)  410^-5. Поскольку |₃| < , требуемая точность достигнута и I  0.7468  0.0001.