Вычислительная математика. Вычислительная_матиматика. Решение задач вычислительными методами. Основные понятия Погрешность
 Скачать 1.45 Mb.
|
Тема 2. Решение нелинейных уравнений2.1. Постановка задачи Пусть дана некоторая функция f(x) и требуется найти все или некоторые значения x, для которых f(x) = 0. (2.1) Значение x*, при котором f(x*) = 0, называется корнем (или решением) уравнения (2.1). Относительно функции f(x) часто предполагается, что f(x) дважды непрерывно дифференцируема в окрестности корня. Корень x* уравнения (2.1) называется простым, если первая производная функции f(x) в точке x* не равна нулю, т. е. f '(x*)  0. Если же f '(x*) = 0, то корень x* называется кратным корнем.Геометрически корень уравнения (2.1) есть точка пересечения графика функции y = f(x) с осью абсцисс. На рис. 2.1 изображен график функции y = f(x), имеющей четыре корня: два простых (x 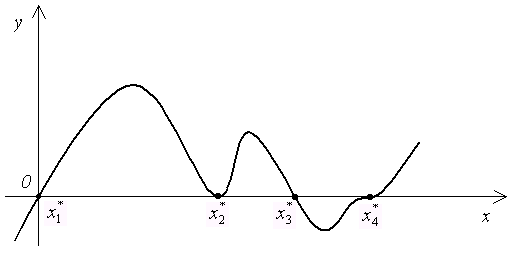 и x ) и два кратных (x и x ). Рис. 2.1. Большинство методов решения уравнения (2.1) ориентировано на отыскание простых корней уравнения (2.1). 2.2. Основные этапы отыскания решения В процессе приближенного отыскания корней уравнения (2.1) обычно выделяют два этапа: локализация (или отделение) корня и уточнение корня. Локализация корня заключается в определении отрезка [a, b], содержащего один и только один корень. Не существует универсального алгоритма локализации корня. В некоторых случаях отрезок локализации может быть найден из физических соображений. Иногда удобно бывает локализовать корень с помощью построения графика или таблицы значений функции y = f(x). На наличие корня на отрезке [a, b] указывает различие знаков функции на концах отрезка. Основанием для этого служит следующая теорема математического анализа. Теорема 2.1. Если функция f непрерывна на отрезке [a, b] и принимает на его концах значения разных знаков, так, что f(a)f(b) < 0, то отрезок [a, b] содержит по крайней мере один корень уравнения f(x) = 0. Однако, корень четной кратности таким образом локализовать нельзя, так как в окрестности такого корня функция f(x) имеет постоянный знак. На этапе уточнения корня вычисляют приближенное значение корня с заданной точностью > 0. Приближенное значение корня уточняют с помощью различных итерационных методов. Суть этих методов состоит в последовательном вычислении значений x0, x1, …, xn, …, которые являются приближениями к корню x*. 2.3. Метод деления отрезка пополам (метод дихотомии, метод бисекции) Метод деления отрезка пополам является самым простым и надежным способом решения нелинейного уравнения. Пусть из предварительного анализа известно, что корень уравнения (2.1) находится на отрезке [a0, b0], т. е. x*  [a0, b0], так, что f(x*) = 0.Пусть функция f(x) непрерывна на отрезке [a0, b0] и принимает на концах отрезка значения разных знаков, т.е. f(a0)f(b0) < 0. (2.2) Разделим отрезок [a0, b0] пополам. Получим точку x0 = 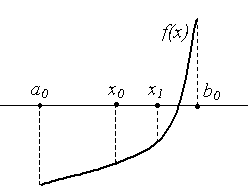 . Вычислим значение функции в этой точке: f(x0). Если f(x0) = 0, то x0 – искомый корень, и задача решена. Если f(x0) 0, то f(x0) – число определенного знака: f(x0) > 0, либо f(x0) < 0. Тогда либо на концах отрезка [a0, x0], либо на концах отрезка [x0, b0] значения функции f(x) имеют разные знаки. Обозначим такой отрезок [a1, b1]. Очевидно, что x* [a1, b1], и длина отрезка [a1, b1] в два раза меньше, чем длина отрезка [a0, b0]. Поступим аналогично с отрезком [a1, b1]. В результате получим либо корень x*, либо новый отрезок [a2, b2], и т.д. (рис. 2.2). Рис. 2.2 Середина n-го отрезка xn =  . Очевидно, что длина отрезка [an, bn] будет равна  , а т. к. x* [an, bn], то| xn – x*|   . (2.3)Погрешность метода. Оценка (2.3) характеризует погрешность метода деления отрезка пополам и указывает на скорость сходимости: метод сходится со скоростью геометрической прогрессии, знаменатель которой q = 1/2. Заметим, что оценка (2.3) является априорной. Критерий окончания. Из соотношения (2.3) следует, что при заданной точности приближения вычисления заканчиваются, когда будет выполнено неравенство bn – an < 2или неравенство n > log2((b0 – a0)/) – 1. Таким образом, количество итераций можно определить заранее. За приближенное значение корня берется величина xn. Пример 2.1. Найдем приближенно x =  с точностью = 0.01. Эта задача эквивалентна решению уравнения x5 – 2 = 0, или нахождению нуля функции f(x) = x5 – 2. В качестве начального отрезка [a0, b0] возьмем отрезок [1, 2]. На концах этого отрезка функция принимает значения с разными знаками: f(1) < 0, f(2) > 0. Найдем число n делений отрезка [1, 2], необходимых для достижения требуемой точности. Имеем: | xn – x*|  =  10-2, n  6.Следовательно, не позднее 6-го деления найдем с требуемой точностью, 1.1484. Результаты вычислений представлены в таблице 2.1.Таблица 2.1
2.4. Метод простых итераций Пусть уравнение (2.1) можно заменить эквивалентным ему уравнением x = (x). (2.4) Например, уравнение  – 0.5 = 0 можно заменить эквивалентным ему уравнением x = 0.5sinx.Выберем каким-либо образом начальное приближение x0. Вычислим значение функции (x) при x = x0 и найдем уточненное значение x1 = (x0). Подставим теперь x1 в уравнение (2.4) и получим новое приближение x2 = (x1) и т. д. Продолжая этот процесс неограниченно, получим последовательность приближений к корню: xn+1 = (xn). (2.5) Формула (2.5) является расчетной формулой метода простых итераций. Если последовательность {xn} сходится при n  , т. е. существуетx* =  xn , (2.6) и функция (x) непрерывна, то, переходя к пределу в (2.5) и учитывая (2.6), получим: x* = xn = (x n -1) = ( xn -1) = (x*). Таким образом, x* = (x*), следовательно, x* – корень уравнения (2.4). Сходимость метода. Сходимость метода простых итераций устанавливает следующая теорема. Теорема 2.2. Если в интервале, содержащем корень x* уравнения (2.4), а также его последовательные приближения x0, x1, …, xn, …, вычисляемые по формуле (2.5), выполнено условие: |'(x)| q < 1, (2.7) то x* = xn.т. е. итерационный процесс сходится и справедлива следующая оценка погрешности: |xn – x*| qn|x0 – x*| (2.8) Оценка (2.8) является априорной. Она показывает, что метод простой итерации сходится со скоростью геометрической прогрессии с знаменателем q. Чем меньше q, тем выше скорость сходимости. Как следует из теоремы 2.2, условие (2.7) является достаточным для сходимости метода простых итераций. Его выполнение гарантирует сходимость процесса (2.5), но невыполнение условия (2.7), вообще говоря, не означает, что итерационный процесс будет расходиться. На рис. 2.3 – 2.6 показаны четыре случая взаимного расположения линий y = x и y = (x) и соответствующие итерационные процессы. Рис. 2.3 и 2.4 соответствуют случаю |'(x)| < 1, и итерационный процесс сходится. При этом, если '(x) > 0 (рис. 2.3), сходимость носит односторонний характер, а если '(x)< 0 (рис. 2.4), сходимость носит двусторонний, колебательный характер. Рис. 2.5 и 2.6 соответствуют случаю |'(x)| > 1 – итерационный процесс расходится. При этом может быть односторонняя (рис. 2.5) и двусторонняя (рис 2.6) расходимость. 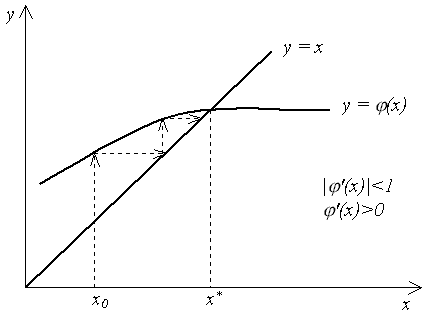 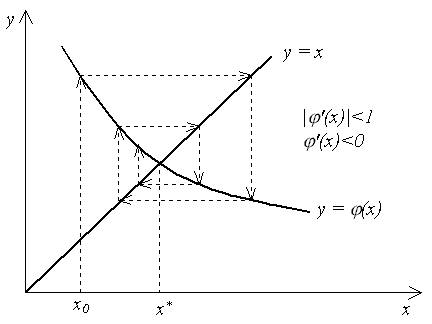 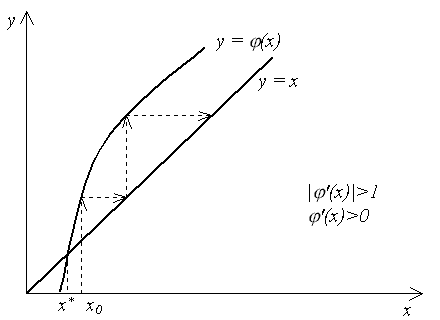 Рис. 2.3 Рис. 2.4 Рис. 2.5 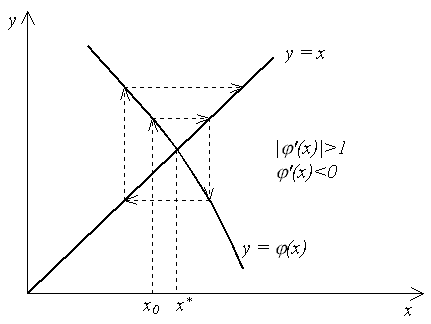 Рис. 2.6 Погрешность метода. Если известна величина q в условии (2.7), то применима следующая апостериорная оценка погрешности: |xn – x*|  |xn – xn – 1|, n > 1. (2.9)Критерий окончания. Из оценки (2.9) вытекает следующий критерий окончания итерационного процесса. Вычисления следует продолжать до выполнения неравенства |xn – xn – 1| <  .Если это условие выполнено, то можно считать, что xn является приближением к x* с точностью . Если q 0.5, то можно пользоваться более простым критерием окончания: |xn – xn – 1| < . (2.10) Пример 2.2. Используем метод простой итерации для решения уравнения f(x) = sin x – x2 = 0с точностью = 0.001. Преобразуем уравнение к виду (2.4): x =  , т. е. (x)= .Нетрудно убедиться, что корень уравнения находится на отрезке [/6, /3]. Например, вычислив значения f(x)на концах отрезка, получим: f(/6)> 0, а f(/3)< 0, т. е. функция на концах отрезка имеет разные знаки, что в соответствии с теоремой 2.1 указывает на то, что внутри отрезка есть корень. Расположение корня наглядно иллюстрирует рис.2.7. 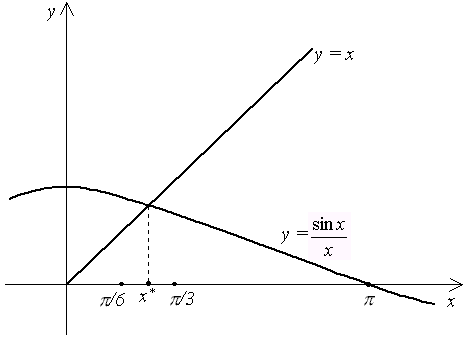 Рис. 2.7 Подсчитаем, первую и вторую производные функции (x): '(x) =  , "(x) =  .Так как "(x) > 0 на отрезке [/6, /3], то производная '(x) монотонно возрастает на этом отрезке и принимает максимальное значение на правом конце отрезка, т. е. в точке /3. Поэтому, справедлива оценка: |'(x)| |'(/3)| 0.312. Таким образом, условие (2.7) выполнено, q < 0.5, и можно воспользоваться критерием окончания вычислений в виде (2.10). В табл. 2.2 приведены приближения, полученные по расчетной формуле (2.5). В качестве начального приближения выбрано значение x0 = 1. Таблица 2.2
Критерий окончания выполняется при n = 5, |x5 – x4| < 0.001. Сходимость двусторонняя, качественный характер такой сходимости представлен на рис. 2.4. Приближенное значение корня с требуемой точностью x*  0.8765.2.5. Метод Ньютона (метод касательных) Метод Ньютона является наиболее эффективным методом решения нелинейных уравнений. Пусть корень x* [a, b], так, что f(a)f(b) < 0. Предполагаем, что функция f(x) непрерывна на отрезке [a, b] и дважды непрерывно дифференцируема на интервале (a, b). Положим x0 = b. Проведем касательную к графику функции y = f(x) в точке B0 = (x0, f(x0)) (рис. 2.8). 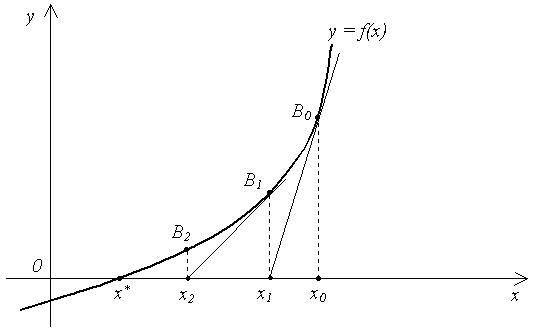 Рис. 2.8 Уравнение касательной будет иметь вид: y – f(x0) = f '(x0)(x – x0). (2.11) Первое пересечение получим, взяв абсциссу точки пересечения этой касательной с осью OX, т. е. положив в (2.11) y = 0, x = x1: x1 = x0 –  . (2.12)Аналогично поступим с точкой B1(x1, f(x1)), затем с точкой B2(x2, f(x2)), и т. д. в результате получим последовательность приближений x1, x2, …, xn , …,причем xn +1 = xn –  . (2.13)Формула (2.13) является расчетной формулой метода Ньютона. Метод Ньютона можно рассматривать как частный случай метода простых итераций, для которого (x) = x -  . (2.14)Сходимость метода. Сходимость метода Ньютона устанавливает следующая теорема. Теорема 2.3. Пусть x* – простой корень уравнения f(x) = 0, и в некоторой окрестности этого корня функция f дважды непрерывно дифференцируема. Тогда найдется такая малая -окрестность корня x*, что при произвольном выборе начального приближения x0из этой окрестности итерационная последовательность, определенная по формуле (2.13) не выходит за пределы этой окрестности и справедлива оценка: |xn + 1 – x*| C |xn – x*|2, n 0, (2.15)где С = -1. Оценка (2.15) означает, что метод сходится с квадратичной скоростью. Сходимость метода Ньютона зависит от того, насколько близко к корню выбрано начальное приближение. Неудачный выбор начального приближения может дать расходящуюся последовательность. Полезно иметь в виду следующее достаточное условие сходимости метода. Пусть [a, b] – отрезок, содержащий корень. Если в качестве начального приближения x0выбрать тот из концов отрезка, для которого f(x)f"(x)0, (2.16) то итерации (2.13) сходятся, причем монотонно. Рис. 2.8 соответствует случаю, когда в качестве начального приближения был выбран правый конец отрезка: x0 = b. Погрешность метода. Оценка (2.15) является априорной и неудобна для практического использования. На практике удобно пользоваться следующей апостериорной оценкой погрешности: |xn – x*| |xn – xn – 1|. (2.17) Критерий окончания. Оценка (2.17) позволяет сформулировать следующий критерий окончания итераций метода Ньютона. При заданной точности > 0 вычисления нужно вести до тех пор, пока не будет выполнено неравенство |xn – xn – 1| < . (2.18) Пример 2.3. Применим метод Ньютона для вычисления  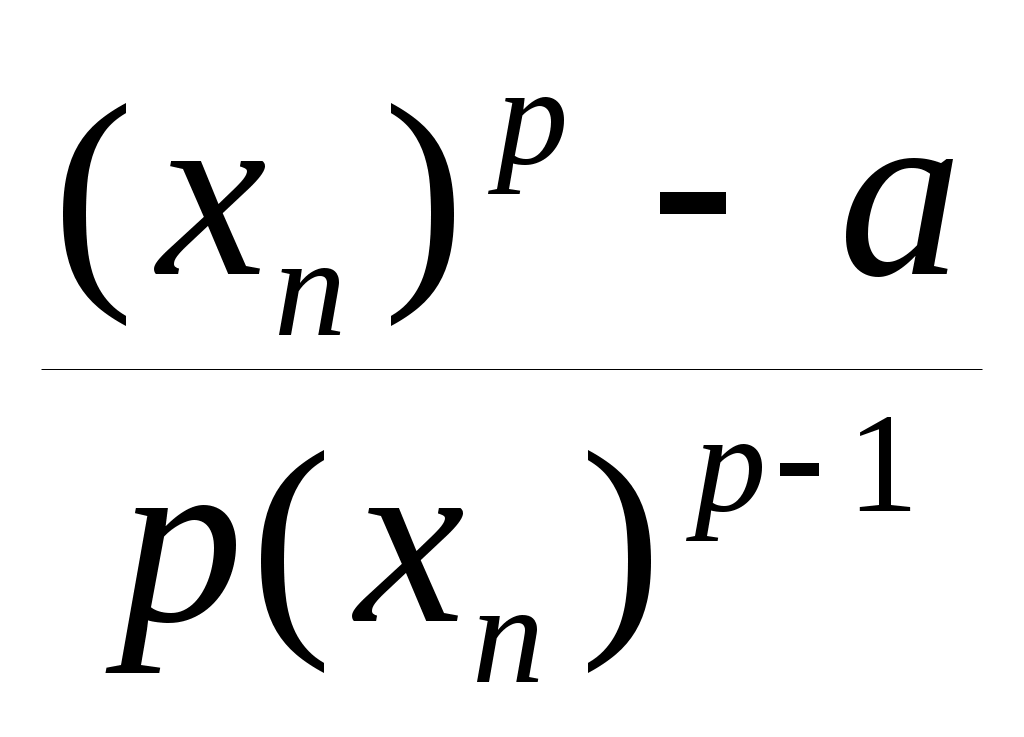. где a > 0, p – натуральное число. Вычисление эквивалентно решению уравнения xp = a. Таким образом, нужно найти корень уравнения f(x) = 0, f(x) = xp– a, f '(x) = pxp – 1. Итерационная формула метода (2.13) примет вид:xn +1 = xn –  =  xn +  . (2.19)Используя формулу (2.19), найдем  с точностью = 10-3.xn +1 =  xn +  .Простой корень уравнения x3 – 7 = 0 расположен на отрезке [1, 2]. Действительно, на концах отрезка [1, 2] функция f(x) = x3 – 7 принимает разные знаки, f (1) < 0, f (2) > 0. Кроме того, при x = 2 выполнено достаточное условие сходимости (2.16): f (2)f" (2)0. Поэтому в качестве начального приближения можно взять x0 = 2. Результаты приведены в табл. 2.3. Таблица 2.3
2.6. Метод секущих (метод хорд) В этом и следующем разделе рассмотрим модификации метода Ньютона. Как видно из формулы (2.13), метод Ньютона требует для своей реализации вычисления производной, что ограничивает его применение. Метод секущих лишен этого недостатка. Если производную заменить ее приближением: f'(xn)  , то вместо формулы (2.13) получим xn +1 = xn –.  . (2.20)Это означает, что касательные заменены секущими. Метод секущих является двухшаговым методом, для вычисления приближения xn +1 необходимо вычислить два предыдущих приближения xn и xn – 1 , и, в частности, на первой итерации надо знать два начальных значения x0 и x1. Формула (2.20) является расчетной формулой метода секущих. На рис. 2.9 приведена геометрическая иллюстрация метода секущих. 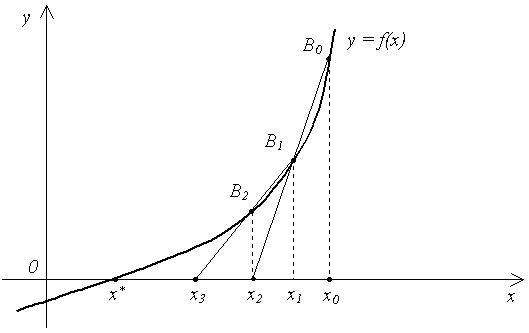 Рис. 2.9 Очередное приближение xn +1 получается как точка пересечения с осью OX секущей, соединяющей точки графика функции f(x) с координатами (xn -1, f(xn - 1)) и (xn , f(xn)). Сходимость метода. Сходимость метода секущих устанавливает следующая теорема. Теорема 2.4. Пусть x* – простой корень уравнения f(x) = 0, и в некоторой окрестности этого корня функция f дважды непрерывно дифференцируема, причем f"(x) 0. Тогда найдется такая малая -окрестность корня x*, что при произвольном выборе начальных приближений x0 иx1из этой окрестности итерационная последовательность, определенная по формуле (2.20) сходится и справедлива оценка: |xn + 1 – x*| C |xn – x*| p, n 0, p =  1.618. (2.21)Сравнение оценок (2.15) и (2.21) показывает, что p < 2, и метод секущих сходится медленнее, чем метод Ньютона. Но в методе Ньютона на каждой итерации надо вычислять и функцию, и производную, а в методе секущих – только функцию. Поэтому при одинаковом объеме вычислений в методе секущих можно сделать примерно вдвое больше итераций и получить более высокую точность. Так же, как и метод Ньютона, при неудачном выборе начальных приближений (вдали от корня) метод секущих может расходиться. Кроме того применение метода секущих осложняется из-за того, что в знаменатель расчетной формулы метода (2.20) входит разность значений функции. Вблизи корня эта разность мала, и метод теряет устойчивость. Критерий окончания. Критерий окончания итераций метода секущих такой же, как и для метода Ньютона. При заданной точности > 0 вычисления нужно вести до тех пор, пока не будет выполнено неравенство |xn – xn – 1| < . (2.22) Пример 2.4. Применим метод секущих для вычисления положительного корня уравнения 4(1 – x2) – ex = 0 с точностью = 10-3. Корень этого уравнения находится на отрезке [0, 1], так как f (0) = 3 > 0, а f (1) = –e < 0. Подсчитаем вторую производную функции: f "(x) = –8 – ex. Условие f(x)f " (x)0 выполняется для точки b = 1. В качестве начального приближения возьмем x0 = b = 1. В качестве второго начального значения возьмем x1= 0.5. Проведем вычисления по расчетной формуле (2.20). Результаты приведены в табл. 2.4. Таблица 2.4
2.7. Метод ложного положения Рассмотрим еще одну модификацию метода Ньютона. Пусть известно, что простой корень x* уравнения f(x) = 0 находится на отрезке [a, b] и на одном из концов отрезка выполняется условие f(x)f"(x)0. Возьмем эту точку в качестве начального приближения. Пусть для определенности это будет b. Положим x0 = a. Будем проводить из точки B = (b, f(b)) прямые через расположенные на графике функции точки Bn с координатами (xn, f(xn), n = 0, 1, … . Абсцисса точки пересечения такой прямой с осью OX есть очередное приближение xn+1. Геометрическая иллюстрация метода приведена на рис. 2.10. 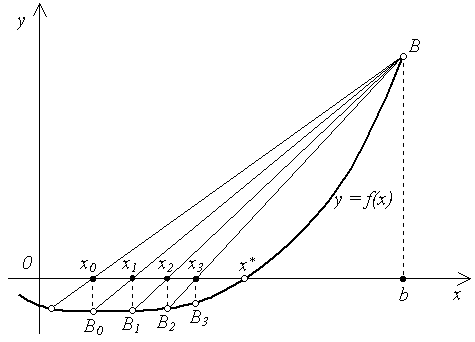 Рис. 2.10 Прямые на этом рисунке заменяют касательные в методе Ньютона (рис. 2.8). Эта замена основана на приближенном равенстве f '(xn)  . (2.23)Заменим в расчетной формуле Ньютона (2.13) производную f '(xn) правой частью приближенного равенства (2.23). В результате получим расчетную формулу метода ложного положения: xn +1 = xn –.  . (2.24)Метод ложного положения обладает только линейной сходимостью. Сходимость тем выше, чем меньше отрезок [a, b]. Критерий окончания. Критерий окончания итераций метода ложного положения такой же, как и для метода Ньютона. При заданной точности > 0 вычисления нужно вести до тех пор, пока не будет выполнено неравенство |xn – xn – 1| < . (2.25) Пример 2.5. Применим метод ложного положения для вычисления корня уравнения x3 + 2x – 11 = 0 с точностью = 10-3. Корень этого уравнения находится на отрезке [1, 2], так как f (1) = –8 < 0, а f (2) = 1 > 0. Для ускорения сходимости возьмем более узкий отрезок [1.9, 2], поскольку f (1.9) < 0, а f (2) > 0. Вторая производная функции f (x) = x3 + 2x – 11 равна 6x. Условие f(x)f"(x)0 выполняется для точки b = 2. В качестве начального приближения возьмем x0 = a = 1.9. По формуле (2.24) имеем x1 = x0 –.  = 1.9 +  1.9254.Продолжая итерационный процесс, получим результаты, приведенные в табл. 2.5. Таблица 2.5
|