Вычислительная математика. Вычислительная_матиматика. Решение задач вычислительными методами. Основные понятия Погрешность

• Название: Решение задач вычислительными методами. Основные понятия Погрешность
• Анкор: Вычислительная математика
• Дата: 02.05.2021
• Размер: 1.45 Mb.
• Имя файла: Вычислительная_матиматика.doc
• Тип: Решение; #200900
• страница: 10 из 10

Темы курсовых работ

Решение нелинейных уравнений

Указание. В курсовых работах 1 – 10 необходимо проанализировать два предложенных метода решения нелинейных уравнений, написать алгоритмы и программы этих методов. С помощью этих программ решить контрольный пример, предварительно локализовав корни уравнения (п. 2.2). Дать сравнительный анализ полученных результатов.

1. Решение нелинейных уравнений методом деления отрезка пополам и методом простых итераций.

Контрольный пример. Найти один действительный корень уравнения x⁵– x – 1 = 0 с точностью = 10^-5.

Указание. При применении метода простых итераций преобразовать исходное уравнение так, чтобы итерационный процесс сходился (п. 2.4).

2. Решение нелинейных уравнений методом деления отрезка пополам и методом секущих.

Контрольный пример. Найти три корня уравнения x³– 4x² + 2 = 0 с точностью = 10^-5.

3. Решение нелинейных уравнений методом деления отрезка пополам и методом Ньютона.

Контрольный пример. Найти три корня уравнения x³+ 3x² – 1 = 0 с точностью = 10^-5.

4. Решение нелинейных уравнений методом деления отрезка пополам и методом ложного положения.

Контрольный пример. Найти три корня уравнения x³+ 3x² – 1 = 0 с точностью = 10^-5.

5. Решение нелинейных уравнений методом простых итераций и методом Ньютона.

Контрольный пример. Найти один действительный корень уравнения x = 0.5 с точностью = 10^-5.

6. Решение нелинейных уравнений методом простых итераций и методом секущих.

Контрольный пример. Найти один действительный корень уравнения x = 0.5 с точностью = 10^-5.

7. Решение нелинейных уравнений методом простых итераций и методом ложного положения.

Контрольный пример. Найти один действительный корень уравнения x = 0.5 с точностью = 10^-5.

8. Решение нелинейных уравнений методом секущих и методом Ньютона.

Контрольный пример. Найти три корня уравнения x³+ 3x² – 3 = 0 с точностью = 10^-5.

9. Решение нелинейных уравнений методом Ньютона и методом ложного положения.

Контрольный пример. Найти три корня уравнения x³+ x² – 10x +8 = 0 с точностью = 10^-5.

10. Решение нелинейных уравнений методом секущих и методом ложного положения.

Контрольный пример. Найти три корня уравнения x³ – x² – 4x +4 = 0 с точностью = 10^-5.
Решение систем линейных алгебраических уравнений

11. Решение системы линейных алгебраических уравнений простым методом исключения Гаусса.

Контрольный пример. Решить систему уравнений
2 .1x₁–4.5x₂– 2.0x₃= 19.07

3.0x₁ + 2.5x₂ + 4.3x₃= 3.21

–6.0x₁+ 3.5x₂ + 2.5x₃= –18.25

12. Решение системы линейных алгебраических уравнений методом исключения Гаусса с выбором главного элемента по столбцу

К онтрольный пример. Решить систему уравнений

1.00x₁ + 0.42x₂+ 0.54x₃ + 0.66x₄= 0.3

0.42x₁ + 1.00x₂ + 0.32x₃+ 0.44x₄= 0.5

0.54x₁+ 0.32x₂ + 1.00x₃ + 0.22x₄= 0.7

0.66x₁ + 0.22x₂ + 1.00x₃– 1.0x₄= 0.9

13. Решение системы линейных алгебраических уравнений методом простых итераций Якоби.

Контрольный пример. Решить систему уравнений с точностью = 10^-5.

– 3.0x₁+0.5x₂+ 0.5x₃ = –56.65

0.5x₁– 6.0x₂ + 0.5x₃ = –160

0.5x₁+ 0.5x₂– 3.0x₃= –210

14. Решение системы линейных алгебраических уравнений методом Зейделя.

Контрольный пример. Решить систему уравнений с точностью = 10^-5.

1 0x₁+2x₂+ x₃ = 10

x₁ + 10x₂ + 2x₃ = 12

x₁+ x₂+ 10x₃= 8

15. Вычисление определителя методом исключения Гаусса.

Контрольный пример. Вычислить определитель det A =

3 .0 1.5 0.1 1.0

0.4 0.5 4.0 6.5

0.3 1.2 3.0 0.7

1.8 2.2 2.5 1.4

16. Вычисление обратной матрицы методом исключения Гаусса.

Контрольный пример. Вычислить обратную матрицу A^-1 для матрицы A =

6.4375 2.1849 –3.7474 1.8822

2.1356 5.2101 1.5220 –1.1234

–3.7362 1.4998 7.6421 1.2324

1.8666 –1.1004 1.2460 8.3312
17. Интерполяция функции многочленами Лагранжа.

Контрольный пример. Построить интерполяционный многочлен Лагранжа для функции y = e по точкам, заданным таблицей

x	0.00	0.25	0.50	0.75	1.00
e	1.0000000	0.9394131	0.7788008	0.7389685	0.3678794

Оценить погрешность интерполяции на отрезке [0, 1]. Вычислить y(0.4) и y(0.8).

18. Метод наименьших квадратов. Линейная и квадратичная аппроксимация
Численное интегрирование функций одной переменной

Указание. В курсовых работах 19 – 22 необходимо проанализировать предложенные методы численного интегрирования функций одной переменной, написать алгоритмы и программы этих методов. С помощью этих программ решить контрольный пример. Проконтролировать погрешность, использовав правило Рунге (п. 5.5). Если можно, вычислить точное значение интеграла. Дать сравнительный анализ полученных результатов.

19. Решение задачи численного интегрирования методом средних, левых и правых прямоугольников.

Контрольный пример. Вычислить , n = 10.

20. Решение задачи численного интегрирования методом средних прямоугольников и трапеций.

Контрольный пример. Вычислить , n = 10.

21. Решение задачи численного интегрирования методом средних прямоугольников и Симпсона.

Контрольный пример. Вычислить , n = 10.

22. Решение задачи численного интегрирования методом трапеций и Симпсона.

Контрольный пример. Вычислить 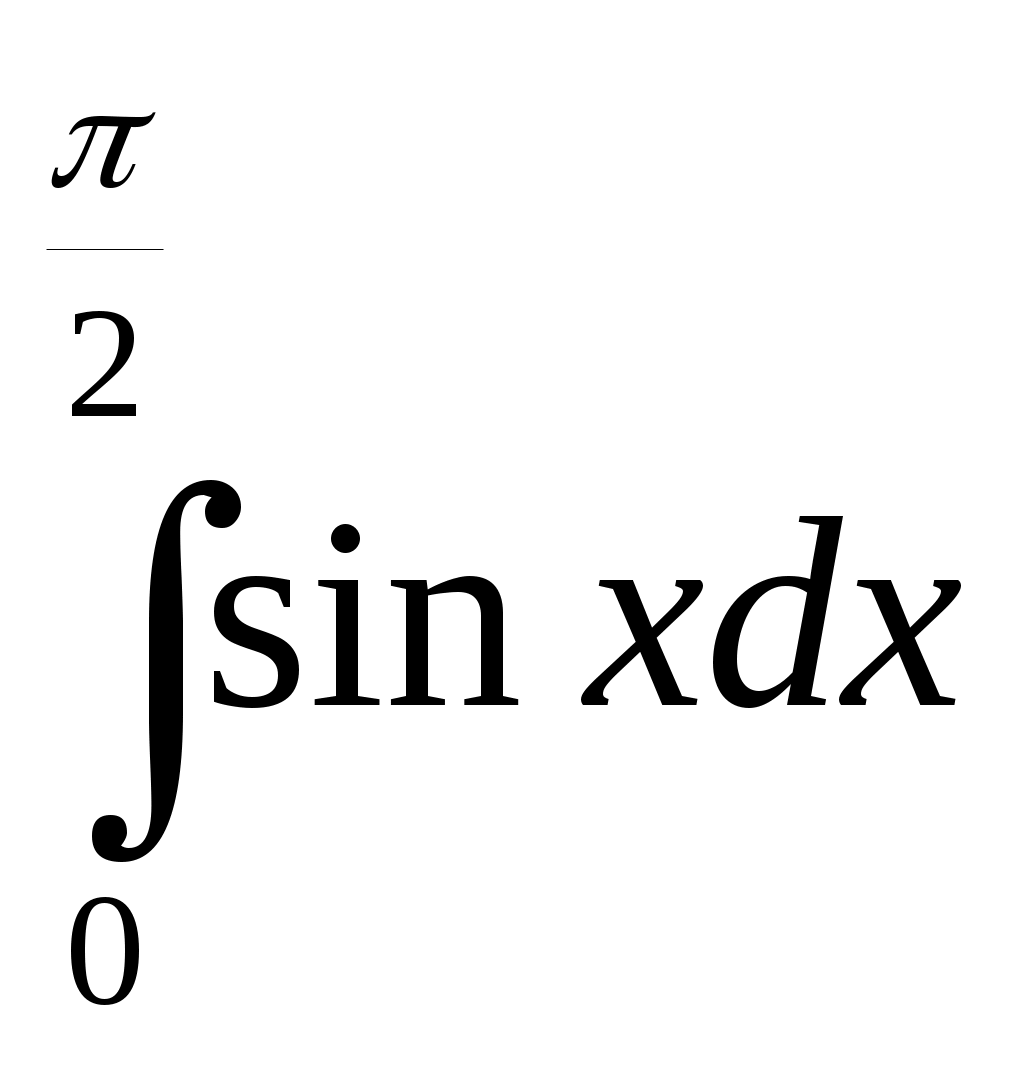, n = 10.

Численное решение дифференциальных уравнений

Указание. В курсовых работах 23 – 26 необходимо проанализировать предложенные методы численного решения задачи Коши, написать алгоритмы и программы этих методов. С помощью этих программ решить контрольный пример. Проконтролировать погрешность, использовав правило Рунге (пп. 6.2, 6.3, 6.4). Найти точное решение. Дать сравнительный анализ полученных результатов.

23. Решение задачи Коши для обыкновенных дифференциальных уравнений простым методом Эйлера и первым модифицированным методом Эйлера.

Контрольный пример. Найти численное решение задачи Коши

y^' = y³, y(0) = 0.5

на отрезке [0, 2] с шагом h = 0.2.

24. Решение задачи Коши для обыкновенных дифференциальных уравнений простым методом Эйлера и вторым модифицированный метод Эйлера – Коши.

Контрольный пример. Найти численное решение задачи Коши

y^' = t², y(0) = 1

на отрезке [0, 2] с шагом h = 0.2.

25. Решение задачи Коши для обыкновенных дифференциальных уравнений первым модифицированным методом Эйлера и вторым модифицированный метод Эйлера – Коши.

Контрольный пример. Найти численное решение задачи Коши

y^' = sint, y(0) = 1

на отрезке [0, 2] с шагом h = 0.2.

26. Решение задачи Коши для обыкновенных дифференциальных уравнений простым методом Эйлера и методом Рунге – Кутта четвертого порядка точности.

Контрольный пример. Найти численное решение задачи Коши

y^' = 2cost, y(0) = 0.

на отрезке [0, 2] с шагом h = 0.2.

Краткие сведения о математиках

Гаусс Карл Фридрих (1777 – 1855) – немецкий математик и физик, работы которого оказали большое влияние на развитие высшей алгебры, геометрии, теории чисел, теории электричества и магнетизма.

Зейдель Людвиг (1821 – 1896) – немецкий астроном и математик.

Коши Огюстен Луи (1789 – 1857) – французский математик, один из создателей современного математического анализа, теории дифференциальных уравнений и др.

Крамер Габриэль (1704 – 1752) – швейцарский математик.

Кутта В. М. (1867 – 1944) – немецкий математик.

Лагранж Жозеф Луи (1736 – 1813) – французский математик, механик и астроном. Один из создателей математического анализа, вариационного исчисления, классической аналитической механики.

Липшиц Рудольф (1832 – 1903) – немецкий математик.

Лейбниц Готфрид Вильгельм (1646 – 1716) – немецкий математик, физик и философ. Один из создателей дифференциального и интегрального исчислений.

Ньютон Исаак (1643 – 1727) – английский физик, механик, астроном, заложивший основы современного естествознания.

Рунге Карл Давид Тольме (1856 – 1927) – немецкий физик и математик.

Симпсон Томас (1710 – 1761) – английский математик.

Тейлор Брук (1685 – 1731) – английский математик и философ. Широко известная формула разложения функции в степенной ряд была получена им в 1712 г.

Эйлер Леонард (1707 – 1783) – математик, физик, механик, астроном. Родился в Швейцарии, с 1726 по 1741 г. и с 1776 по 1783 г. работал в России.

Якоби Карл Густав Якоб (1804 – 1851) – немецкий математик.

Список литературы

1. Амосов А. А. , Дубинский Ю. А., Копченова Н. В. Вычислительные методы для инженеров: Учеб. пособие. – М.: Высш. шк., 1994.

2. Бахвалов Н. С. Численные методы. – М.: Наука, 1973.

3. Волков Е. А. Численные методы. – М.: Наука, 1987.

4. Дьяконов В. П. Математическая система Maple V R3/R4/R5. – М.: Изд-во "СОЛОН", 1998.

5. Калиткин Н. Н. Численные методы. – М.: Наука, 1978.

6. Копченова Н. В., Марон И. А. Вычислительная математика в примерах и задачах. – М.: Наука, 1972.

7. Пирумов У.Г. Численные методы.: Учебное пособие. – М.: Изд-во МАИ, 1998.

- -