Вычислительная математика. Вычислительная_матиматика. Решение задач вычислительными методами. Основные понятия Погрешность
 Скачать 1.45 Mb.
|
|
Тема 3. Решение систем линейных алгебраических уравнений 3.1. Постановка задачи Требуется найти решение системы линейных уравнений: a 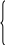 11x1 + a12x2 + a13x3 + … + a1nxn = b1a21x1 + a22x2 + a23x3 + … + a2nxn = b2 a31x1 + a32x2 + a33x3 + … + a3nxn = b3(3.1) ……………………………………………. an1x1 + an2x2 + an3x3 + … + annxn = bn или в матричной форме: Ax = b, (3.2) г  де   a11 a12 a13 … a1n x1 b1 a21 a22 a23 … a2n x2b2 A = a31 a32 a33 … a3n , x = x3 , b = b3 ……………………… … … an1 an2 an3 … ann xn bn По правилу Крамера система n линейных уравнений имеет единственное решение, если определитель системы отличен от нуля (det A  0) и значение каждого из неизвестных определяется следующим образом:xj =  , j = 1, …, n, (3.3)где det Aj – определитель матрицы, получаемой заменой j-го столбца матрицы A столбцом правых частейb. Непосредственный расчет определителей для больших n является очень трудоемким по сравнению с вычислительными методами. Известные в настоящее время многочисленные приближенные методы решения систем линейных алгебраических уравнений распадаются на две большие группы: прямые методы и методы итераций. Прямые методы всегда гарантируют получение решения, если оно существуют, однако, для больших n требуется большое количество операций, и возникает опасность накопления погрешностей. Этого недостатка лишены итерационные методы, но зато они не всегда сходятся и могут применяться лишь для систем определенных классов. Среди прямых методов наиболее распространенным является метод исключения Гаусса и его модификации, Наиболее распространенными итерационными методами является метод простых итераций Якоби и метод Зейделя. Эти методы будут рассмотрены в следующих разделах. 3.2. Метод исключения Гаусса. Схема единственного деления Основная идея метода исключений Гаусса состоит в том, что система уравнений (3.1) приводится к эквивалентной ей системе с верхней треугольной матрицей (прямой ход исключений), а затем неизвестные вычисляются последовательной подстановкой (обратный ход исключений). Рассмотрим сначала простейший метод исключения Гаусса, называемый схемой единственного деления. Прямой ход состоит из n – 1 шагов. На первом шаге исключается переменная x1 из всех уравнений, кроме первого. Для этого нужно из второго, третьего, …, n-го уравнений вычесть первое, умноженное на величину m  =  , i = 2, 3, …, n. (3.4)При этом коэффициенты при x1 обратятся в нуль во всех уравнениях, кроме первого. Введем обозначения: a  = aij – m a1j , b = bi – m b1. (3.5)Легко убедиться, что для всех уравнений, начиная со второго, a 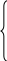 = 0, i = 2, 3, …, n. Преобразованная система запишется в виде: a11x1 + a12x2 + a13x3 + … + a1nxn = b1a  x2 + a x3 + … + a xn = b a  x2 + a x3 + … + a xn = b (3.6)……………………………………………. a  x2 + a x3 + … + a xn = b Все уравнения (3.6), кроме первого, образуют систему (n – 1)-го порядка. Применяя к ней ту же процедуру, мы можем исключить из третьего, четвертого, …, n-го уравнений переменную x2. Точно так же исключаем переменную x3 из последних n – 3 уравнений. На некотором k-ом шаге в предположении, что главный элемент k-ого шага a  0, переменная xk исключается с помощью формул:m  =  , a  = a – m a , b = b – m b , i, j = k + 1, k +2, …, n. (3.7)Индекс k принимает значения 1, 2, …, n – 1. При k = n – 1 получим треугольную систему: 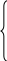a11x1 + a12x2 + a13x3 + … + a1nxn = b1a x2 + a x3 + …+ a xn = b a  x3 + …+ a xn = b (3.8)…………..…………………………. a  xn = b с треугольной матрицей An. Приведение системы (3.1) к треугольному виду (3.8) составляет прямой ход метода Гаусса. При использовании метода Гаусса нет необходимости в предварительном обосновании существования и единственности решения (т. е. доказательства, что det A 0). Если на k-ом шаге все элементы a  (i = k, k +1, …, n) окажутся равными нулю, то система (3.1) не имеет единственного решения.Обратный ход состоит в вычислении переменных. Из последнего уравнения (3.8) определяем xn... Подставляя его в предпоследнее уравнение, находим xn-1, и т. д. Общие формулы имеют вид: xn =  ,xk =  (b - a xk+1 - a xk+2 - … - a xn), k = n – 1, n – 2, …, 1 (3.9)Трудоемкость метода. Для реализации метода исключения Гаусса требуется примерно 2/3n3 операций для прямого хода и n2 операций для обратного хода. Таким образом, общее количество операций составляет примерно 2/3n3 + n2. Пример 3.1. Применим метод исключения Гаусса по схеме единственного деления для решения системы уравнений: 2 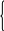 .0x1 + 1.0x2– 0.1x3 + 1.0x4= 2.70.4x1 + 0.5x2 + 4.0x3– 8.5x4= 21.9 0.3x1– 1.0x2 + 1.0x3 + 5.2x4= –3.9 (3.10) 1.0x1 + 0.2x2 + 2.5x3– 1.0x4= 9.9 Будем делать округление чисел до четырех знаков после десятичной точки. Прямой ход. 1-ый шаг. Вычислим множители: m  =  =  = 0.2; m =  =  = 0.15; m =  =  = 0.5.Вычитая из второго, третьего и четвертого уравнений системы (3.10) первое уравнение, умноженное соответственно на m 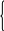, m , m , получим новую систему:2 .0x1 + 1.0x2– 0.1x3 + 1.0x4= 2.70.3x2 + 4.02x3– 8.70x4= 21.36 –1.15x2 + 1.015x3 + 5.05x4= –4.305 (3. 11) – 0.30x2 + 2.55x3–1.50x4= 8.55 2-ой шаг. Вычислим множители: m =  =  = – 3.83333; m =  =  = –1.0.Вычитая из третьего и четвертого уравнений системы (3.11) второе уравнение, умноженное соответственно на m 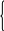и m , приходим к системе: 2.0x1 + 1.0x2– 0.1x3 + 1.0x4= 2.70.3x2 + 4.02x3– 8.70x4= 21.36 16. 425x3– 28.300x4= 77.575 (3.12) 6.570x3–10.200x4= 29.910 3-ий шаг. Вычислим множитель: m  =  =  = 0.4.Вычитая из четвертого уравнения системы (3.12) третье, умноженное на m 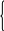, приведем систему к треугольному виду: 2.0x1 + 1.0x2– 0.1x3 + 1.0x4= 2.70.3x2 + 4.02x3– 8.70x4= 21.36 16. 425x3– 28.300x4= 77.575 (3.13) 1.12x4= –1.12 |