Вороненко Соц медицина учебник. Социальная медицина как наука о здоровье общества и охране здоровья
 Скачать 5.8 Mb.
|
|
Взаимосвязь между уровнем перинательного риска у беременных и частотой послеродовых осложнений
 Вывод: между уровнем риска беременных и частотой послеродовых осложнений выявлен сильная, прямая корреляционная зависимость. Ошибка рангового коэффициента корреляции для нашего случая (?30) определяется по формуле:  При большом числе наблюдений (n>30) средняя ошибка рангового коэффициента может быть определена по формуле:  Оценка вероятности коэффициента корреляции проводится по тем же принципам, что используются для другие показателей с расчетом критерия вероятности (t) и учетом числа наблюдений (число степеней свободы вариационных рядов n1=n-2 ). Полученные результаты сравнивают с табличными значениями. В общем, следует помнить, что оценка вероятности результатов коэффициентов корреляции должна превышать свою ошибку не менее чем в 2,5 - 3 раза при достаточном числе наблюдений. Для нашего случая mρ=0,346 и t=ρ/ mρ =0,80/0,346=2,31 , что, соответственно, ниже граничных значений (t =3,2 при p<0,05). Полученный результат (t) не позволяет сделать вывод о вероятности данного рангового коэффициента корреляции. Целесообразно в данном случае использовать большее число наблюдений. Упрощенный метод оценки рангового коэффициента корреляции предвидит сравнение его с критическими табличными значениями для определенного числа пар наблюдений. Коэффициент вероятности значительней вероятности ошибки не более 5% (p<0,05), если пол  учтенный результат выше или равен табличному значению. Для нашего примера для 5 пар наблюдений табличное значение ρ=0,900 (при p<0,05), что выше фактического значения. Итак, полученный результат нельзя считать существенным.Для расчета коэффициента прямолинейности корреляции существует много методов. Они определяются целью, характером и объемом исследований, наглядностью вычислительной техники. Один из методов был предложен К, Пирсоном, в научной литературе известный как линейный коэффициент корреляции Пирсона. Формула его расчета : 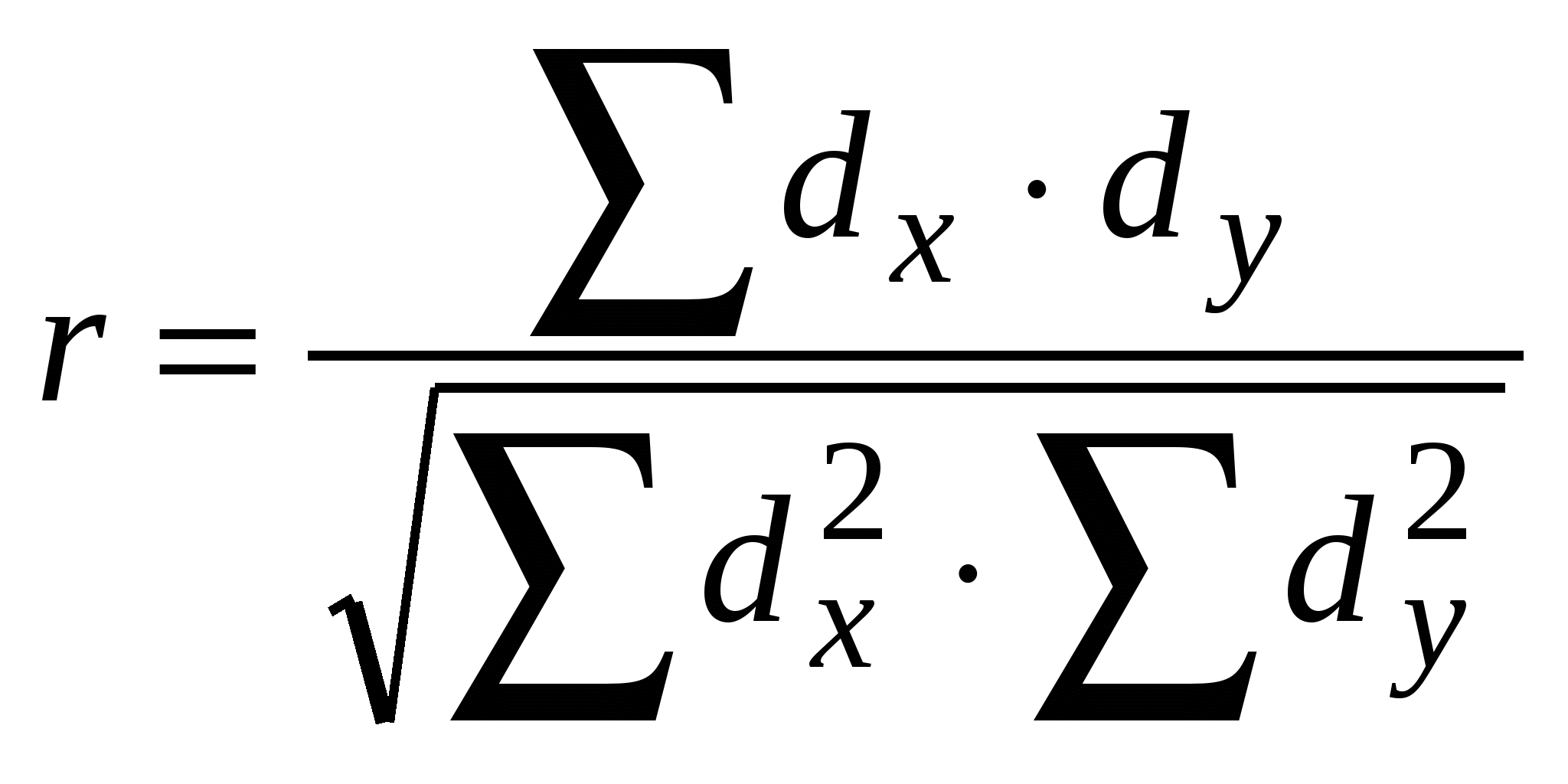 где: х и у - варианты сравниваемых вариационных рядов; dx и dy- отклонения каждого варианта от своей средней арифметической. Например: определить зависимость между продолжительностью заболевания (годы) и частотой выявления хронических бронхитов в молодом возрасте ( до 29 лет). Таблица 3
Расчет линейного коэффициента корреляции:
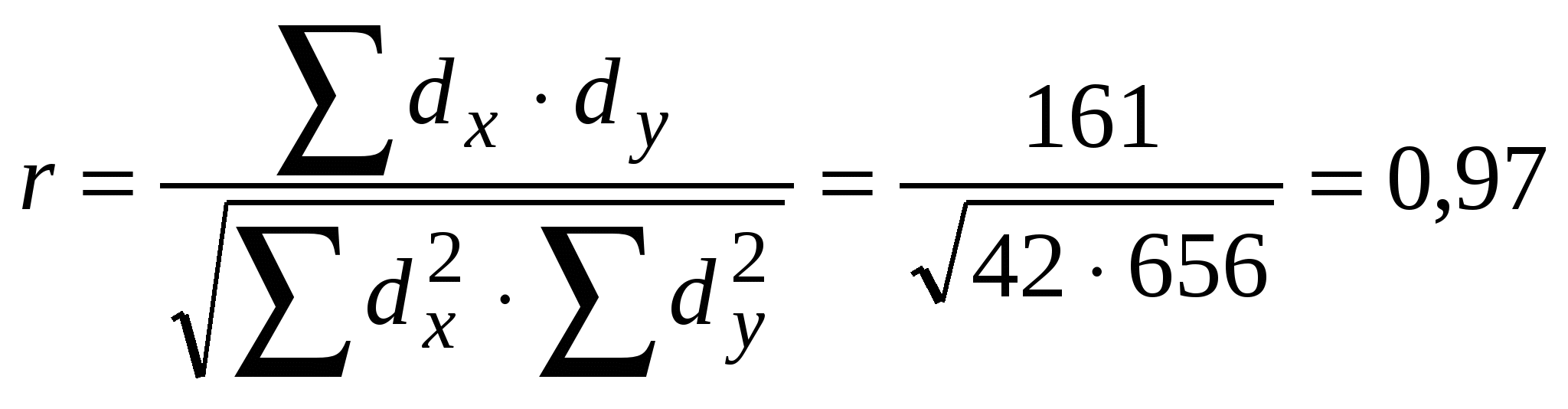 =0,97Вывод: между продолжительностью курения в молодом возрасте и частотой хронических бронхитов существует сильная прямая связь. Вероятность полученного результата определяется взаимоотношением t=r/mr , где mr при малом числе наблюдений (n<30) равно:  Для нашего случая коэффициент вероятности: t=r/ mr =0,97/0,1=9,7. что значительно выше предельно допустимых значений при вероятности ошибки p< 0,05. При большом числе наблюдений (n>30) формула для расчета средней ошибки коэффициента корреляции имеет другой вид:  Прямолинейная корреляционная связь между параметрами характеризуется тем, что каждому из одинаковых измерений одного показателя отвечает определенное среднее значение другого показателя. Данную зависимость можно описать коэффициентом регрессии. Он показывает, на какую величину в среднем изменился другой параметр при изменении первого на определенную единицу измерения. Рассчитывается коэффициент регрессии по формуле:  где  - коэффициент регрессии признаков х по у; - коэффициент корреляции;σx и σy - средние квадратичные отклонения рядов (х) и (у). Рассмотрим использование коэффициента регрессии на примере. При анализе данных физического развития 7-летних мальчиков получены следующие параметры физического развития за ростом (  ) и весом ( ):= 120,0 см; σx = 6,0 см и = 26,0 кг; σy = 2,2 кг; = 0,76. Коэффициент регрессии при данных условиях составляет: Следовательно, при изменении роста на 1 см вес мальчиков в среднем изменится на 0,28 кг. Определенный коэффициент регрессииможно использовать в уравнении регрессии при прогнозировании ситуации, - какой вес в среднем будет отвечать росту мальчиков 125,0 см: Yx = у + (х- ) = 26 + 0,28 (125-120) = 27,4(кг)Коэффициенты регрессии довольно широко используются для построения уравнений регрессии при разработке многих медико-социальных и клинических проблем, в том числе для оценки физического развития детей и подростков. Данные уравнения представляют собой математическую модель, которая описывает характер взаимосвязи между исследуемыми параметрами. Это особенно актуально при построении много факторных моделей и прогнозировании уровней результативного параметра системы при фиксированных уровнях отдельных компонентов (показателей). Приведенные выше методики расчета парных коэффициентов корреляции являются основой и только первым этапом много факторного корреляционного анализа. Парные коэффициенты показывают характер связи (общего, "неочищенного") между исследуемыми параметрами без учета влияния других факторов. Оценка "чистой" взаимосвязи в много факторных моделях определяется на основании парциальних коэффициентов корреляции. Основанием для их расчета являются парные коэффициенты. Множественный коэффициент корреляции отражает связь одновременно комплекса факторов с исследуемым результативным фактором (клиническими показателями и др.). Еще одним параметром много факторного корреляционного анализа является коэффициент детерминации, который отражает удельный вес (%) влияния факторов, которые изучаются (факторные признаки), на уровень результативных признаков (показатели здоровья населения, клинические показатели и другие). Методики практической реализации много факторного анализа не рассматриваются в данном разделе, потому что они являются достаточно объемными и широко приведены в специальной литературе. Учитывая значительные объемы расчетов, реализация много факторного корреляционного анализа не возможна без использования вычислительной техники. Данные методики реализованы во многих пакетах прикладных программ: SPSS, SТАТІSТІСА, SТАDIА, АХUM, MULTIFAC, STATGRAPHICS рlиs, SAS и других, их полноценное использование в клинических и медико-социальных исследованиях не возможно без знаний основ медицинской статистики. Контрольные вопросы 1. Что такое корреляционная связь, чем она отличается от функциональной? 2. Дайте характеристику формы, направленности и силы связи. 3. Какие методы используют для расчета коэффициента корреляции? 4. Как определяется достоверность коэффициента корреляции? 5. Что такое регрессия? 3.11. Основные оценки факторов риска и прогнозирование патологических процессов Невзирая на значительное развитие современной медицины, ко этому времени остаются неизвестными непосредственные причины многих заболеваний или не возможно определить значимость каждой из них за счет их полиэтиологичности. Необходимость практического разрешения указанных проблем стало основой активного развития теории факторов риска. Достаточно частыми в клинической практике являются ситуации, которые требуют определения оптимальной тактики ведения больного, которая базируется на прогнозировании дальнейшего развития патологического процесса, вероятности угрожающих и терминальных состояний. Типичным примером практической реализации данной методики является оценка риска перинатальной патологии, которая широко используется в акушерско-гинекологической практике. При этом в зависимости от бальной оценки по определенным перечням факторов формируются группы риска и корректируется план диспансерного наблюдения за беременными. Принимая во внимание многоплановость данной проблемы, знакомство с теорией факторов риска будет базироваться на однофакторном (парное сравнение групп) или много факторных подходах. Отношение риска, или относительный риск это коэффициент, который позволяет определить риск определенных патологических сдвигов, связанных со здоровьем исследуемых контингентов населения, больных, по сравнению с другими группами, которые отличаются за определенными качественными параметрами (демографическим составом, полом, условиями труда и т.д.). Обязательным для оценки есть наличие двух групп, одно из которых - основная, опытная группа - имеет первоочередной интерес, а друга выступает в роли контрольной (сравниваемой). Отношение между риском патологии в основной опытной (числитель) и контрольной (знаменатель) группах является относительным риском формирования определенного патологического процесса в основной группе относительно сравниваемой. риск для основной группы • 1 О  тносительный риск = риск для контрольной группыИмея информацию, например, об уровнях смертности населения трудоспособного возраста определенного пола от несчастных случаев, отравлений и травм, мы можем определить относительный риск смертности для мужчин относительно к женщинам. При этом значения числителя и знаменателя должны выражаться в одних единицах. Если относительный риск равно 1,0 , мы можем сделать вывод об одинаковом риске смертности для обеих сравниваемых групп. Показатель больше 1,0 свидетельствует о повышенном риске для группы, которая расположена в числителе за счет наличия определенных потенцирующих факторов. Значение коэффициента меньше 1,0 свидетельствует о сниженном риске для основной группы. Например, частота осложнений (риск осложнений) после аппендэктомии при госпитализации в течение 24 часов с момента возникновения патологии составляет 2,1 %, а при госпитализации в срок после 24 часов - 10,8 %. Следовательно, относительный риск осложнений при поздней госпитализации будет составлять: 10,8: 2,1 = 5,14. Это позволяет сделать вывод о существенности влияния на него отмеченного фактора. Общепринятым критерием существенности относительного риска целесообразно брать уровень 3 и выше. Относительный риск количественно определяет взаимосвязь (ассоциацию) между влиянием определенного фактора (сроком госпитализации, методом лечения, полом, условиями труда) и видом патологических сдвигов, поэтому он также имеет названиемера (степень) ассоциации. Приведенная выше методика оценки имеет обобщающий характер и является только одним из элементов анализа. Полноценный анализ прогнозирования патологических процессов, угрожающих состояний, оценки факторов риска не возможен без много факторного подхода к указанной проблеме, который базируется на вероятностном анализе Вальда. Методология статистической оценки вероятности рядом с существующими методами бальной оценки является наиболее оптимальной для практического использования. Она состоит, например, в проведении оценки вероятности определенного перечня симптомов при различных заболеваниях с дальнейшим расчетом вероятности каждого из возможных диагнозов. Разрешение данного задания базируется на основе использование формулы Байеса и основных ее алгоритмов, которые предоставляют возможность рассчитать и оценить достоверность определенного патологического состояния или осложнений по комплексу симптомов у конкретного пациента. Избранный перечень симптомов и признаков не может быть произвольным, а должен состоять только из высоко информативных критериев, которые являются общепринятыми, или отбор которых проводится с привлечением специалистов- экспертов. Их информативность оценивается коэффициентом информативности с использованием информационной меры Кульбака за следующей формулой:  где J(х) - информационная ценность признака; Р(хj./А1) - условная вероятность информационной группы jпризнака х в совокупности исследуемых больных (А1); Р(хj./А2) - условная вероятность информационной группы jпризнака х в совокупности здоровых А2 (контрольная группа). Группы высокого риска (по отдельным видам патологии, осложнениям) формируются на основании расчета прогностических коэффициентов (ПК) для каждой информационной группы. При этом используется разработанная А. А. Генкиним и Е. В. Гублером методика неоднородной последовательной процедуры, которая базируется на последовательном анализе Вальда.  где ПК(хj) - прогностический коэффициент информационной группы и признака х; Р(хj/А1) - условная вероятность информационной группы jпризнака х в совокупности больных с отдельными осложнениями (А1); Р(хj/А2) - условная вероятность информационной группы jпризнака х в контрольной группе А2. В процессе анализа весь первичный массив данных распределяется на отдельные однородные совокупности за клиническими критериями (формами патологических проявлений). Каждой совокупности должна отвечать выделенная в процессе анализа контрольная группа, которой могут быть здоровые лица или больные, которые не имеют соответствующей патологии. Среди отобранных для анализа признаков, кроме клинических факторов, может быть выделенная группа медико-социальных факторов (возраст, профессиональная группа, семейное положение, наследственность, вредные привычки и другие). Заключительное использование их в модели факторов риска обязательно должно быть комплексным. Практическое применение прогностических коэффициентов целесообразно проводить с использованием формализованных учетных документов, где есть информация о наличии и характере конкретных факторов, уровню каждого из которых отвечает определенное значение прогностического коэффициента. Оценка групп риска проводится на основании определения суммы отдельных прогностических коэффициентов, которая сравнивается с табличными значениями. Последние определяются с учетом вероятности ошибочного пропуска группы высокого риска на уровне не больше 5 % (р < 0,05) (погрешность первого рода) и ошибочного отнесения группы низкого риска к группе высокого не больше 10-20 % (р < 0,1-0,2) (погрешность второго рода). При достижении верхнего порога по сумме прогностических коэффициентов оцениваемая группа больных может быть отнесена к контингенту высокого риска, а при достижении нижнего - к контингенту минимального риска за исследуемым фактором. Числовая граница между пороговыми значениями соразмерно делится на три приблизительно равные части: группы сниженного риска, среднего риска, повышенного риску. Это дает возможность формировать прогностические группы риска с промежуточными состояниями, и более дифференцировано подходить к планированию лечебно-профилактических мероприятий. Реализацию данной методики можно представить на следующем примере. Таблица 1 Диагностическая (прогностическая) таблица тяжелых угрожающих состояний у детей при респираторных острых вирусных инфекциях и гриппе
Значительный перечнь клинических критериев, каждый из которых имеет соответствующую градацию, рассчитывают прогностические коэффициенты и информативность признаков. Для оценки отбирают наиболее информативные критерии (коэффициент информативности больше 1). Для определенного ребенка с индивидуальной характеристикой оцениваемого комплекса параметров определяют суммарный прогностический коэффициент, который сравнивают с пороговым табличным значением для определяется вероятности развития угрожающего состояния. Практическая ценность представленной методологии моделирования и прогностической оценки патологических процессов обусловлена ее универсальностью, простотой и возможностью поэтапного использования в течение любого из периодов течения патологии со внесением корректив во врачебной тактике. Контрольные вопросы 1. Что такое относительный риск? 2. На чем базируется теория факторов риска? 3. Что такое погрешность первого и второго рода? Дополнение 1 Критические значения коэффициента корреляции рангов (р) Спирмена (по В. Ю. Урбаху)
Дополнение 2 Таблица значений критерия и (Стьюдента)       Достоверность Число ошибки (р) 0,05 = 5% 0,01 = 1% 0,001 = 0,1% степеней свободы п'________________ ____________ _____________ _ ____1_________12,70_________63,66_____ 637,59_____2__________4,30__________9,92________ 31,60_____ _____3__________3,18__________5,84_________12,94_____ 4__________2,78__________4,60__________8,61_____ 5__________2,57__________4,03__________6,86_____ _____6__________2,42__________3,71__________5,96_____ _____7__________2,36__________3,50__________5,31_____ _____8__________2,31__________3,36__________5,04_____ _____9__________2,26__________3,25__________4,78_____ _____10_________2,23__________3,17__________4,59_____ _____11_________2,20__________3,17__________4,44_____ _____12_________2,18__________3,06______ ___4,32_____  13___ _____2,16_________ _3,01__________4,22 ____ _14________ 2,14__ 2,98_____ 4,14  15________ 2,13_________ _2,95_________ _4,07__________16________ 2,12__________ 2,92_________ _4,02_____ _____17_______ _2,11_________ _2,90__________ 3,96_____ _____18________ 2,10_________ _2,88__________3,92_____ _____19________ 2,09________ __2,86__________3,88_____ _____20_______ _2,09________ __2,84__________3,85_____ _____21_______ _2,08_______ __2,83__________3,82_____ _____22_______ _2,07_______ ___2,82__________3,79_____ _____23________ 2,07__________ 2,81__ ________3,77_____ _____24________ 2,06__________ 2,80___ _______3,75_____ _____25________2,06__________ 2,79___ _______3,73 ______26_____ __2,06__________ 2,78___ _______3,71_____ _____27_______ _2,05__________ 2,77___ _______3,69_____ _____28________ 2,05__________ 2,76___ _______3,67_____ _____29________2,04___ ______ 2,76____ ______3,66__________30______ __2,04_________ 2,75__________3,64_____ ____ _∞________ 1,96__________ 2,58__________3,29______ Дополнение 3 Критические значения 2-числа знаков, которые реже встречаются (по В.Ю. Урбаху)
Нулевая гипотеза принимается при z> z0,5 и не принимается при z < z0,5 Дополнение 4 Критические значения Т-критерий Вилкоксона для взаимосвязанных совокупностей (по В.Ю. Урбаху)    P P P n 0,05 0,01 n 0,05 0,01 n 0,05 0,01 6  1 - 13 18 11 20 53 397 3 - 14 22 14 21 60 44 8 5 1 15 26 17 22 67 50 9 7 3 16 31 21 23 74 56 10 9 4 17 36 24 24 82 62 11 12 6 18 41 29 25 90 69 12 15 8 19 47 33 - - - Нулевая гипотеза принимается при Т ≥Т0,5 и не принимается при Т < Т0,5 , Таблица значений критерия 
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
,
).
р
ероятность