материал для ргр надежность. Содержание лекций Лекция 1

• Название: Содержание лекций Лекция 1
• Анкор: материал для ргр надежность
• Дата: 15.05.2022
• Размер: 1.47 Mb.
• Имя файла: MATERIAL_DLYa_RGR_po_DIAGNOSTIKE (1).doc
• Тип: Лекция; #531012
• страница: 14 из 14

Вопросы для самоконтроля

1. В чем состоит назначение испытаний на надежность? Приведите пример планов испытаний.

2. В чем заключаются задачи определительных испытаний?

3. Каковы задачи первичного эксперимента?

4. Каковы задачи вторичного эксперимента?

5. Как получают статистические данные об отказах элементов?

6. Для чего предназначены определительные испытания?

7. Какие типы планов испытаний применяются чаще всего?

8. По каким признакам выделяют три задачи определительных испытаний, возникающих на стадии обработки данных?

 

Литература

1.Черкесов Г. Н. Надежность аппаратно - программных комплексов. Учебное пособие. - СПб.: Питер, 2005. - 479 с.: ил.

2. Левин В. И. Логическая теория надежности сложных систем. - М.: Эноргоатомиздат, 1985. - 128с.

3. Надежность технических систем: Справочник под редакцией Ушакова И. А. - М.: Радио и связь, 1985. - 608 с.

4. Нечипоренко В. И. Структурный анализ систем (эффективность и надежность). - М.: Сов. радио, 1977. - 214 с.

5. Рябинин И. Л. Черкесов Г. П. Логико - вероятностные методы исследования надежности структурно - сложных систем. - М.: Радио и связь, 1981. - 216 с.

6. Сотсков Б. С. Основы теории и расчета надежности элементовн и устройств автоматики и вычислительной техники. - М.: Высшая школа, 1970. - 270с.

7. ГОСТ 27.002 - 83. Надежность в технике. Термины и определения.

Индивидуальное задание

Анализ надежности системы, как правило, включает следующие операции:

• 
  Анализируются устройства и выполняемые системой и ее составными частями функции, а также взаимосвязь составных частей системы.
  

• 
  Формируется содержание понятия «безотказной работы» для данной конкретной системы.
  

• 
  Определяются возможные отказы составных частей и системы, их причины и возможные последствия.
  

• 
  Оценивается влияние отказов составных частей системы на ее работоспособность.
  

• 
  Система разделяется на элементы, показатели надежности которых известны.
  

• 
  Составляется структурно-логическая схема надежности технической системы, которая является моделью ее безотказной работы.
  

• 
  Составляются расчетные зависимости для определения показателей надежности системы с использованием данных по надежности ее элементов и с учетом структурной схемы.
  

При выполнении индивидуального задания студент оказывается в ситуации, когда выполнены первые шесть пунктов анализа структурной надежности системы, и ему надлежит выполнить заключительный этам анализа - составить расчетные зависимости для определения показателей надежности системы для различных значений наработки t, чтобы графически изобразить вероятность безотказной работы системы Р(t) как функцию наработки.

 

Задание на индивидуальную работу содержит в качестве исходных данных структурную схему надежности системы.

 

Студент выбирает номер структурной схемы (вариант задания) равный номеру, под которым он записан в групповом журнале. Студент заочного факультета номер структурной схемы выбирает по последней цифре номера зачетной книжки.

 

 Вариант 9 Галин (желтые 11 и 12)



  

Вариант 10 Галимова А. (Желтые 10 и 11)



 

 
 Вариант 11 Данилов В.


 Вариант 15 Ильясова Г. (Желтые 2 и 3)



 Вариант 16 Камельянов Р.



 

Вариант 18 Козарез А.



 

 Вариант 19 Ахматгалиев А.



  

 Вариант 25 Низаметдинов (желтый 14й)


 Вариант 26 Хабутдинов Ш.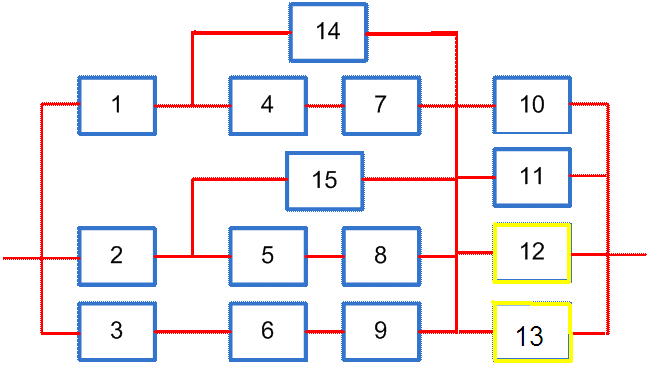



 По структурной схеме надежности системы в соответствии с вариантом задания, требуемому значению вероятности безотказной работы системы γ, % и значениям интенсивностей отказов ее элементов λ , 1/ч , значения которых приведены в таблице:

 

№ вар.	γ, %	Интенсивность отказов элементов, λ · 10-6  ч-1
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	65	0.05	0.25				0.05			0.005		0.1	0.2		0.1	-
2	85	0.1	0.35			0.2			0.01			0.25			0.1	-
3	60	0.03	0.5			0.2			1.0			0.03			0.1	-
4	50	0.1	0.25				0.01		0.05				0.05		0.1	-
5	75	0.05	0.2		0.15									0.2		0.1
6	65	0.02	0.1		0.05					0.08				0.1		0.05
7	70	0.01	0.2				0.1		0.04			0.5			0.1	-
8	50	0.01	0.1		0.02				0.2		0.04			0.5		-
9	85	0.01	0.09		0.30					0.2		0.06			0.1	-
10	80	0.1	1.0		0.05	1.0		0.1			0.3			0.06		0.05
11	95	0.1	0.4		0.06	0.08		0.1		0.2			1.0			0.2
12	60	0.01	1.0												0.1	-
13	75	0.1	0.3		0.5	0.4		1.0	0.35		0.02	0.15		0.5	0.7
14	90	0.1	0.09				0.2						0.3
15	90	0.1	1.0				0.5			0.08		0.5	0.2		1.0
16	80	1.0					0.2	0.5		1.0	0.5	1.0		1.0		0.1
17	70	0.5	0.2		1.0	0.5	1.0	0.5	1.0	0.2		0.5	1.0		0.2
18	60	1.0	0.06			0.04	0.07			0.05	0.01				1.0
19	50	0.5	0.04				0.5	0.05				0.8	0.4	1.0		0.3
20	60	1.0		0.04		0.03	0.15				0.2		0.25			1.0
21	70	0.06			0.35			0,15			0.45			1.0	0.01	0.06
22	80	1.0		0.05					0.08					0.02	1.0
23	90	0.07		0.09				1.0				1.05				1.0
24	80	2.0	1.0	2.0	1.0	1.5		1.2	1.25		0.2	1.0	0.03	1.0	0.5	1.0
25	70	1.0	1.2	0.8	1.0	0.65		0.4	0.08		0.04	1.0	0.2	1.0	1.2	1.0
26	75	0.7			0.55			0,35			0.25			1.1	0.08	0.35
№ вар.	γ, %	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
		Интенсивность отказов элементов, λ · 10-6 ч-1

 
требуется:

• 
  Построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0.1 ÷ 0.2.
  

• 
  Определить γ - процентную наработку системы на отказ.
  

• 
  Обеспечить увеличение γ - процентной наработки на отказ не менее, чем в 1,5 раза за счет: а) повышения надежности элементов; б) структурного резервирования элементов системы.
  

Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов). Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными.

 

Поскольку заданная схема надежности является комбинированной, например:

 



 

ее следует подвергнуть декомпозиции.

 

Метод прямого перебора для таких систем оказывается практически не реализуем. Более целесообразно в этих случаях предварительно произвести декомпозицию системы, разбив ее на простые подсистемы – группы элементов, методика расчета надежности которых известна.

 

Затем эти подсистемы в структурной схеме надежности заменить квазиэлементами с вероятностями безотказной работы, равными вычисленным вероятностям безотказной работы этих подсистем.

 

При необходимости такую процедуру можно выполнить несколько раз, до тех пор, пока оставшиеся квазиэлементы образуют структуру, методика расчета надежности которой также известна.

 

Далее, вводя соответствующие квазиэлементы, преобразовать исходную схему к простейшему виду, например:

 



 

и используя соответствующие формулы, для ряда значений наработки t в предположении простейшего потока отказов вычислить значения вероятностей безотказной работы элементов, квазиэлементов и всей системы в целом.

 В пояснительной записке следует привести все промежуточные преобразования исходной схемы, конкретные рабочие расчетные формулы с их обоснованием, а результаты расчета представить в виде таблицы, в которой по столбцам изменяется значение наработки t, а по строкам в столбцах приводятся вычисленные значения вероятностей безотказной работы элементов, квазиэлементов и всей системы, полученные по рабочим формулам. При этом диапазон измерения наработки t  должен обеспечить снижение вероятности безотказной работы системы до уровня 0.1 ÷ 0.2 и содержать не менее 8 ÷ 10 значений аргумента. Эта таблица может иметь вид:

 

Элемент, квазиэлемент	λ·10-6 ч-1	0,5·106 ч	1,0·106 ч	1,5·106 ч	2,0·106 ч	2,5·106 ч	3,0·106 ч
1 2-5 6,7 8-11 12-15	0,001 0,1 0,001 0,2 0,5	0,9995 0,9512 0,9995 0,9048 0,7788	0,9990 0,9048 0,9900 0,8187 0,6065	0,9985 0,8607 0,9851 0,7408 0,4724	0,9980 0,8187 0,9802 0,6703 0,3679	0,9975 0,7788 0,9753 0,6065 0,2865	0,9970 0,7408 0.9704 0.5488 0,2231
A,B C D,E F G	- - - - -	0,9976 0,9900 0,9909 0,9639 0,9924	0,9909 0,9801 0,9671 0,8282 0,9888	0,9806 0,9704 0,9328 0,6450 0,9863	0,9671 0,9608 0,8913 0,4687 0,9820	0,9511 0,9512 0,8452 0,3245 0,9732	0,9328 0,9417 0,7964 0,2172 0,9583
P	-	0,9561	0,8181	0,6352	0,4593	0,3150	0,2075

 

После этого строится график изменения вероятности безотказной работы системы Р(t) от времени наработки по результатам расчета:



 

 Из него графически по заданному значению γ , % вероятности безотказной работы системы определяется γ - процентная наработка системы на отказ, Tγ , т. е.  время, в течение которого отказ системы не наступит с вероятностью γ , % .

 По заданию требуется предложить два способа увеличения γ - процентной наработки  на отказ в 1.5 раза за счет:

а) повышения надежности элементов системы; 

б) за счет структурного резервирования.

 При повышении надежности системы по первому способу предварительно следует определить элемент или квазиэлемент окончательно преобразованной схемы, повышение надежности которого даст максимальный эффект в отношении надежности всей системы.

Выбор элемента может быть осуществлен по величине вероятности безотказной работы.

 Для дальнейших действий необходимо вычислить требуемое улучшенное значение γ - процентной наработки на отказ Т′ γ  элементарным умножением Tγ на 1.5. Следовательно, чтобы удовлетворить заданию в отношении повышения надежности системы, необходимо обеспечить вероятность безотказной работы P = Pγ за время t=T′ γ = Tγ ·  1.5.

Теперь следует повторить расчет надежности элементов, квазиэлементов и всей системы за время T′ γ  и дополнить этим столбцом предыдущую таблицу:

Элемент квазиэлемент	λ·10-6 ч-1	0,5·106 ч	1,0·106 ч	1,5·106 ч	2,0·106 ч	2,5·106 ч	3,0·106 ч	1,9·106 ч
1 2-5 6,7 8-11 12-15	0,001 0,1 0,001 0,2 0,5	0,9995 0,9512 0,9995 0,9048 0,7788	0,9990 0,9048 0,9900 0,8187 0,6065	0,9985 0,8607 0,9851 0,7408 0,4724	0,9980 0,8187 0,9802 0,6703 0,3679	0,9975 0,7788 0,9753 0,6065 0,2865	0,9970 0,7408 0.9704 0.5488 0,2231	0,9981 0,8270 0,9812 0,6839 0,3867
A,B C D,E F G	- - - - -	0,9976 0,9900 0,9909 0,9639 0,9924	0,9909 0,9801 0,9671 0,8282 0,9888	0,9806 0,9704 0,9328 0,6450 0,9863	0,9671 0,9608 0,8913 0,4687 0,9820	0,9511 0,9512 0,8452 0,3245 0,9732	0,9328 0,9417 0,7964 0,2172 0,9583	0,9701 0,9628 0,9001 0,5017 0,9832
P	-	0,9561	0,8181	0,6352	0,4593	0,3150	0,2075	0,4923

 

Зная вероятности безотказной работы всех элементов преобразованной схемы и требуемое значение Pγ , легко определить, какую вероятность безотказной работы Р′ за время T ′ γ , должен иметь квазиэлемент, избранный для модернизации.

 По первому варианту модернизации необходимо определить интенсивности отказов элементов, входящих в данный квазиэлемент, при которых при неизменной структуре квазиэлемента обеспечивалось бы необходимое значение  P′ ( T′ γ ). Проще это осуществить графоаналитическим методом, задавая ряд пропорционально уменьшенных (по сравнению с исходной) интенсивностей отказов для составляющих квазиэлемента и просчитывая каждый раз величину P′  ( T′ γ   ). Из построенного по этим данным графика можно определить необходимую кратность снижения интенсивности отказов элементов и сами значения интенсивности.  Для найденного решения следует выполнить проверочный расчет вероятности безотказной работы системы за время T′ γ .

 По второму методу надежность выбранного квазиэлемента можно повысить за счет резервирования без изменения надежности составляющих элементов. При этом, учитывая структуру модернизируемого квазиэлемента, нужно выбрать, какие его составляющие элементы и как следует резервировать для достижения наибольшего эффекта. Далее остается определить необходимую кратность резервирования l. Поскольку l есть величина дискретная, аналитически ее определить невозможно.  Для решения задачи нужно последовательно увеличивать кратность резервирования, начиная с единицы, каждый раз по соответствующим формулам определять величину вероятности безотказной работы квазиэлемента в течении времени T′ γ . Как только необходимое значение  P′ γ  ( T′ γ  ) будет обеспечено, окажется реализованным второй метод повышения надежности системы. Для найденного решения также необходимо провести проверку вероятности безотказной работы системы за время T ′ γ . Модернизированную структуру с резервированием следует привести в пояснительной записке, например:

 



 Для построения зависимостей вероятностей безотказной работы от времени для модернизированной системы по первому и второму методу удобно дополнить ранее составленную таблицу соответствующими строками:

 

Элемент квазиэлемент	λ·10-6 ч-1	0,5·106 ч	1,0·106 ч	1,5·106 ч	2,0·106 ч	2,5·106 ч	3,0·106 ч	1,9·106 ч	2,85·106 ч
1 2-5 6,7 8-11 12-15	0,001 0,1 0,001 0,2 0,5	0,9995 0,9512 0,9995 0,9048 0,7788	0,9990 0,9048 0,9900 0,8187 0,6065	0,9985 0,8607 0,9851 0,7408 0,4724	0,9980 0,8187 0,9802 0,6703 0,3679	0,9975 0,7788 0,9753 0,6065 0,2865	0,9970 0,7408 0.9704 0.5488 0,2231	0,9981 0,8270 0,9812 0,6839 0,3867	0,9972 0,7520 0,9719 0,5655 0,2405
A,B C D,E F G	- - - - -	0,9976 0,9900 0,9909 0,9639 0,9924	0,9909 0,9801 0,9671 0,8282 0,9888	0,9806 0,9704 0,9328 0,6450 0,9863	0,9671 0,9608 0,8913 0,4687 0,9820	0,9511 0,9512 0,8452 0,3245 0,9732	0,9328 0,9417 0,7964 0,2172 0,9583	0,9701 0,9628 0,9001 0,5017 0,9832	0,9385 0,9446 0,8112 0,2458 0,9594
P	-	0,9561	0,8181	0,6352	0,4593	0,3150	0,2075	0,4923	0,2352
12′ -15′	0,322	0,8513	0,7143	0,6169	0,5252	0,4471	0,3806	0,5424	0,3994
F′	-	0,9883	0,9270	0,8397	0,7243	0,6043	0,4910	0,7483	0,5238
P′	-	0,9803	0,9157	0,8270	0,7098	0,5866	0,4691	0,7343	0,5011
16-18	0,5	0,7788	0,6065	0,4724	0,3679	0,2865	0,2231	0,3867	0,2405
F′′	-	0,9993	0,9828	0,9173	0,7954	0,6413	0,4858	0,8233	0,5310
P′′	-	0,9912	0,9708	0,9034	0,7795	0,6226	0,4641	0,8079	0,5081

 

 Графики этих зависимостей следует изобразить совместно с графиком изменения вероятности безотказной работы P(t) исходной системы:

 



Полученное семейство кривых позволяет провести сравнение двух вариантов модернизации, которое следует привести в качестве вывода к работе.

 

Пояснительная записка должна быть оформлена в соответствии со стандартом.

 Все действия и использование расчетных соотношений должны быть объяснены и обоснованы. Для заимствуемой информации (формулы, численные значения констант) необходимо указать источник заимствования.

ЛИТЕРАТУРА

1.Черкесов Г.Н. Надежность аппаратно - программных комплексов. Учебное пособие. - СПб.: Питер, 2005.- 479 с.: ил.

2. Левин В.И. Логическая теория надежности сложных систем. - М.: Эноргоатомиздат, 1985.- 128с.

3. Надежность технических систем: Справочник под редакцией Ушакова И.А. - М.:Радио и связь, 1985. - 608 с.

4. Нечипоренко В.И. Структурный анализ систем (эффективность и надежность). - М.: Сов. радио, 1977. - 214 с.

5. Рябинин И.Л.. Черкесов Г.П. Логико - вероятностные методы исследования надежности структурно - сложных систем. - М.: Радио и связь. 1981. - 216 с.

6. Сотсков Б. С. Основы теории и расчета надежности элементов и устройств автоматики и вычислительной техники. М.: Высшая школа,1970. - 270 с.

7. ГОСТ 27.002 - 83. Надежность в технике. Термины и определения.