Курс лекций по Мет.Препод.Матем.. Содержание вопросы общей методики
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
Формы контроля: (поурочный, тематический, итоговый) - устный опрос; - кратковременная самостоятельная работа с целью выявления наиболее трудных для усвоения способов действий, случаев применения ВП, пробелов в знаниях учащихся; - поурочный балл (средства обратной связи); - математический диктант (на этапе формирования автоматизированного навыка); - обучающая, тренировочная самостоятельная работа (закрепление, расширение и углубление знаний, умений; повторение и подготовка к новой теме); - самостоятельная работа на ограниченное время; - проверочная самостоятельная работа (уточнение, учёт уровня знаний); - итоговая контрольная работа; - проверка тетрадей. Средства обратной связи: - сигнальный блокнот; - сигнальные карточки с цифрами; - двухцветная карточка (красный – согласен, зеленый – не согласен). 8. Ознакомление учащихся с приёмами и способами самоконтроля и овладение соответствующими навыками. Приёмы самоконтроля: 1. Проверка по готовому ответу. 2. Круговые примеры. 3. Ответ задан косвенно: сумма ответов, шифровка (кодировка) ответов, занимательные сигналы (свет на табло электрифицированых пособий, арифметическое лото, тематические рисунки). Способы самоконтроля (арифметической проверки): 1. Повторное вычисление тем же, а лучше другим способом (используя разные ВП). 2. Прикидка ответа. 3. По правилам проверки, использование взаимосвязи арифметических действий. +    НАПРИМЕР: 47-19=28 9. Систематическое включение в структуру урока этапа «Устный счет» (математическая разминка). Особенности этого этапа урока: - проводится с разными целями – подготовка; закрепление; формирование ВН; развитие мышления; воспитание интереса к изучению математики и др.; - цель определяет место в структуре урока; - содержание соответствует целям урока, но включает самые разнообразные задания для устных вычислений или логических действий, в том числе занимательный и познавательный материал; - организуется в различных формах: математический диктант; фронтальный опрос с использованием средств обратной связи; дидактическая игра. Организация работы по составлению и заучиванию таблиц План 1. Виды таблиц и возможные пути предъявления их учащимся. 2. Анализ приёмов нахождения табличных результатов. 3. Содержание подготовительной работы к составлению таблиц. 4. Особенности уроков по составлению таблиц. 5. Система работы по закреплению знания таблиц и формированию навыка воспроизведения по памяти табличных результатов. Литература Никифорова С.И. Учим таблицу умножения //НШ-2003-№4. Захарова С.И. Математику учим в игре //НШ-1999.-№8 (из опыта работы). Методическая копилка //НШ.-1999-№8. Сс. 70-74 (стихи, игры, карточки). Закирова Г.Д. Цветовые демонстрационные таблицы умножения //НШ.-1999-№11. 1. Виды таблиц и возможные пути предъявления их учащимся Мы будем говорить одновременно как о таблицах сложения, так и о таблицах умножения, потому что в организации работы с ними нет существенных различий. Составляются сначала таблицы для каждого частного случая, а затем сводные таблицы. Например: умножение числа 3,сложение с переходом через 10 и др. Сводные таблицы могут иметь две формы: 1) по столбцам, 2) прямоугольная таблица Пифагора. ТАБЛИЦЫ   основные производные сложения и умножения вычитания и деления Теоретические основы: смысл Вычитание и деление: смысл операции сложения, определение операций, взаимосвязь умножения с прямыми операциями Сколько таблиц должны запомнить учащиеся? (7 таблиц: 3 основные и 4 производные) Например: 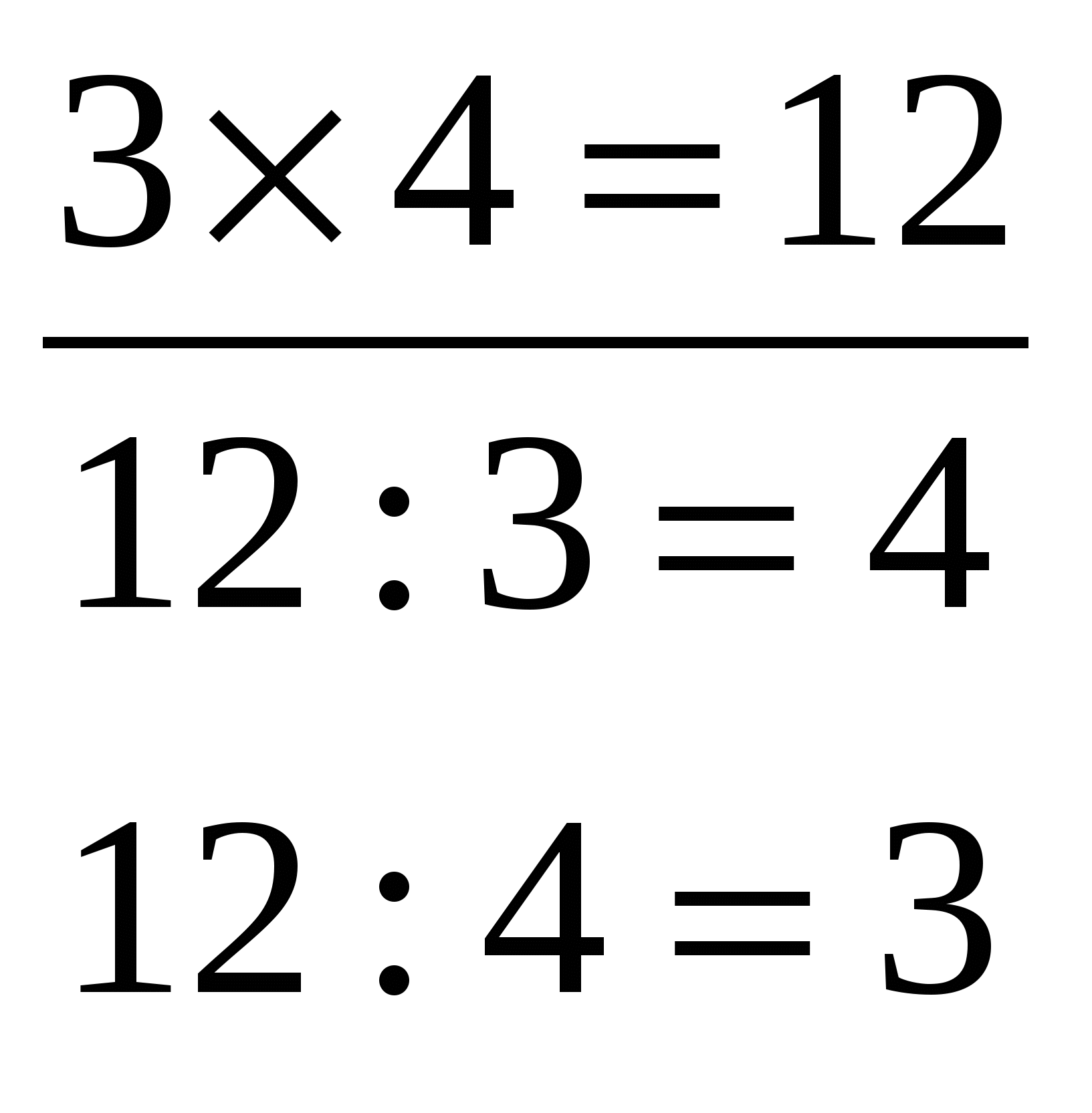 Пути предъявления таблиц: I путь. Даются в готовом виде. От учащихся требуется их механическое запоминание. II путь. Составляются вместе с учащимися. Предполагается деятельностный подход и осознанное запоминание. III путь. Частично вместе с учащимися, частично самостоятельно. Проблема выбора пути I путь в дореволюционной школе. Вспомните метод изучения чисел Грубе, «Арифметику» Магницкого. II путь используется повсеместно уже многие десятилетия. III путь практикуют некоторые учителя по мере овладения учащимися знаниями о способах составления таблиц. Проблема последовательности изучения таблиц для каждого частного случая: а+1 (2,…,9) – по постоянному второму слагаемому; а·2 (3,…,9) или 2 (3,…,9)·а – по постоянному II или I множителю; 2, 3,…, 9 или 9,8,…, 2 или 9, 7, 2…? (традиционная, Пиядин, Давыдов, Истомина). 2. Анализ приёмов нахождения табличных результатов Способы нахождения табличных результатов 1. Эмпирические (практические) – универсальные, но трудоёмкие. Как именно находятся при этом результаты? 2. Логические: а) для сложения и вычитания - прибавление и вычитание по частям, б) для умножения - переход к сложению одинаковых слагаемых, в) для деления - основанный на взаимосвязи деления с умножением. Эти способы тоже универсальные, т.е. применимые к любой паре чисел, но для некоторых пар чисел рациональными являются другие ВП. Например: 3+7, 3·7, 9-6. Как вычислять легче? Способы нахождения табличных произведений: 1) вычисление суммы одинаковых слагаемых; 2) используя предыдущий табличный результат; 3) группировка слагаемых – 2·7=2·5+2·2; 4) перестановка множителей – 2·7=7·2; 5) используя последующий результат – 2·4=2·5-2. А для таблиц сложения? (2; 4; 5) Каждый из названных способов нахождения табличных результатов имеет свое теоретическое обоснование, т.е. ответ на вопрос, почему так можно вычислять, даёт ответ математическая наука. Приёмы сложения и вычитания по частям основаны на правилах: а+(в+с)=(а+в)+с-ассоциативный закон сложения, и а-(в+с) =(а-в)-с правило вычитания суммы из числа Например: 9+4=10+3=13; 12-7=10-5=5     1 3 2 5 По действующей программе уровень овладения учащимися этими правилами – интуитивный, поэтому при составлении таблиц сложения и вычитания используются преимущественно эмпирические методы обучения. Для вычитания как в пределах 10, так и в пределах 20 во многих случаях рациональным является прием, основанный на правиле нахождения неизвестного слагаемого Например: Это правило, переместительные законы сложения и умножения и др. теоретические основы названных ВП рассматриваются в НКМ явно (на экспериментальном или на логическом уровнях), а потому при введении таких ВП используются как эмпирические, так и логические – дедуктивные методы обучения. 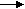 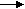 Например: 2·5=10 5·2=10 и таблица начинается с 5·5 Например: 2·5=10 5·2=10 и таблица начинается с 5·518=3·6 18:3=6 и 18:6=3 И на одном уроке можно составить сразу две таблицы деления. 3. Содержание подготовительной работы к составлению таблиц Содержание подготовительной работы к составлению той или другой таблицы определяется исходя из анализа тех ВП, которые будут использоваться для нахождения табличных результатов. Например: а) Сложение в пределах 10 (ОС № 13)  +1 - конкретный смысл сложения, принцип n +1 - конкретный смысл сложения, принцип n +2,3,4 - состав чисел I пятка, предшествующие таблицы. +2,3,4 - состав чисел I пятка, предшествующие таблицы. +5,6,7,8 – переместительный закон сложения (оперативное правило) предшествующие таблицы. +5,6,7,8 – переместительный закон сложения (оперативное правило) предшествующие таблицы.б) Сложение с переходом через 10. Состав чисел первого десятка, сложение в пределах 10, десятичный состав.   9+4= 9+4= 1 3 в) Табличное деление. Конкретный смысл деления, термины, взаимосвязь деления с умножением, правило нахождения неизвестного множителя. Находит ли отражение содержание подготовительной работы в опорных схемах?      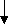  4. Особенности уроков по составлению таблиц 1.Учащиеся привлекаются к активному участию в составлении таблиц. (Предметно-практическая деятельность. Всё, к чему готовы делают самостоятельно. Зона актуального развития.) 2. На уроке используются необходимые средства наглядности. Например, для нахождения табличных произведений: числовые фигуры, записи на доске и в тетради, моделb 1 дм2 и прямого угла. 3. Применяют разные способы нахождения результатов. 4. Обосновывают, доказывают (практическим или логическим способами) правильность вычислений. Например: 7-3=4, 24:4=6 Как доказать? 5. Таблица записывается на доске и в тетради. 6. Заучивание таблиц начинается на этом же уроке. На одном и том же уроке можно составлять только одну таблицу (например: □+2 или 3·□) или связку таблиц (например, □+2 и □-2; 3·□ и □·3, а также две таблицы деления). 5. Система работы по закреплению знания таблиц и формированию навыка воспроизведения по памяти табличных результатов Какую бы методическую систему мы не избрали, работа с учащимися по заучиванию таблиц занимает исключительно важное место. Знание таблиц – это фундамент, база для овладения техникой быстрых и правильных устных и письменных вычислений. Именно этот факт является мотивом для заполнения таблиц. Особенности сохранения и воспроизведения информации, хранящейся в памяти, зависят от того, как организовано запоминание. И непроизвольное, и произвольное запоминание зависят от эмоционального отношения и интереса (удивление, восторг) к изучаемому материалу → создавать благоприятные условия. Например, соревнование с калькулятором, со счетом на пальцах (римская школа). Важным условием запоминания является включение в работу разных видов памяти: зрительной (физиологи утверждают, что зрительный анализатор в 800 раз мощнее слухового); слуховой, образной, словесно-логической (вербальной) → упражнения по таблицам должны быть разнообразны по видам деятельности учащихся: вслух, письменно, с объяснением, в игре и т.п. В воспроизведении табличных результатов типичными являются ошибки памяти учащихся: 1) называют ответ соседнего в таблице примера: 6+4=9, 4·9=32, 32:4=7, 36:9 =5 (36:9=6); 2) смешивают примеры, результаты которых близки в натуральном ряду: 3·7=28, 6·9=56, 7·8=54. Самые трудные для запоминания случаи умножения
Следовательно, их следует чаще включать в содержание обучения. б) произведения с равными значениями: 18= □·□ , 24=□·□, 12=□·□ 3) смешивают правила оперирования с числами 0 и 1: 5·1=6, 5·0=5 и другие подобные случаи. В работе над табличными случаями эффективны те же методические приемы, что и в работе над внетабличными, когда запомнить надо не результат, а способ вычислений, потому что речь идет об одном и том же познавательном процессе – запоминании. Но есть и различия: специальное внимание уделяется отработке знания состава чисел из двух слагаемых; из двух множителей, т.к. это важный шаг к выполнению обратных действий и прочному запоминанию производных таблиц. С этой целью полезно: 1) читать и запоминать табличные равенства слева направо и справа налево: 2·6=12 и 12=2·6; 3+4=7 и 7=3+4; 2) предлагать связки взаимообратных заданий (УДЕ): 3·8= □, 24=□·8, 3·□ =24
Другие специальные приемы в их логической последовательности законспектировать (ксерокопировать) в свою методическую копилку(см.: Медведская В.Н., Гудалина Т.И. Лабораторный практикум, с.94). В Римской школе заучивались только таблицы умножения на числа 2, 3, 4,5. Все остальные произведения находили путем счета на пальцах. Дано: a>5 и b>5. Найти: а·в. Правило. На одной руке и на другой руке вытянуть столько пальцев, на сколько единиц данные числа а и в, каждое в отдельности, превышают 5 (остальные пальцы загнуты). Сумма чисел (количество вытянутых пальцев) дает десятки произведения. К ним надо прибавить произведение чисел, соответствующих числу загнутых пальцев. Например: 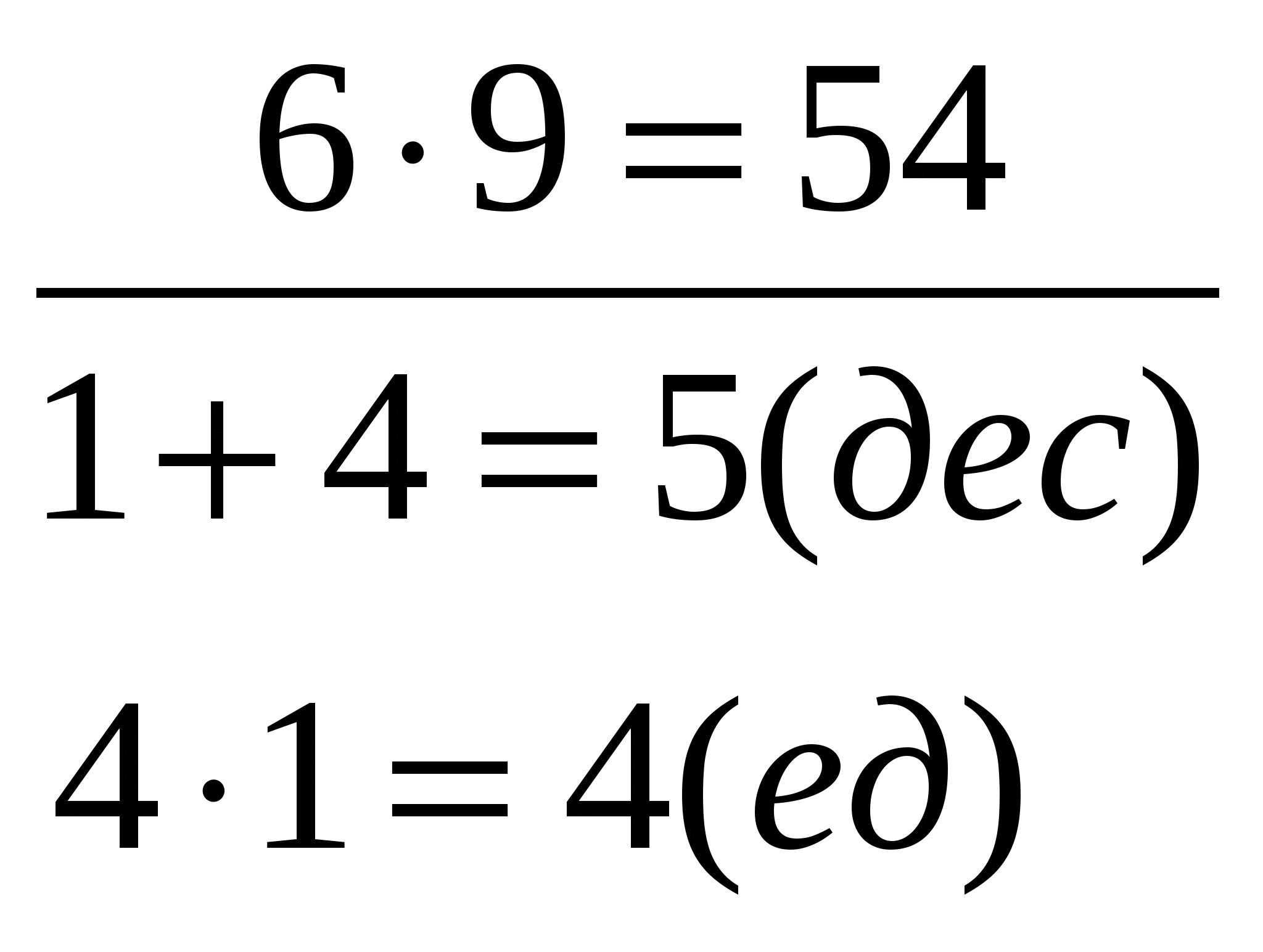 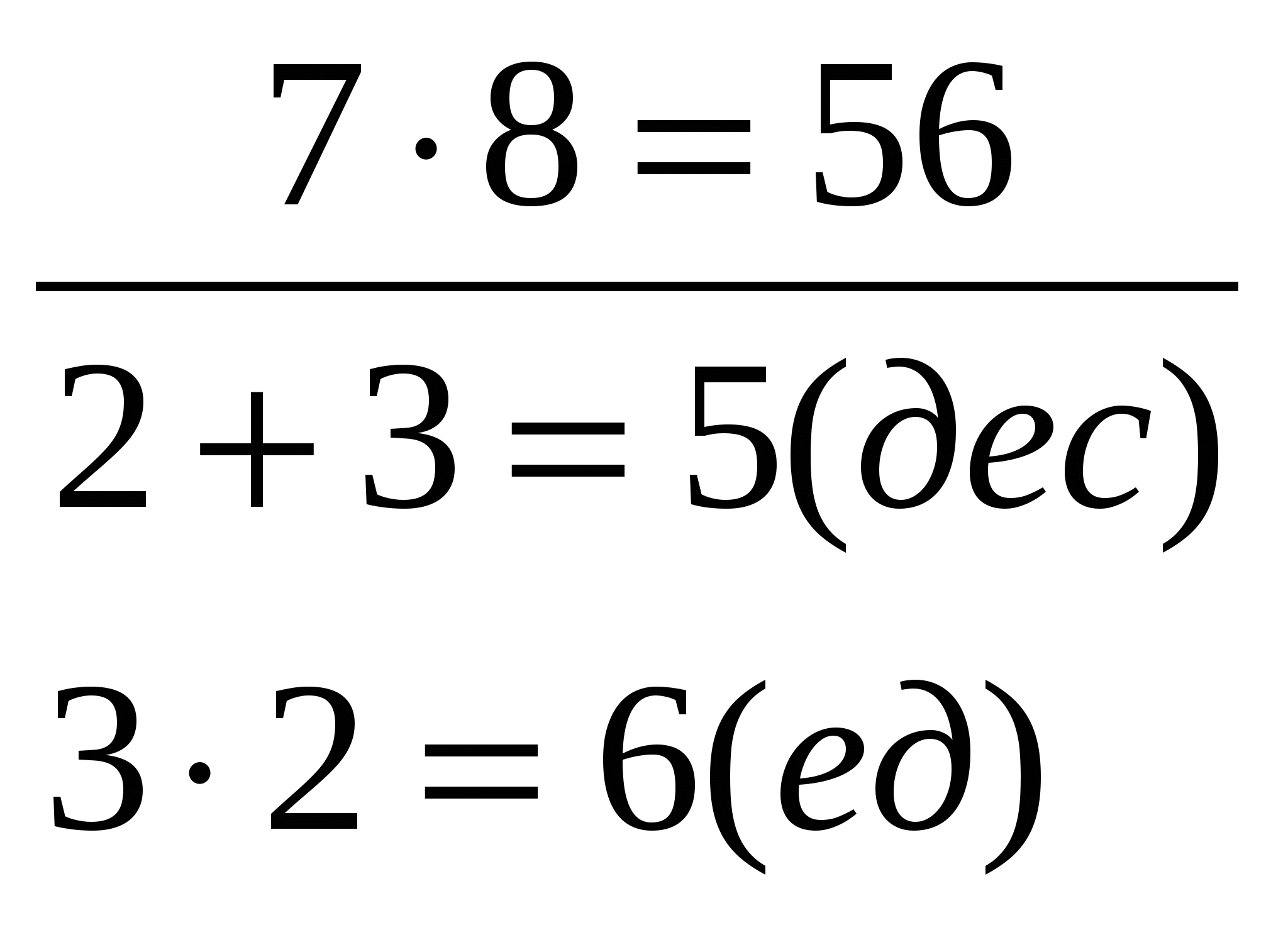 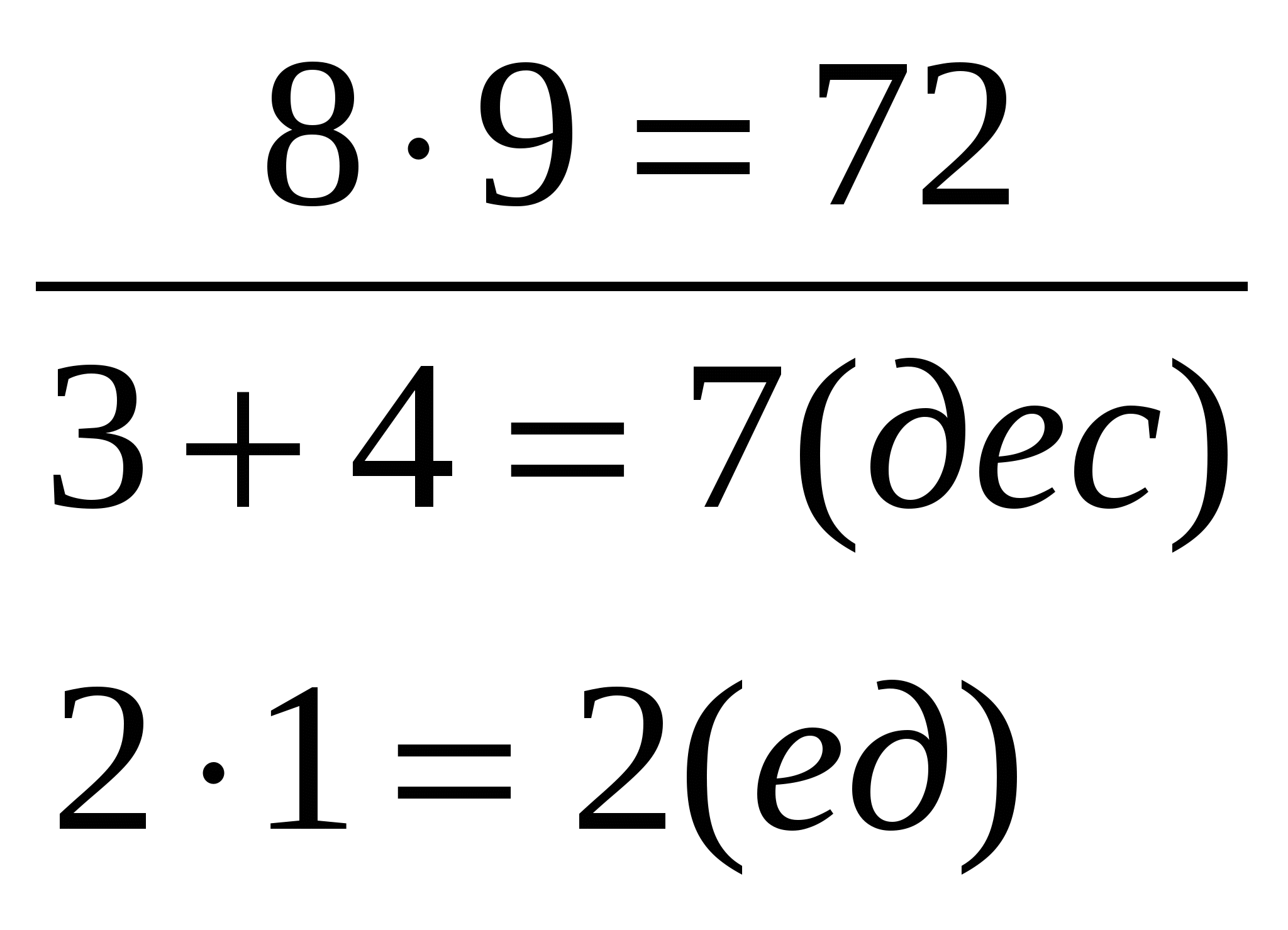 МЕТОДИКА ИЗУЧЕНИЯ НЕАРИФМЕТИЧЕСКОГО МАТЕРИАЛА Методика изучения геометрического материала План 1. Задачи изучения геометрического материала. 2. Содержание геометрического материала в начальном курсе математики. 3. Общие вопросы методики изучения геометрического материала. 4. Система упражнений геометрического характера. Литература Богданова Е.А. Формирование эмпирических предпонятий об основных объектах геометрии // НШ.-2001.-№10. Истомина Н.Б. Методика обучения математике в начальных классах. – М.,1999, п.2.28 1. Задачи изучения геометрического материала Задачи: - формирование пространственных представлений и некоторых геометрических понятий; развитие пространственного воображения; - использование геометрического материала в качестве одного из средств наглядной интерпретации рассматриваемых арифметических фактов, для расширения сферы применения приобретаемых детьми арифметических знаний, умений и навыков (при решении задач геометрического содержания); - вооружение детей практическими навыками измерения длины, площади; - подготовка к изучению систематического курса геометрии. См. Ос №20, четвертый и пятый столбцы. 2. Содержание геометрического материала в начальном курсе математики Содержание: точка, прямая, кривая, отрезок, углы, виды углов, многоугольники и их виды, прямоугольник, квадрат, виды треугольников; окружность, круг; измерение длины, измерение периметра и площади, отношения пересечения, перпендикулярности, параллельности прямых. Геометрические фигуры в начальном курсе математики выступают в двух ролях: а) как дидактическое средство (счётный материал, счётная линейка, модели доли и дроби); б) как предмет изучения (выясняются существенные свойства многоугольников, свойства сторон прямоугольника, определяется понятие «квадрат») См. ОС №20, первый столбец. 3. Общие вопросы методики изучения геометрического материала Геометрические представления у детей начинают складываться ещё до школы и характеризуются, прежде всего, своей конкретностью: каждую геометрическую форму ребёнок связывает с реальным предметом из окружающей обстановки. При обучении в школе необходимо использовать имеющийся опыт детей, уточнять и обогащать их представления. При формировании геометрических представлений важно, чтобы учащиеся твёрдо осознали, что «геометрические фигуры взяты ни откуда-нибудь, а из окружающей действительности», закладывая тем самым основы материалистического миропонимания. Особенности изучения геометрического материала 1. Основными методами изучения являются методы демонстрации, лабораторно-практические работы учащихся (моделирование, вычерчивание, измерение, конструирование, вырезывание), метод наблюдений. Используя эти методы, важно обеспечить разнообразие предлагаемых объектов (отличающихся цветом, размером, материалом, расположением на плоскости), чтобы детям легче было абстрагироваться от конкретных свойств материальных вещей и сконцентрировать своё внимание на существенных признаках объектов, на основе чего и формируются представления о геометрических фигурах. См. Ос№20, второй и четвертый столбцы. Но следует избегать и уклона в грубый эмпиризм : когда вся работа сводится к постановке ряда наблюдений и опытов без достаточного участия мышления, без установления тех связей, которые существуют между изучаемыми фактами. 2. Геометрический материал, по-возможности, рассматривается в неразрывной связи с арифметическим материалом и не выделяется в самостоятельный раздел программы.
Например: а) Подсчет разными способами площади прямоугольника, разбитого на квадраты, даёт основания для вывода равенства ab = ba б) Измерение величин с помощью различных единиц измерения способствуют совершенствованию представлений учащихся о десятичной системе счисления. 3. В изучении геометрического материала реализуется и собственная логика, связанная с введением новых геометрических фигур и рассмотрением их свойств. Например: а) прямоугольник; б) прямой угол; в) свойства прямоугольника; г) измерение площади прямоугольника. 4. Большинство геометрических понятий доводится лишь до уровня представлений, а не их формальных определений. В этой связи на уроках математики в начальных классах не следует задавать вопросы: Что называется прямым углом? Почему этот угол прямой? («потому что у него стороны прямые») Что такое радиус окружности? Учащиеся должны узнавать геометрические фигуры в окружающей обстановке, на рисунке, правильно находить заданную фигуру в наборе геометрических фигур, правильно называть геометрические формы (определение прямоугольника; квадрата; понимание родовидовых отношений). 5. Для дифференциации геометрических понятий широко используется приём сравнения: прямая и отрезок; прямая и кривая; окружность и круг; прямой угол и непрямой. 6. При изучении геометрического материала формируются элементарные навыки черчения. Например: а) начертить отрезок заданной длины; б) построить треугольник, квадрат на клетчатой бумаге; в) построить окружность с помощью циркуля. Число подобных упражнений увеличивается, благодаря аналогичным операциям, выполняемым на уроках труда. 4. Система упражнений геометрического характера Система упражнений геометрического характера: - геометрические объекты для пересчитывания (цель: узнавание и различение геометрических фигур, усвоение терминологии); - формирование представлений о геометрических величинах (длина, площадь) и навыков их измерения; - вычислительные задачи (периметр, площадь); - элементарные построения геометрических фигур на клетчатой бумаге, в том числе с заданными параметрами; - классификация геометрических фигур; - деление фигур на части и составление фигур из частей; - формирование элементарных навыков чтения чертежей (буквенные обозначения); - выяснение геометрической формы предметов или их частей. Приведите примеры упражнений каждого из перечисленных видов. Почему их можно назвать «система упражнений геометрического характера»? |
