Курс лекций по Мет.Препод.Матем.. Содержание вопросы общей методики

• Название: Содержание вопросы общей методики
• Анкор: Курс лекций по Мет.Препод.Матем..doc
• Дата: 16.01.2018
• Размер: 0.7 Mb.
• Имя файла: Курс лекций по Мет.Препод.Матем..doc
• Тип: Документы; #14139
• страница: 3 из 8

Следовательно, задачи выполняют мировоззренческую, дидактическую, развивающую, воспитывающую функции.

4. Система задач, представленных в НКМ
Какие арифметические задачи включать в НКМ?

Как их распределять?

Отбор арифметических задач и система их расположения в НКМ подчинены:

1. 
   логике развёртывания вводимых в начальных классах математических знаний;
   
2. 
   собственной логике ( от простых задач к составным ; от одного
   

типа к другому; сравнение задач разных типов и др.)

В методике принято классифицировать арифметические задачи не только на простые и составные, т. е. по количеству выполняемых при решении действий, но и по другим признакам.

Множество простых задач можно разбить на 4 класса по способу их решения, т.е. по арифметическому действию, которым можно найти ответ на вопрос задачи: на сложение, вычитание, умножение, деление.

Но составим, например, задачи по выражению 4 + 3.

• 
  Что в них общего?
  

- Чем они отличаются?

(Разные теоретические основания для выбора арифметического действия, т.е. разные математические понятия (“ вместе”,“сумма”, “ на больше” в прямой и в косвенной форме, “ уменьшаемое”) или зависимости (как найти уменьшаемое).

Очевидно, что все эти теоретические знания младшие школьники приобретают не сразу в полном объёме, а постепенно, порционно. И каждая такая порция знаний моделируется с помощью текстовых задач.

Составьте теперь задачи с вопросом: “Сколько вместе?”

• 
  Чем они отличаются?
  
• 
  Чем они похожи?
  
• 
  Какой из названных признаков является существенным с точки зрения математики? Обучения математике?
  

(Одинаковая зависимость между данными и искомым.)

По данному основанию можно провести классификацию не только множества всех простых арифметических задач, но и многих составных задач. Такую классификацию называют методической, потому что она имеет непосредственную практическую значимость для учителя – методика работы с задачами каждого класса имеет свою специфику, которую учителю нужно знать и учитывать в процессе обучения младших школьников.

По ОС № 7 назовите типы простых задач, составных задач.

Современная технология обучения решению задач не предполагает заучивание и узнавание учащимися типов задач, т.к. это может привести к формализму знаний.

Обучение общим приёмам работы над задачей
План
1. Особенности современного подхода к обучению решению задач.

2. Общие и операционные цели обучения решению текстовых задач.

3. Использование метода моделирования в обучении решению задач

4. Методы и приёмы:

-осмысления содержания задачи;

-поиска плана её решения.

5. Формы записи решения арифметических задач.

6. Способы проверки арифметических задач.

7. Виды творческих заданий к решенной задаче.
Литература:

Артёмов А.К. Формирование обобщенных умений решать задачи//НШ.-1992.-№2.

Мядзведская В.М. Тэхналогія фарміравання агульных уменняў работы над задачай//ПШ.-2002.-№4.

Медведская В.М. Активизация деятельности учащихся в процессе обучения их решению арифметических задач.- Сб.: Активизация познавательной деятельности младших школьников.- Мн.,1987.

1. Особенности современного подхода
В методической литературе принято выделять два основных вида умения решать задачи:

- общее умение решать любые задачи;

- частное умение, т.е. умение решать задачи определённого вида, определённой математической структуры.

Как строить обучение решению задач:

1) от общего к частному

или

2) от частного к общему?

С 70-х годов ХХ века предпочтение отдаётся первому.


Современная технология обучения решению задач:

Н

акопление опыта решения разнообразных задач как с осознанием процесса и способа их решения, так и на интуитивной основе.





Овладение компонентами общего умения решать задачи в специально организованной для этого деятельности.





Выработка умения решать все предусмотренные программой типы простых задач(частное умение), а затем и составных.


Эта технология реализована, например, в учебниках А.А.Столяра.

Существует ли в практике начального обучения другие технологии?

2. Общие и операционные цели обучения решению текстовых задач
В соответствии с образовательным стандартом и программными требованиями перед учителем стоит цель – научить решать арифметические задачи:


сформировать умение рационально использовать общие приёмы работы над любой задачей, т.е. обучать мыслительной деятельности, осуществляемой в процессе решения задач

научить решать задачи определенных программой (стандартами, учебником) типов



Для достижения этой цели необходима определённая подготовительная работа:

- познакомить с понятием “задача”;

- раскрыть её структуру;

- раскрыть смысл арифметических действий и математических отношений;

- познакомить с величинами;

- раскрыть зависимости между величинами;

- научить выполнять арифметические действия.

Эту нагрузку выполняют простые задачи.

По ОС №8,9,10,11 конкретизируйте цели подготовительной работы для любого типа задач.

Сформулируйте цель работы на втором, на третьем этапах.

Какие требования предъявляются к первым типовым задачам?

Обучение общим приёмам работы над задачей связано с формированием специфических умений, которыми необходимо овладеть, чтобы успешно пройти путь от условия задачи к ответу на её вопрос, т.е. с реализацией комплекса операционных целей: научить читать и слушать задачу; моделировать задачу; и так далее, контролировать свою деятельность.

Работа над любой задачей всегда ведётся по чётко очерченному плану.
План работы над задачей

1. Восприятие и осмысление содержания задачи.

2. Поиск и составление плана решения.

3. Выполнение намеченного плана(решение) и получение ответа на вопрос задачи.

4. Проверка правильности решения.

5. Творческая работа над решённой задачей.

На каждом из этих этапов исользуются свои методы и приёмы работы. Операционные цели соответствуют этим методам и приёмам и определяют содержание и технологию обучения решению задач на конкретном уроке. Например, в зависимости от поставленной учителем цели задачу на данном уроке можно не решать, а только, допустим, провести анализ ее текста или построить к ней чертеж, или построить другую модель, или составить план решения и др.

Соответственно формулировку цели урока «решение задач» следует считать некорректной, так как средство обучения, развития, воспитания равно как и содержание обучения, не может быть целью.
3. Использование метода моделирования в обучении решению задач
"Моделирование" от слова "модель". Модель - любой образ, заместитель, заменитель изучаемого объекта, его аналог, сохраняющий некоторые признаки сходства с оригиналом.

Моделирование (в широком смысле) - один из основных категорий теории познания: на идее изучения моделей различного рода (знаковые, абстрактные, предметные) базируются научные и экспериментальные исследования.

В узком смысле (применительно к школе) моделирование - метод обучения, т.к. это один из возможных и весьма продуктивных способов организации взаимодействия учителя и учащихся.
Сущность моделирования:


замена

Объект познания Модель Текст задачи Модель

перенос выводов

изучение

Использование моделирования в качестве метода обучения органически взаимосвязано с формированием соответствующего метода познавательной деятельности.


Моделирование



метод познания метод обучения

Модель может выступать заменителем оригинала на 4-х уровнях:

1) элементов; 2) структур; 3) функций; 4) результатов.

При изучении абстрактных математических объектов (понятий, отношений, чисел, т.д.) в качестве моделей могут использоваться:

- реальные предметы;

- их изображения (рисунок, макет, муляж, игрушки и пр.);

- условные заменители реальных объектов (круги, квадраты, палочки и др.);

- графическое представление математической ситуации (чертеж, схема).

Использование метода моделирования предполагает решение учителем следующих методических задач:

- подбор или конструирование моделей;

- выбор наиболее оптимальной модели для конкретной учебной ситуации;

- организация познавательной деятельности детей: экспериментальное исследование модели и перенос полученных знаний на оригинал.

Значение моделирования:

1) удовлетворяет потребность в наглядности, связанную с чувственным, опытно-практическим происхождением научных знаний, а также особенностями мышления младшего школьника;

2) позволяет включить, подтолкнуть, направить механизм мышления;

3) управляет процессом познания;

4) приводит к научным открытиям.
Моделирование при обучении решению задач призвано:

1) оказать ученику помощь в представлении себе той жизненной ситуации, которая описана в тексте задачи, в уяснении отношений между описанными в тексте величинами, функциональных зависимостей между данными задачи, между данными и искомым;

2) на этой основе обеспечить осознанный выбор способа решения, нужного арифметического действия, а значит предупредить возможность появления ошибок;

3) обеспечить дифференциацию обучения;

4) найти новые способы решения задачи;

5) обеспечить самоконтроль;

6) развивать мыслительную деятельность: использовать готовые модели как средство добывания новых знаний и создавать самостоятельно свои модели, соответствующие задаче и личным потребностям.
Примеры моделей текстов задач
1. Иллюстрация на наборном полотне – предметное моделирование.

2. Схематический рисунок (Выполните такой рисунок для следующей задачи: «У Коли 7 марок, а у Саши на 3 марки меньше. Сколько марок у Саши?»).

3. Краткая запись задачи (Запишите эту же задачу кратко).

4. Чертеж (Постройте для данной задачи).

5. Знаковая, математическая модель (В нашем примере – это числовое выражение 7-3).

Рассмотрим другую задачу: «Когда от куска отрезали 5м ситца, то в нем осталось 20м. Сколько метров ситца было в куске?»

Какую ошибку могут допустить учащиеся? (20-5=15(м)).

Предупредить ее появление позволит графическая модель:

20 м 5 м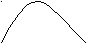








Знаковой, математической моделью этой задачи является: числовое выражение 20+5, а также уравнение Х-5=20.

Нужно ли учить детей моделировать тексты задач, т.е. ставить на уроках соответствующие операционные цели?
Как учить краткой записи

- Сначала для простых задач, а потом для составных.

- Краткая запись выполняется учителем на доске при активном участии класса.

- Заполнение пропусков в готовой схеме краткой записи.

- Составление задач по их краткой записи.

- Самостоятельное выполнение краткой записи в аналогичных задачах.

- Самостоятельное конструирование краткой записи для незнакомых задач.

Формы: таблица; без таблицы, но обязательно по строкам (или столбиком); чертеж (не только для задач на движение).

По краткой записи задачу надо обязательно повторить! Почему?

А. Включить взаимодействие мыслительных операций, анализ – синтез,

Б. Проверить правильность записи и понимания задачи.

Повторение может быть полным (своими словами) текстом задачи или по вопросам: «Что говорится о…? Что показывает …? Что требуется узнать?» и т.п.

В обучении решению задач метод моделирования используется не только на этапе восприятия и осмысления содержания задачи (предметные, условные, схематические, графические модели) или этапе выполнения решения (знаковая модель), но и на этапе поиска плана решения. В качестве модели здесь используется граф-схемы аналитического или синтетического разбора задач, в которых каждый шаг соответствующего рассуждения получает наглядное представление.

4. Методы и приёмы

Какие общие умения необходимы на каждом этапе работы над задачей? Как управлять их формированием?

I. Восприятие и осмысление

Цель: воспринять и понять содержание задачи

Восприятие: на слух (прослушать) или зрительно (чтение).

Итак, прежде всего надо учить слушать и читать задачу.

Как учить слушать задачу

На первых порах всегда дается установка на восприятие, которая является важным регулятором таких психических процессов, как внимание, восприятие, память, мышление.

- Прослушайте (прочитайте) задачу и приготовьтесь ее повторить - от ученика требуется внимание и простое воспроизведение.

-Прослушайте (прочитайте) задачу и приготовьтесь ответить, что в ней известно и что надо найти и назовите в ней главные (опорные) слова - от ученика требуется частичный анализ содержания задачи, дается толчок мысли для обнаружения описываемых в тексте функциональных связей.

- Прослушайте (прочитайте) задачу и подумайте, как ее лучше записать кратко (сделать чертеж, схематический рисунок или использовать другие виды моделей) - от ученика требуется не только концентрация внимания, напряжение памяти, но и аналитико-синтетическая работа мысли.

- Прослушайте задачу и скажите, можно ли сразу ответить на ее вопрос - по ходу прослушивания или самостоятельного прочтения задачи помимо всех предшествующих операций требуется еще выявление описанных в тексте функциональных связей между данными и искомым.

В этой системе установок каждая последующая опирается на навык восприятия задачи предшествующего уровня, в результате чего у учащихся постепенно складывается правильное отношение к работе над текстом задачи, которое характеризуется включением как памяти, так и мышления. Однако установка - это лишь отправной момент, начало движения мысли по пути поиска ответа на поставленный в задаче вопрос. На протяжении всего этого пути от ученика потребуется выполнение целого комплекса умственных действий. Их совокупность и образует интегрированное умение решать задачи.

Как известно, качество целого напрямую зависит от качества и взаимной согласованности составляющих его частей. Поэтому на подготовительном этапе всегда отрабатываются отдельные методы и приемы работы над задачей, а не вся их совокупность; формируются представления, понятия; обобщаются наблюдения и выводятся правила, соответствующие вполне определенному типу задач. Отбор этих частей целостного знания о задачах осуществляется с учетом места изучаемой темы в системе уроков математики и уровня предшествующей подготовки учащихся.

Учитель дает образец чтения: грамотно (словарь!); логические паузы и ударения на опорные слова и числовые данные, на слово «Сколько»; выразительно.

Учить внимательно относится ко всем элементам задачи – еще одна из операционных целей. Для ее достижения используются приемы:

1) задачи – шутки (береза - яблоки);

2) задачи с недостающими данными;

3) задачи с избытком данных;

4) запись некоторых числовых данных не цифрами, а словами и, наоборот, неиспользуемые в решении данные – цифрами;

5) сравнение в чем-то сходных задач


?

I
на ?
– 7 км I – 7 км I – 7 км I – 7 км

II – 4 км II - ? на 4 км больше II - ? в 4 раза больше II – 4 км



прямая форма косвенная форма

Осмысление, т.е. понимание задачи:

о чем в тексте идет речь; что конкретно говорится о …; что известно и что надо найти; как связаны между собой искомое и данные; можно ли сразу ответить на вопрос задачи.

Комплекс приемов первичного анализа задачи зафиксирован в памятке «Как решать задачу» и в дидактическом средстве «Гармошка».

II. Поиск плана решения

Цель: дать ответ на вопрос «Как решить задачу?»

Для простых задач сводится к выбору арифметического действия:

Какое число надо найти: большее или меньшее? Какое действие надо выполнить, чтобы ответить на вопрос задачи. Почему?

Для составных сводится к разбиению на простые задачи, установлению последовательности их решения.

Методы разбора задач

1) от условия к вопросу (синтез);

2) от вопроса к условию (анализ);

3) аналитико-синтетический.

Постройте схемы аналитического и синтетического разбора следующих задач.
Было – 8 корзин по 7 кг

П
380 кг
родали – 5 корзин Мука – 60 пакетов по ? кг

Осталось - ? кг Рис – 40 пакетов по 5 кг


Виды заданий по схемам разбора:

- объяснение по готовой схеме; опора;

- заполнение пропусков в готовой схеме; средство;

- составление задачи по готовой схеме; наглядность.

- построение схемы рассуждений, запись решения и др.
Приемы поиска решения

1. Переформулировка текста задачи (условия или вопроса) в форму, удобную для поиска решения.

2. Сведение новой задачи к задаче знакомого вида.

3. Поиск аналогичных задач.

4. Разбиение текста задачи на смысловые части.

5. Конкретизация (представления, моделирование).

6. Абстрагирование.

7. Уточнение некоторых терминов в тексте задачи.

Оптимальность выбора того или другого метода и приема (или их сочетания) определяется:

- особенностями самой задачи,

- уровнем подготовки учеников,

- планируемыми учителем дидактическими задачами урока

Но в процессе обучения обязательно надо использовать все многообразие приемов.

Почему?

5. Формы записи решения арифметических задач
III. Выполнение решения

Цель: зафиксировать ход решения, выполнить арифметические действия и дать ответ на вопрос задачи.
Решение Ответ

Устно Устно

Печатание Печатание

Запись: Запись

- по действиям (с наименованием Число с наименованием

и без наименования);

- по действиям с краткими

пояснениями; Краткий ответ

- по действиям с вопросами;

- по действиям с планом решения; Полный ответ

-выражением.
Выбор формы записи решения регламентируется:

1) уровнем навыков письма;

2) дидактическими задачами урока.
6.Способы проверки арифметических задач
Цель: проверить правильность хода решения и результатов вычислений; воспитывать привычку самоконтроля, вооружить способами контроля.

Проверка позволяет не только убедиться в правильности решения, но и способствует более глубокому пониманию и осмыслению ее математического содержания, осознанию связей между величинами, представленными в задаче.

Способы проверки:

1.Повторное выполнение решения “Загляни под каждый кустик “ с обоснованием каждого его шага “Задача-цепь, а действия в ней-

звенья. Нельзя звену не придавать

значения”

2.Установление границ ответа “Где искать ключик”

(прикидка) “Что же ждет в конце пути”

3.Установление соответствий между “Подходит ли ключик?”

найденными в результате решения

числами и числами, данными в условии

задачи

4.Решение задачи другим способом и “Мы пойдем другим путем!”

сравнение полученных ответов

5.Составление и решение обратной “С ног на голову”

задачи и сравнение полученного числа

с данными исходной задачи

7. Виды творческих заданий к решенной задаче
Цели творческой работы с решенной задачей самые разнообразные:

1) обобщение способа решения задач;

2) усвоение зависимости между величинами;

3) формирование умения решать задачи определенного типа, определенной математической структуры;

4) совершенствование математических знаний;

5) развитие мышления, функционального мышления;

6) развитие творческого мышления;

7) пробуждение и привитие интереса к изучению математики.

Формы творческой работы:

1.Решение задачи другими способами.

2.Составление (решать необязательно) обратной задачи.

3.Составление аналогичной задачи (Решать?).

4.Преобразование задачи:

- изменение числовых данных, некоторых терминов в тексте и выяснение того, как внесенные изменения повлияют на ход решения, на ответ задачи (решать необязательно!);

- целенаправленное изменение вопроса задачи (решать необязательно!);

- расширение задачи путем введения дополнительны данных и условия, изменение вопроса (продолжить решение).

5.Исследование выполненного решения.