Последний вариант цифровой электроники. Последний вариант цифровой электроники (1). Тема Математическое введение в цифровую технику. 11

• Название: Тема Математическое введение в цифровую технику. 11
• Анкор: Последний вариант цифровой электроники
• Дата: 27.02.2022
• Размер: 2.28 Mb.
• Имя файла: Последний вариант цифровой электроники (1).doc
• Тип: Документы; #375440
• страница: 15 из 16

Глава 10. Аналого-цифровые и цифро-аналоговые преобразователи.

10.1. Дискретизация и квантование, характеристики АЦП и ЦАП.

В большинстве случаев информация о физических процессах и явлениях представляется в аналоговой форме. В аналоговой же форме часто должны формироваться и управляющие воздействия на различные объекты, подвергающиеся анализу, контролю или управлению. Для возможности осуществлять обработку полученной с датчиков аналоговой информации цифровыми методами необходимо выполнить преобразование этой информации к виду, доступному к «пониманию» цифровыми устройствами. Подобное преобразование называется аналого-цифровым. Обратное преобразование, заключающееся в переводе информации, полученной с выходов цифрового устройства к виду непрерывной функции времени или иного ее параметра, называется цифро-аналоговым. Соответственно устройства, выполняющие такие преобразования, называются аналого-цифровыми преобразователями (АЦП) и цифро-аналоговыми преобразователями (ЦАП).

Из рассмотренных ранее типов цифровых устройств очевидно, что входная информация для них должна характеризоваться дискретностью (конечным количеством) своих значений (кодов). Поскольку наиболее удобной формой представления информации для обработки средствами электронных устройств являются напряжения и токи, изменяющиеся во времени, то в качестве дискретных значений этих сигналов можно выбрать как дискретные значения времени, так и дискретные уровни напряжений или токов. На рис. 10.1,а представлена зависимость аналогового напряжения u_а(t) в качестве информационного сигнала, получаемого от объекта с помощью некоторого первичного преобразователя (датчика). Исходный сигнал характеризуется непрерывностью значений как по времени, так и по уровню напряжения. Задав n равных промежутков времени T_д, можно выделить конечную последовательность импульсов с амплитудами u_д(iT_д), где i=1,n, точно соответствующими значениям напряжений u_а(t) в эти моменты времени. Таким образом, реализуется свойство дискретности сигнала по времени. По уровню напряжения дискретизированный по времени сигнал сохраняет свойства непрерывности, поскольку амплитуды u_д(iT_д) могут принимать произвольные значения. Такая форма преобразования аналогового сигнала называется дискретизацией по времени, а время Т_д – периодом дискретизации.

Если в качестве дискретных выбрать m уровней напряжений, то функция u_а(t) вырождается в ступенчатую функцию u_к(jQ), где j=1,m, в которой каждый следующий потенциал отличается от предыдущего на одинаковую величину Q, называемую квантом (рис. 10.1,б). Поскольку функция u_а(t) может иметь произвольную, необязательно линейную форму, то очевидно, что пересечения этой функции с квантованными уровнями jQ будут наблюдаться в неравные промежутки времени t_i=t_i-t_i-1. При этом значения функций u_а(t_i) и u_к(jQ) в моменты времени t_i будут совпадать, а сами моменты времени t_i могут быть произвольными и определяться формой u_а(t) и выбранными уровнями jQ. Отсюда следует, что ступенчатая функция u_к(jQ) сохраняет свойство непрерывности по времени. Такое преобразование аналогового сигнала носит название квантование по уровню.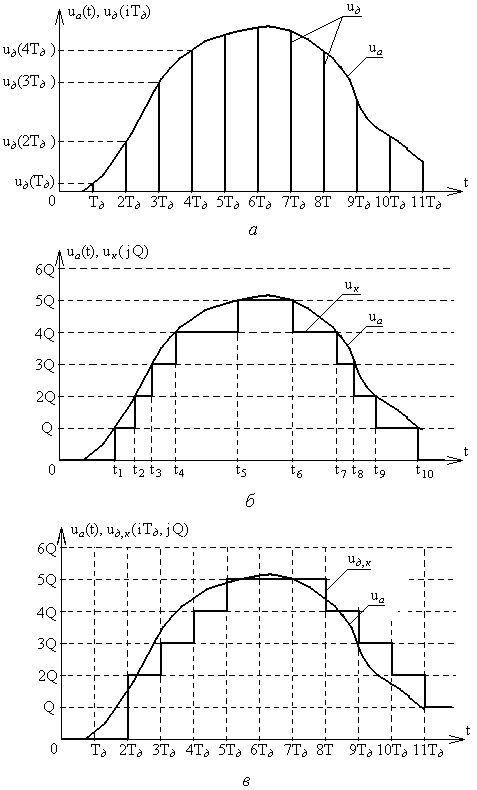


Рис. 10.1. Дискретизация аналогового сигнала по времени (а), квантование по уровню (б), дискретизация и квантование по времени и уровню (в).

Для того, чтобы проведенное преобразование стало аналого-цифровым, в соответствие значению каждого уровня jQ необходимо присвоить цифровой код X_j, в большинстве случаев двоичный. Такой процесс называется кодированием. Обычно цифровой код выбирается равным десятичному эквиваленту номера j квантованного уровня. В этом случае максимальному значению кода соответствует значение максимально возможного входного напряжения АЦП за вычетом одного кванта u_вх.max-Q. Объясняется это тем, что одна кодовая комбинация соответствует нулевому значению входного напряжения АЦП. Рассмотрим основные характеристики устройств аналого-цифрового преобразования.

Разрядность n выходного кода для АЦП и входного для ЦАП – характеризует количество разрядов для отображения аналоговой преобразуемой величины. Эта характеристика определяет количество квантованных уровней m=2ⁿ.

Диапазон входного U_вх. или выходного U_вых. напряжений АЦП или ЦАП соответственно - характеризует полный диапазон входного (выходного) напряжения, которое преобразователь в состоянии отобразить принятым выходным (входным) кодом. Выражается в единицах Вольт. Диапазон данного напряжения может быть как однополярным, так и биполярным в зависимости от типа преобразователя.

Разрешающая способность (чувствительность) – значение минимального изменения входного сигнала АЦП, которое вызывает изменение цифрового кода на единицу. Эта характеристика определяется величиной кванта Q и называется еще величиной младшего разряда (МЗР или LSB в англоязычной терминологии). Из-за наличия неопределенности (погрешности) величиной Q/2 обычно принимается, что изменение цифрового кода на единицу происходит в средней точке диапазона данного квантованного уровня (рис. 10.2,а). Аналогично для ЦАП разрешающая способность – это минимальное изменение выходного аналогового сигнала, обусловленное изменением входного цифрового кода на единицу.

Напряжение смещения нуля U_см.0 – напряжение на входе АЦП, при котором на выходе устанавливается нулевой код. Величина U_см0 определяется сдвигом реальной u_р от идеальной u_ид передаточных характеристик (рис. 10.2,б). Соответственно для ЦАП напряжение смещения нуля – это величина выходного напряжения при нулевом входном коде. Напряжение смещения нуля характеризует аддитивную погрешность преобразователя. Часто U_см.0 выражается в единицах МЗР.

Абсолютная погрешность преобразования в конечной точке шкалы U_f - характеризует отклонение реального максимального входного напряжения для АЦП или выходного для ЦАП от идеального значения, определенного технической документацией преобразователя (рис. 10.2,в). Данная величина определяет угол наклона реальной передаточной характеристики и мультипликативную погрешность преобразователя. Также как и U_см.0 часто выражается в единицах МЗР.

Интегральная нелинейность U_L - характеризует максимально возможное отклонение реальной передаточной характеристики АЦП (ЦАП) от заданной идеальной при нулевых значениях U_см.0 и U_f (рис. 10.2,г). Выражается в единицах МЗР или в процентах по отношению к максимальному входному (выходному) напряжению преобразователя.

Дифференциальная нелинейность U_диф. - характеризует максимальное отклонение величины одного из квантов АЦП (ЦАП) от идеального аналогового значения Q (рис. 10.2,д). Выражается в единицах МЗР или в процентах по отношению к максимальному входному (выходному) напряжению. Если дифференциальная нелинейность АЦП превышает 1 МЗР, то в выходном коде могут выпадать одна или несколько кодовых комбинаций Х_вып. Аналогично если дифференциальная нелинейность ЦАП превышает 1 МЗР, то в выходном напряжении могут выпадать один или несколько квантованных уровней.

Время преобразования t_сдля АЦП - характеризует временной интервал с момента подачи управляющего сигнала «начало преобразования» и до момента получения на выходе адекватного цифрового кода. Изменение входного аналогового сигнала в период времени t_c нежелательно, поскольку это изменение вносит неопределенность в генерируемый выходной код. Для ЦАП аналогичный параметр носит название времени установления t_s выходного аналогового сигнала. Очевидно, что входной цифровой код в данный период времени должен оставаться неизменным.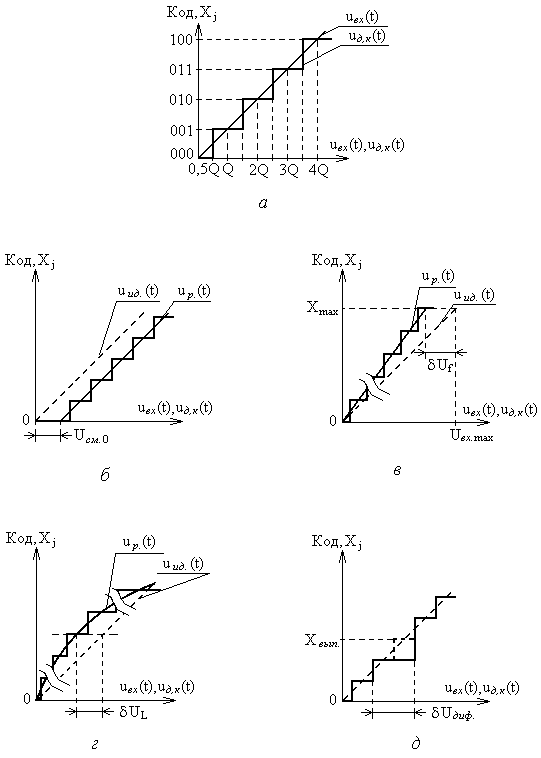



Рис. 10.2. Пояснения к характеристикам АЦП: (а) - разрешающая способностьQ, (б) - напряжение смещения нуля U_см.0, (в) - абсолютная погрешность преобразования в конечной точке шкалы U_f, (г) - итегральная нелинейность U_L, (д) - дифференциальная нелинейность U_диф.

Максимальная частота преобразования f_с.max - определяет максимальное значение числа отсчетов входного сигнала, выполняемых преобразователем в единицу времени при сохранении полной точности. Если входной аналоговый сигнал АЦП можно представить в виде конечной суммы гармонических составляющих, т.е. конечным частотным спектром , то выбор f_c определяется теоремой Котельникова. Согласно этой теореме частоту преобразования АЦП следует выбирать большей или равной удвоенной частоте f_k максимальной гармоники входного аналогового сигнала:

,

где .
10.2. Цифро-аналоговые преобразователи.

10.2.1. ЦАП с матрицей из взвешенных резисторов.

При построении ЦАП широкое распространение получил принцип суммирования токов, поступающих из цепей, каждая из которых отражает состояние текущего разряда двоичного кода. На рис. 10.3 представлена схема ЦАП с суммированием токов с матрицей из взвешенных резисторов. Транзисторы VT_i выполняют роль ключей и управляются разрядами X_i входного цифрового кода. Поскольку входное дифференциальное напряжение операционного усилителя ОУ принимается равным нулю (его прямой и инверсный входы эквипотенциальны), а его прямой вход привязан к нулевому потенциалу общего провода, то и на инверсном входе ОУ также присутствует нулевой потенциал. Поэтому, при наличии логической единицы в разряде X_i, на затвор соответствующего полевого транзистора VT_i поступает положительный отпирающий потенциал логической единицы. В результате чего транзистор открывается и замыкает соответствующую цепь с резистором R/2ⁱ на вход ОУ. При наличии логического нуля в разряде X_i данный транзистор закрыт и соответствующая цепь разомкнута.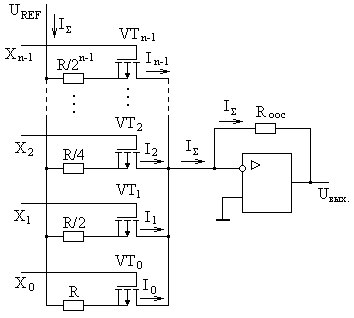



Рис. 10.3. Схема ЦАП с матрицей из взвешенных резисторов.

Считая, что потенциал на инверсном входе ОУ равен нулю по причине эквипотенциальности его входов, величина тока I_i в каждой из i-ой цепи при замыкании соответствующего ключа определяется номиналом R/2ⁱ сопротивления в этой цепи:

;

;

………………….

;

…………………

,

где U_REF – постоянное стабильное опорное напряжение.

Считая, что все ключи находятся в замкнутом состоянии (во всех разрядах X_i присутствуют логические единицы), суммарный ток I_, образованный суммой втекающих в один узел токов I_i, равен:



.

Поскольку для ОУ величина входного сопротивления для дифференциального сигнала велика и в первом приближении принимается равной бесконечности, то весь ток I_, минуя ОУ, втекает в цепь отрицательной обратной связи с резистором R_оос. Тогда для U_вых можно записать:

.

Знак «-» перед выражением для U_вых является признаком подачи сигналов на инвертирующий вход ОУ. В случае произвольного кода X, т.е. при различных состояниях транзисторов VT_i, выражение для U_вых примет вид:

,

где X_i принимает значение нуля или единицы в зависимости от входного двоичного кода.

Из полученной формулы очевидно, что напряжение на выходе ЦАП пропорционально двоичному коду на входе и не зависит от сопротивления нагрузки. Недостатком приведенной на рис. 10.3 схемы является необходимость использования резисторов матрицы с номиналами, изменяющимися в широком диапазоне от R до R/2^n-1. Кроме того, номиналы этих резисторов должны выдерживаться с прецизионной точностью. Также в данной схеме существенное влияние на точность преобразования оказывают сопротивления каналов открытых ключей на транзисторах VT_i, поскольку каналы транзисторов образуют последовательное соединение с резисторами матрицы. Для минимизации погрешности преобразования, сопротивления резисторов матрицы должны быть много больше сопротивлений открытых каналов транзисторных ключей. Также для снижения влияния сопротивления открытых ключей токовые цепи с i-ми весовыми резисторами формируют на основе токостабилизирующих двуполюсников, что в значительной степени усложняет схему.
10.2.2. ЦАП с матрицей R-2R.

На практике большее распространение получила схема, использующая резистивную матрицу R-2R (рис.10.4), особенно в случае многоразрядных ЦАП. Номиналы всех резисторов в такой схеме ограниченны только двумя значениями R и 2R. В схеме предусмотрены переключающие ключи на транзисторах VT1_i и VT2_i в каждом разряде. При подаче на разрядный вход X_i логического нуля положительным отпирающим потенциалом логической единицы с выхода инвертора ЛЭ_i открывается транзистор VT2_i. Соответствующая цепь резисторной матрицы с резистором номиналом 2R замыкается на нулевой потенциал общего провода. Транзистор VT1_i при этом остается закрытым. Если на вход X_i подан потенциал логической единицы, то транзистор VT2_i оказывается закрытым, а транзистор VT1_i - открытым. Таким образом, ток из i-ой цепи резистивной матрицы попадает в цепь отрицательной обратной связи ОУ.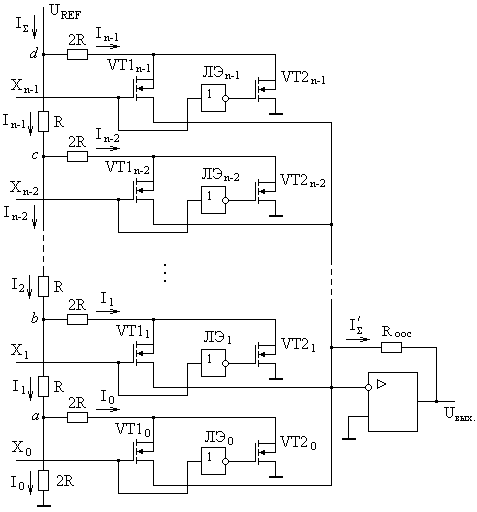



Рис. 10.4. Схема ЦАП с матрицей R-2R.

В отличие от схемы рис. 10.3, в которой ток I_i через соответствующую цепь в зависимости от состояния ключа VT_i либо протекает, либо не протекает, в схеме рис. 10.4 ток I_i присутствует всегда. Разрядными ключами (VT1_i, VT2_i) осуществляется коммутация этого тока либо в общий вывод нулевого потенциала источника питания, либо в цепь отрицательной обратной связи ОУ с резистором R_ooc. Входное сопротивление инверсного входа ОУ, охваченного отрицательной обратной связью, равно:

,

где K_оу – коэффициент усиления по напряжению операционного усилителя без обратной связи. Считая, что K_оу, можно принять, что R_вх.оос0. Тогда ток I_i, втекающий как в общий провод нулевого потенциала, так и в цепь обратной связи с R_оос в зависимости от значения разряда X_i, можно считать одинаковым по величине в обоих случаях.

Принцип организации резистивной матрицы R-2R заключается в том, что входное сопротивление относительно разрядных узлов матрицы (a, b, c, d) всегда равно R. Для наглядности примем, что во всех разрядах X_i присутствуют логические нули, т.е. все цепи 2R резисторной матрицы замкнуты на землю. Тогда входное сопротивление относительно узла а есть параллельное соединение двух резисторов 2R: 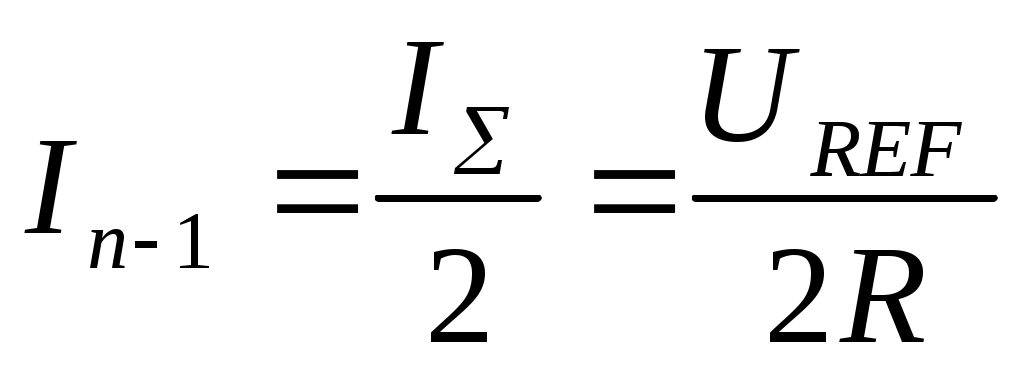(символом // обозначается параллельное соединение элементов). Входное сопротивление относительно узла b будет определяться из условия параллельного соединения сопротивления 2R и последовательно соединенных сопротивлений R и R_a: . Аналогично R_c=R и R_d=R. В результате имеем, что входное сопротивление всей матрицы равно R, а суммарный ток . Поскольку сопротивления цепей матрицы, подключенных к соответствующим узлам a, b, c, d одинаковые, то ток на выходе из очередного узла будет разделяться на две одинаковые составляющие I_i и I_i:

;

;

………………..

;

.

Или в общем виде:

.

Поскольку при произвольном коде X не все токи I_i могут образовывать суммарный ток I’_, втекающий в цепь обратной связи ОУ, а только те, которые коммутируются транзисторами VT1_i под управлением соответствующих разрядов X_i двоичного кода, то в общем случае для I’_ можно записать: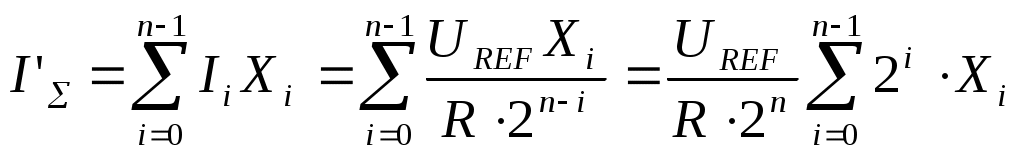

.

Выходное напряжение ОУ можно определить как:

.

Из полученной формулы видно, что U_вых ЦАП пропорционально входному двоичному коду и не зависит от сопротивления нагрузки. Можно отметить также, что сопротивления всего с двумя номиналами R и 2R относительно легко изготовить с хорошо согласованными характеристиками в едином технологическом процессе производства кристалла микросхемы ЦАП, что в значительной степени определяет точность ЦАП. Поскольку все ключи на транзисторах VT1_i и VT2_i также изготавливаются в едином технологическом процессе производства микросхемы ЦАП, то они имеют очень близкие параметры в режиме насыщения. Учитывая, что они используются для коммутации токов, задаваемых резисторами матрицы R-2R с одинаковыми значениями сопротивлений 2R, влияние этих ключей минимально. В выпускаемых промышленностью интегральных схемах ЦАП такие сопротивления изготавливаются из пленки поликремния, обладающего низким показателем температурного коэффициента сопротивления, с использованием в процессе изготовления лазерной подгонки. В условных графических обозначениях функция ЦАП определяется комбинацией символов «D/A» или «#/», а в маркировке микросхем – комбинацией символов «ПА».
10.3. Аналого-цифровые преобразователи.

Аналого-цифровые преобразователи.

Именно в АЦП реализуется принцип измерения, т.е. осуществляется сравнение неизвестной величины с некоторыми заданными нормированными мерами. Поскольку входная неизвестная (измеряемая) величина АЦП представлена в аналоговой форме, а значения нормированных мер (промежуточные выходные коды АЦП) формируются в цифровом виде, то для возможности их сравнения аналоговым компаратором последние должны также представляться и в аналоговой форме. По этой причине большинство типов АЦП содержат в своей структуре ЦАП. Исключения составляют лишь некоторые АЦП, в которых меры изначально представлены в аналоговой форме. Рассмотрим различные типовые методы и схемы АЦП.

10.3.1. АЦП последовательного счета.

АЦП последователного счета осуществляют сравнение входной аналоговой величины с суммой значений нескольких одинаковых мер. Момент равенства этих величин фиксируется безгистерезисным компаратором. Схема одного из вариантов такого АЦП, получившего название развертывающего или циклического, представлена на рис. 10.5,а. На вход компаратора DA1 поступают два аналоговых сигнала – входное напряжение U_вх схемы и выходное напряжение U_{вых.ЦАП} с ЦАП DА2 в виде нормированных квантованных уровней. Компаратор устанавливает соотношение мгновенных амплитуд этих напряжений. Если U_вх>U_{вых.ЦАП}, на выходе компаратора устанавливается уровень напряжения логической единицы, если U_вхU_{вых.ЦАП}, то на выходе компаратора устанавливается напряжение логического нуля. Единичный уровень сигнала с выхода компаратора, поступая на вход вентиля И DD1, разрешает передачу на счетный вход счетчика DD2 тактовых импульсов с генератора GN. В противном случае, если на выходе компаратора логический нуль, счетные импульсы на вход счетчика не проходят. Таким образом, подсчет импульсов осуществляется только при условии U_вх>U_{вых.ЦАП}.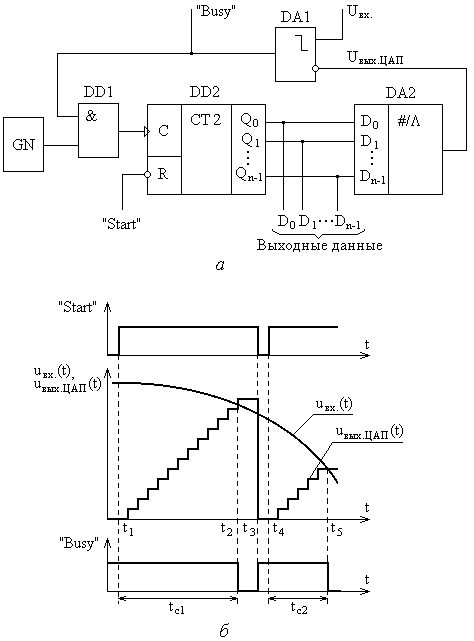



Рис. 10.5. Схема (а) и временная диаграмма работы (б) развертывающего АЦП.

В исходном состоянии на входе «Start» схемы присутствует уровень логического нуля (рис.10.5,б). Данный уровень является активным для входа R установки счетчика в нулевое состояние. В результате нулевой двоичный код с выхода счетчика поступает на вход ЦАП, на выходе которого устанавливается нулевое напряжение U_{вых.ЦАП}. Если входное напряжение U_вх схемы больше нуля, то выполняется условие U_вх>U_{вых.ЦАП} и счетные импульсы проходят на вход счетчика. При этом счетчик удерживается в нулевом состоянии нулевым значением сигнала «Start». Для запуска преобразования в момент времени t₁ на вход «Start» подается уровень логической единицы. Начинается подсчет импульсов с тактового генератора. С каждым текущим импульсом на выходе ЦАП будет формироваться потенциал следующего квантованного уровня. Как только выходное напряжение ЦАП достигнет или превысит амплитуду входного аналогового сигнала схемы, т.е. выполнится условие U_вхU_{вых.ЦАП}, компаратор переключится в нулевое состояние, элемент И закроется и подсчет тактовых импульсов прекратится. На выходе счетчика зафиксируется выходной код, соответствующий величине U_вх. На временной диаграмме этому соответствует момент времени t₂. Время преобразования t_c1=t₂-t₁.

Для приведения АЦП в исходное состояние необходимо счетчик DD2 нулевым сигналом «Start» сбросить в нуль (момент времени t₃). На выходе ЦАП сформируется нулевое выходное напряжение, выполнится условие U_вх>U_{вых.ЦАП}, но под действием нулевого уровня сигнала «Start» на выходе счетчика будет сохраняться нулевой двоичный код. Для запуска следующего преобразования на вход «Start» необходимо снова подать уровень логической единицы (момент времени t₄). Процесс преобразования повторится. Как только в очередной раз выполнится условие U_вхU_{вых.ЦАП} (момент времени t₅), преобразование завершится. Время преобразования в этом случае t_c2=t₅-t₄.

Из временной диаграммы очевидно, что время преобразования t_c1 и t_c2 различно и зависит от частоты следования тактирующих импульсов и формы входного аналогового сигнала. Поэтому для синхронизации работы АЦП с другими устройствами выход компаратора используется еще и как управляющий сигнал «Busy». Этот сигнал является признаком завершения преобразования. Пока сигнал «Busy» имеет единичный уровень, АЦП выполняет преобразование, на выходах D₀…D_n-1 присутствуют промежуточные некорректные коды. Считывание информации с этих выходов следует производить только после того, как сигнал «Busy» примет нулевое значение, т.е. после завершения преобразования.

Недостаток развертывающего АЦП заключается в его низком быстродействии, поскольку в процессе каждого преобразования суммирование нормированных мер начинается с нулевого значения. Этого недостатка лишены следящие или нециклические АЦП. Принцип их работы основан на том, что суммирование мер с нулевого значения осуществляется только при первом преобразовании. В дальнейшем следящий АЦП лишь корректирует выходной код в зависимости от входного аналогового сигнала. Схема следящего АЦП приведена на рис. 10.6,а.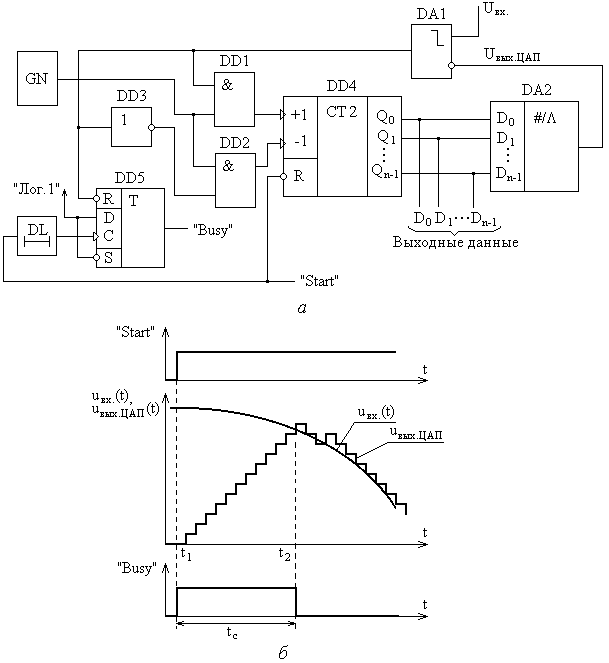



Рис. 10.6. Схема (а) и временная диаграмма работы (б) следящего АЦП.

Особенностью схемы является использование реверсивного счетчика DD4. Счетные импульсы на вход счетчика подаются через ключевые вентили И DD1 и DD2. Если выполняется условие U_вх>U_{вых.ЦАП}, то единичным сигналом с выхода компаратора элемент DD1 пропускает счетные импульсы на вход «+1» счетчика. На вход элемента DD2 в этом случае через инвертор DD3 подается логический ноль, в результате чего на выходе DD2 также формируется логический ноль, который подается на вход «-1» счетчика. Счетчик осуществляет положительный счет. Если же выполняется условие U_вхU_{вых.ЦАП}, то закрывается элемент DD1, инвертором DD3 открывается элемент DD2, через который счетные импульсы подаются на вход «-1» счетчика, и счетчик начинает выполнять операцию отрицательного счета.

Пока на входе «Start» присутствует нулевой уровень сигнала, также как и в случае с развертывающим АЦП, на выходе ЦАП DA2 удерживается нулевой потенциал (рис.10.6,б). При этом выполняется условие U_вх>U_{вых.ЦАП} и счетные импульсы подаются на вход «+1» счетчика. Как только на вход «Start» поступает логическая единица, разрешается положительный счет (момент времени t₁). Счет будет продолжаться до тех пор, пока выходное напряжение с ЦАП, пропорциональное коду подсчитанных импульсов, не достигнет значения амплитуды входного аналогового сигнала (момент времени t₂). При этом выполнится условие U_вхU_{вых.ЦАП} и счетчик начнет операцию отрицательного счета. Отрицательный счет будет продолжаться, пока вновь не выполнится условие U_вх>U_{вых.ЦАП} и счетчик не вернется к положительному счету. Таким образом, схема АЦП будет постоянно отслеживать амплитуду входного аналогового сигнала и пропорционально ей формировать выходной код D₀…D_n-1.

Врем преобразования t_c=t₂-t₁ обусловлено процессом только самого первого развертывающего преобразования и зависит от амплитуды входного сигнала. Для возможности синхронизации с другими устройствами в схеме следящего АЦП также предусмотрен управляющий сигнал «Busy». Сигнал с выхода компаратора в зависимости от направления счета постоянно будет менять свое значение с единицы на ноль. Для фиксации момента окончания первого следящего преобразования (момент времени t₂) в виде нулевого значения сигнала «Busy» и удержания его в дальнейшем в схеме АЦП предусмотрен D-триггер DD5 с динамическим управлением и статическими входами асинхронной установки в ноль и единицу. Для формирования единичного уровня сигнала «Busy» в момент начала преобразования в D-триггер по переднему фронту сигнала «Start» записывается логическая единица с входа D. Эта единица будет сохраняться до тех пор, пока на выходе компаратора не сформируется нулевой потенциал, являющийся признаком завершения первого развертывающего преобразования. Этот ноль поступит на инверсный асинхронный вход сброса триггера и установит его в нулевое состояние. На выходе триггера сформируется нулевой уровень сигнала «Busy». В дальнейшем это состояние триггера будет оставаться неизменным по причине отсутствия каких-либо воздействий, устанавливающих его в единичное состояние. Таким образом, сигнал «Busy» будет выполнять функцию признака завершения первого развертывающего преобразования.

Если счетчик находится в режиме отрицательного счета, то на входе D-триггера будет присутсвовать активный нулевой потенциал. Если теперь подать на вход «Start» нулевое значение сигнала для приведения схемы АЦП в исходное состояние, этот нулевой сигнал сброса с входа D-триггера снимется с некоторой задержкой, обусловленной временем срабатывания элементов (в порядке очередности их срабатывания) DD4, DA2 и DA1. Поэтому сигнал «Start» на динамический вход C D-триггера для установки на его выходе сигнала «Busy» необходимо подавать после того, как будет снят логический ноль со статического входа этого триггера, т.е. с некоторой задержкой. Для этих целей служит схема задержки DL, реализовать которую можно на интегрирующей RC-цепи с постоянной времени, равной суммарному времени задержки указанных выше элементов.

Важно отметить, что скорость изменения входного аналогового сигнала, подаваемого на следящий АЦП, не должна превышать некоторого предельного значения, обусловленного быстродействием АЦП и частотой следования тактовых импульсов с выхода генератора GN. В противном случае АЦП не будет успевать отслеживать изменение входного сигнала.

10.3.2. Интегрирующие АЦП.

В основу метода интегрирующего преобразования положен принцип сравнения значений интегралов амплитуд входного аналогового сигнала u_вх(t) в определенных пределах и опорного напряжения U_REF в тех пределах, при которых разница этих двух интегралов дает нулевой результат. Нахождение каждого такого интеграла реализуется за один такт преобразования, т.е. за два такта в сумме для обоих интегралов. Поэтому такой метод преобразования часто называют методом двухтактного интегрирования. В качестве результата аналого-цифрового преобразования принимается двоичный код X, пропорциональный пределам интегрирования опорного напряжения. Математически это можно записать: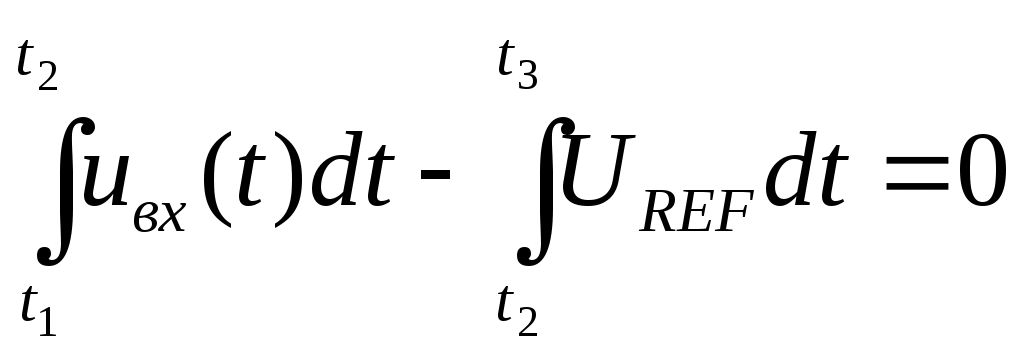



.

Двоичный код может быть получен путем заполнения интервала t_инт тактовыми импульсами и подсчета их двоичным счетчиком. Для определенности пределов интегрирования такими же импульсами заполняется и интервал времени t₂-t₁. Этот интервал должен быть одинаковым при каждом преобразовании и обычно выбирается соответствующим модулю счета K_сч используемого двоичного счетчика.

Вариант схемы АЦП с двухтактным интегрированием представлена на рис. 10.7,а. Можно отметить отсутствие в приведенной схеме ЦАП, поскольку обе сравниваемые величины u_вх(t) и U_REF представлены в аналоговой форме. Компаратор DA3 выполнен так, что когда выходное напряжение с интегратора, реализованного на операционном усилителе DA2, резисторе R и конденсаторе C, равно нулю, т.е. когда U_вых.DA2=0, то на его выходе устанавливается уровень логического нуля. Если выходное напряжение интегратора меньше нуля U_вых.DA2<0, то на выходе компаратора устанавливается логическая единица.

В исходном состоянии триггеры DD1 и DD2 сброшены в ноль и ключи SW1 и SW2 разомкнуты. На выходе вентиля ИЛИ DD4 формируется ноль, который инвертируется в единицу инвертором DD5, замыкая тем самым ключ SW3. Это обеспечивает нулевое начальное напряжение на конденсаторе C и нулевое напряжение на выходе интегратора. Выполняется условие U_вых.DA2=0, на выходе компаратора формируется нулевой логический уровень, который закрывает стробирующий вентиль И DD6, в результате чего импульсы с выхода генератора GN на счетчик DD2 на проходят. Преобразование начинается с подачи на вход «Start» схемы короткого единичного импульса (момент времени t₁) (рис.10.7,б). По этому импульсу триггер DD1 устанавливается в единицу и замыкается ключ SW2. На выходе вентиля ИЛИ DD4 также формируется единица, которая инвертируется инвертором DD5 в ноль и размыкается ключ SW3. В результате на вход интегратора подается амплитуда входного напряжения. Если изменение входного напряжения u_вх(t) отсутствует или происходит со временем, значительно превышающим постоянную времени =RC, то можно считать входное напряжения постоянным в масштабе периода интегрирования. В этом случае на выходе интегратора напряжение начинает линейно убывать. Выполняется условие U_вых.DA2<0, на выходе компаратора формируется логическая единица, которая открывает элемент И DD6. Тактовые импульсы с выхода генератора GN начинают поступать на счетчик DD7.

После того, как будут подсчитаны К_сч импульсов, на выходе счетчика сформируется единичный уровень сигнала переноса P, который сбросит триггер DD1 в ноль и установит триггер DD2 в еднинцу. В результате ключ SW2 закроется, а SW1 откроется (момент времени t₂). На выходе вентиля ИЛИ DD4 будет сохраняться единица, на выходе инвертора DD5 - ноль, и ключ SW3 будет оставаться размкнутым. Напряжение на выходе интегратора в момент времени t₂ определяется из формулы: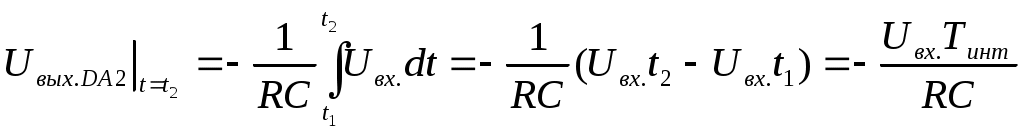

.

Поскольку интегрирование входного напряжения прекращается сигналом переноса P счетчика, то время интегрирования Т_инт получается постоянным, независящим от амплитуды входного напряжения, а зависящим только от частоты следования тактовых импульсов и К_сч счетчика.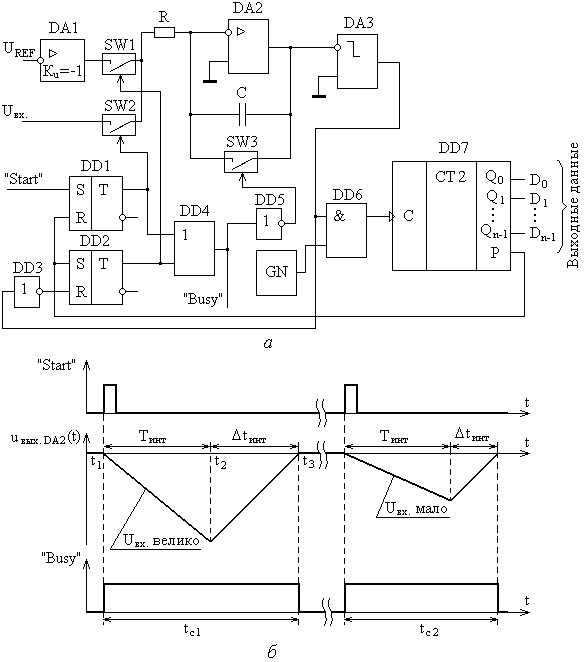



Рис. 10.7. Схема (а) и временная диаграмма работы (б) двухтактного интегрирующего АЦП.

С открытием ключа SW1 на вход схемы начинает подаваться опорное напряжение U_REF через аналоговый инвертор DA1, т.е. на вход интегратора оно поступает с отрицательной полярностью. Напряжение U_REF можно формировать изначально отрицательной полярности, тогда необходимость в инверторе DA1 отпадет. Напряжение на выходе интегратора не может измениться скачком, поэтому оно начинает линейно возрастать. В момент времени t₃ оно достигнет нулевого уровня U_вых.DA2=0, на выходе компаратора DA3 сформируется уровень логического нуля, который закроет элемент И DD6, подача счетных импульсов на счетчик прекратится. Одновременно через инвертор DD3 сбросится в ноль триггер DD2 и закроется ключ SW1. На выходах обоих триггеров будут присутствовать нули, которые поступят на входы вентиля ИЛИ DD4, в результате чего на его выходе сформируется ноль. Этот ноль проинвертируется инвертором DD5 и откроется ключ SW3 для разряда конденсатора и приведения его в исходное состояние. На выходе счетчика зафиксируется двоичный код, пропорциональный входному напряжению. Для выходного напряжения интегратора в момент времени t₃ можно записать: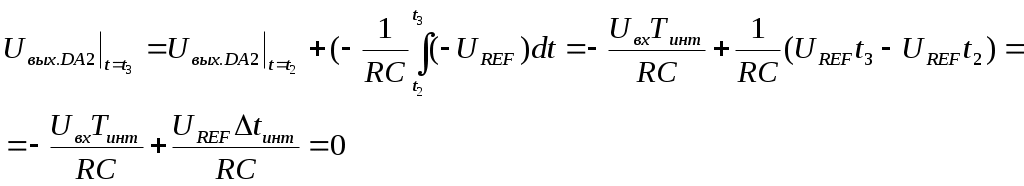



или



откуда

.

Таким образом, количество подсчитанных двоичным счетчиком тактовых импульсов в период и сформированный цифровой код Х прямо пропорционален входному аналоговому напряжению. Для облегчения синхронизации работы с другими устройствами в схеме рассмотренного АЦП также предусмотрен управляющий выходной сигнал «Busy». Поскольку весь процесс двухтактного преобразования сопровождается логическим нулем на выходе вентиля ИЛИ DD4, его выход можно использовать и как цепь сигнала «Busy».

Ключ SW2 коммутирует только положительный потенциал входного напряжения U_вх. Поэтому его можно реализовать на основе n-канального полевого транзистора с индуцированным каналом, как это делалось в схемах ЦАП. Ключи SW1 и SW3 коммутируют отрицательные потенциалы (-U_REF и -U_вых.DA2). Для реализации этих ключей необходимо использовать аналогичные транзисторы, но с каналом p-типа. Для управления такими транзисторами на их затворы необходимо подавать сигналы логических единиц с отрицательными потенциалами. Для формирования отрицательных уровней напряжения в схеме можно использовать двуполярный источник питания и инверторы полярности напряжений.

АЦП двухтактного интегрирования, также как и АЦП последовательного счета, обладает не высоким быстродействием, поскольку выходной код формируется процессом подсчета тактовых импульсов, длительность которого зависит от амплитуды входного аналогового сигнала. Часто интегрирующие АЦП по этой причине относят к АЦП последовательного счета. Между тем двухтактный интегрирующий АЦП обладает существенным достоинством. По причине интегрирования входного сигнала осуществляется фильтрация высокочастотных помех. Кроме того, период интегрирования T_инт входного напряжения можно выбрать таким, чтобы почти полностью исключить помехи с частотами, кратными 1/T_инт. Для исключения помех, вызванных наводками бытовой сети с частотой 50 Гц, период интегрирования должен выбираться кратным значению 1/50 с. Отсюда следует, что интегрирующие АЦП целесообразно применять для оцифровки аналоговых сигналов, характеризующихся сверхнизкими частотами.

10.3.3. АЦП последовательного приближения.

В основе метода последовательного приближения или, как его еще называют, поразрядного уравновешивания лежит принцип сравнения амплитуды входного аналогового сигнала с сумой различных по значению мер. Число таких мер равно числу разрядов АЦП, а их значения пропорциональны отдельным разрядам двоичного кода. Мера с самым большим значением напряжения соответствует старшему разряду кода, а с самым малым – младшему. Причем значение каждой следующей меры вдвое меньше значения предыдущей. Сумма значений всех мер соответствует величине максимального входного напряжения АЦП. Просуммировав только те меры, общее значение которых совпадет с напряжением входного сигнала, на выходе АЦП установится соответствующий этим значениям двоичный код. В этом плане метод поразрядного уравновешивания очень напоминает процесс взвешивания на коромысельных весах путем их уравновешивания необходимым количеством гирь. Схема АЦП последовательного приближения приведена на рис. 10.8,а.

Элементы DD2…DD4 образуют так называемый регистр последовательных приближений. Преобразование начинается с выставления короткого единичного импульса на входе «Start» (момент времени t₁ рис.10.8,б). По этому сигналу осуществляется установка в единичное состояние RS-триггера DD4.0 самого старшего разряда D_n-1 выходного кода. Триггеры DD4.1…DD4.n-1 остальных разрядов D_n-2…D₀ через элементы ИЛИ DD3.1…DD3.n-1 сбрасываются в нулевое состояние. Таким образом, на входе ЦАП DА2 фиксируется код с единицей в самом старшем разряде и нулями в остальных разрядах. Передним фронтом импульса тактового генератора GN единичный уровень сигнала «Start» записывается в младший разряд Q₀ последовательного регистра DD1, который в свою очередь открывает вентиль И DD2.0. Если значение выходного напряжения с ЦАП превышает или равняется амплитуде входного сигнала, т.е. выполняется условие U_{вых.ЦАП}U_вх, то на выходе компаратора DA1 формируется логическая единица, которая проходит через открытый вентиль И DD2.0 на вход сброса R триггера DD4.0 и устанавливает его в нулевое состояние. В самом старшем разряде выходного кода формируется логический ноль. Если выходное напряжение с ЦАП оказывается меньше амплитуды входного сигнала, т.е. выполняется U_{вых.ЦАП}<U_вх, то на выходе компаратора формируется логический ноль, элемент DD2.0 закрывается и триггер DD4.0 сохраняет единичное состояние.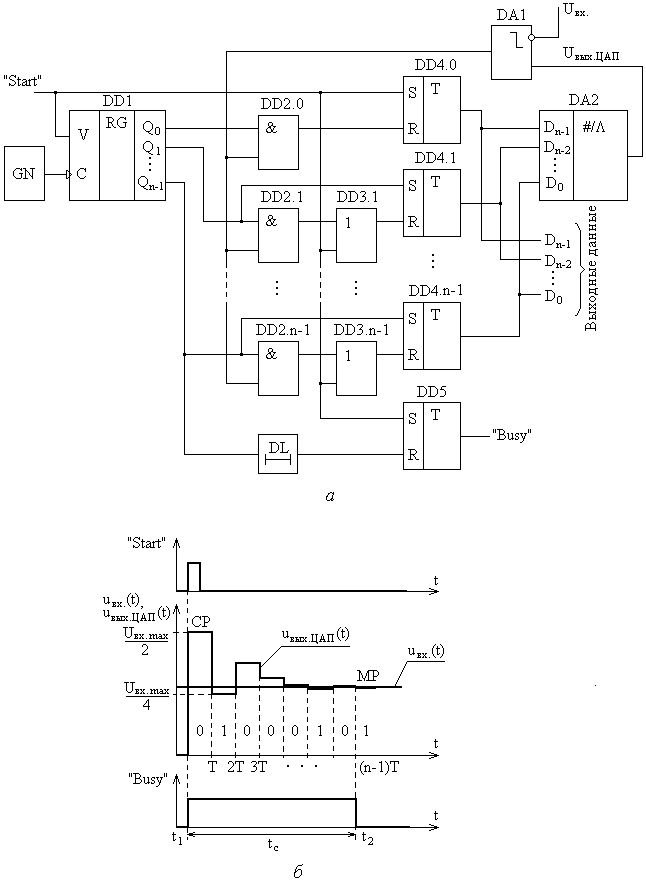



Рис. 10.8. Схема (а) и временная диаграмма работы (б) АЦП последовательного приближения.

Вторым тактовым импульсом осуществляется сдвиг единицы в регистре из разряда Q₀ в разряд Q₁. Сигнал «Start» при этом должен быть сброшен в ноль. Тогда в разряде Q₀ регистра формируется логический ноль. Элемент DD2.0 закрывается, а элемент DD2.1 открывается. Триггер DD4.0 оказывается лишенным каких-либо воздействий и сохраняет сформированное значение старшего разряда двоичного кода. Логическая единица с выхода Q₁ регистра подается на вход установки S триггера DD4.1 и устанавливает его в единичное состояние. На входе ЦАП формируется новый код с сохраненным значением старшего разряда D_n-1 и установленным единичным значением разряда D_n-2. Новое сформированное напряжение с выхода ЦАП поступает на компаратор. При этом, если выполняется условие U_{вых.ЦАП}U_вх, то на выходе компаратора вновь формируется логическая единица, которая проходит через элементы DD2.1 и DD3.1 и сбрасывает триггер DD4.1 в нулевое состояние. Если U_{вых.ЦАП}<U_вх, компаратор формирует напряжение логического нуля и триггер сохраняет установленное единичное состояние. Таким образом, триггер DD4.1 фиксирует значение разряда D_n-2. Процесс будет продолжаться в сторону убывания разрядов D_i до тех пор, пока не сформируются значения всех разрядов выходного двоичного кода (момент времени t₂).

Очевидно, что время преобразования t_c=t₂-t₁ определяется только частотой следования импульсов тактового генератора и количеством разрядов выходного кода. При этом от формы входного аналогового сигнала это время не зависит, т.е. оно постоянно. Поэтому для определения момента завершения преобразования можно просто воспользоваться техническими характеристиками АЦП. Тем не менее, для облегчения синхронизации работы АЦП с другими устройствами предусмотрен выходной управляющий сигнал «Busy», формируемый триггером DD5. Для установки этого сигнала в единичное состояние импульсом «Start» в момент запуска преобразования триггер DD5 устанавливается в единицу. По последнему n-му тактовому импульсу единица сдвинется на выход Q_n-1 регистра DD1 и начнется процесс формирования значения последнего младшего разряда двоичного кода. Поскольку для завершения этого процесса требуется некоторый фиксированный промежуток времени, логическую единицу с выхода Q_n-1 регистра на вход R триггера DD5 необходимо подать через элемент задержки DL с соответствующей величиной времени задержки. Это приведет к формированию нулевого уровня сигнала «Busy», являющегося признаком завершения преобразования.

10.3.4. АЦП параллельного действия.

В основе метода параллельного действия лежит принцип одновременного сравнения входного напряжения со всеми квантованными уровнями. Для реализации такого принципа преобразования АЦП в своей структуре должен содержать 2ⁿ компараторов, где n – количество разрядов выходного двоичного кода (рис. 10.9). Каждый j-й компаратор DA1.j срабатывает при j-ом квантованном уровне. Самый первый компаратор DA1.1 имеет в качестве порогового напряжения квантованный уровень Q, второй компаратор DA1.2 – квантованный уровень Q+Q=2Q и т.д. Пороговые уровни задаются резистивным делителем, состоящим из 2ⁿ⁺¹ одинаковых резисторов R, делящим опорное напряжение U_REF на m=2ⁿ равных значений. Если на входе j-ого компаратора амплитуда входного аналогового сигнала U_вх превышает текущий квантованный уровень, то на его выходе формируется логическая единица. В противном случае на выходе этого компаратора формируется логический ноль. Сигналы с выходов всех компараторов поступают на вход быстродействующего двоичного шифратора DD1. На выходе этого шифратора формируется двоичный код, соответствующий максимальному номеру входа, на который поступает логическая единица с выхода соответствующего компаратора.

Так как все компараторы срабатывают одновременно, то преобразование осуществляется за один такт. Преимущество параллельного АЦП заключается в его максимальном быстродействии по сравнению с АЦП других типов. Максимальная частота f_c.max преобразования таких АЦП может достигать сотен МГц, что делает их незаменимыми в радиотехнике. Между тем очевиден недостаток параллельных АЦП – слишком сложная аппаратная реализация, связанная с большим количеством компараторов и резисторов делителя, геометрически возрастающим с увеличением разрядности выходного кода. Поэтому, параллельные АЦП имеют обычно не высокую разрядность выходного кода.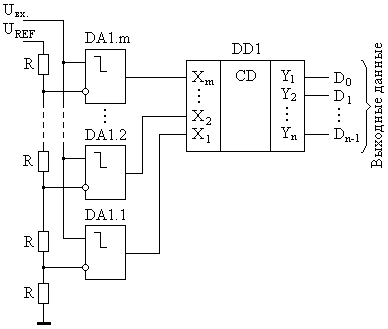



Рис. 10.9. Схема параллельного АЦП.

В заключение можно отметить, что функция АЦП в условных графических обозначениях задается комбинациями символов «D/A» или «/#», а в маркировке микросхем – символами «ПВ». В последнее время широкое распространение получили АЦП и ЦАП с последовательной передачей выходного и входного кодов соответственно. Это означает, что передаваемый из преобразователя или в преобразователь двоичный код представляется не в параллельном, а в последовательном виде. Примерами подобных интерфейсов могут служить интерфейсы стандартов SPI и I²C. Протоколы этих интерефейсав будут рассмотрены в главе 12. Сейчас только отметим, что все разряды двоичного кода при последовательном протоколе обмена передаются поочередно путем их сдвига аналогично записи в последовательный регистр. Такая организация интерфейса обмена данными позволяет сократить число выводов микросхемы преобразователя. Например, существуют микросхемы 10-, 12-, и 16-разрядных АЦП и ЦАП всего с восемью выводами, включая выводы питания и управляющие. В структуре таких преобразователей присутствуют регистры сдвига, заполняемые или считываемые с помощью специальных синхронизирующих передачу импульсов «Clock». Разумеется, что такая организация обмена данными может снижать производительность с позиции скорости передачи и усложнять схему организации связи микросхемы АЦП/ЦАП с прочими устройствами. Но во многих случаях последовательная передача является преимущественной из-за малого количества внешних выводов микросхемы и, как следствие, малого размера микросхемы. Преобразователи с последовательной передачей кода широко используются при обработке сигналов в диапазоне звуковых частот, т.е. не превышающих десятки кГц.
Контрольные вопросы

1. 
   Какие методы дискретизации аналоговых сигналов Вам известны?
   
2. 
   Какие характеристика АЦП и ЦАП определяют их точность?
   
3. 
   Какими недостатками обладает структура ЦАП со взвешенными резисторами?
   
4. 
   Опишите принцип функционирования ЦАП с резисторной матрицей R-2R.
   
5. 
   Сформулируйте принцип аналого-цифрового преобразования методом последовательного счета.
   
6. 
   Почему следящие АЦП обладают более высоким быстродействием по сравнению с АЦП развертывающего преобразования?
   
7. 
   Опишите работу АЦП двухтактного интегрирования. Какие элементы необходимо заменить в схеме для реализации АЦП двухтактного интегрирования с большей разрядностью выходного кода?
   
8. 
   АЦП каких типов следует выбрать при оцифровке аналоговых сигналов с частотами в диапазоне сотен МГц и в диапазоне единиц Гц?
   
9. 
   Каким преимуществом и недостатком обладает последовательный канал передачи двоичного кода в ЦАП или из АЦП?