Курс лекций. Теория статистики Пособие для студентов, обучающихся по дистанционной системе Введение Статистика
 Скачать 2.79 Mb.
|
Сводка и группировка статистических данных 3.3. Ряды распределения: виды, правила построения и графическое отображение Результаты группировки можно представить в виде статистических рядов распределения. Ряд распределения – это упорядоченное распределение единиц совокупности на группы по изучаемому признаку. В зависимости от группировочного признака различают атрибутивные и вариационные ряды. Атрибутивными рядами распределения называют ряды, построенные по качественным признакам. Примером атрибутивных рядов являются распределения населения по полу, национальности, статусу занятости, образованию и т.д. Вариационными рядами распределения называют ряды, построенные по количественным признакам. Например, распределение населения по возрасту, сотрудников по стажу работы и уровню заработной платы, домохозяйств – по уровню доходов и расходов и т.д. Вариационный ряд состоит из двух элементов: вариантов и частот. Под вариантами понимают конкретные значения признака, которые он принимает в вариационном ряду. Частоты (  )– это численности отдельных вариантов или каждой группы вариационного ряда, то есть это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Накопленные частоты ( ) показывают число единиц совокупности, у которых значение варианта не больше данного. Сумма всех частот называется объемом совокупности( ). Помимо частот в вариационном ряду распределения могут рассчитываться частости( ), представляющие собой частоты, выраженные либо в долях единицы, либо в процентах относительно объема совокупности ( ). Накопленные частости ( ) рассчитываются как отношение накопленной частоты к числу единиц совокупности и характеризуют долю единиц совокупности со значением не больше данного варианта. В зависимости от характера вариации вариационные ряды подразделяются на дискретные и непрерывные. Дискретный вариационный рядхарактеризует распределение единиц совокупности по дискретному признаку, то есть признаку, принимающему только дискретные значения, число которых составляет счетное множество. Например, дискретный вариационный ряд может быть построен в случае группировки домохозяйств по числу детей, работающих членов семьи, иждивенцев. Пример 3.1.Имеются следующие данные о количестве детей в 60 семьях:
Решение. Для того чтобы построить вариационный ряд, ранжируем (упорядочим) исходные данные:
Затем подсчитаем число семей, в которых вариационный признак (  ) – количество детей, имеет одинаковое значение, то есть найдем частоту ( ) и оформим результаты подсчетов в виде ряда распределения, записанного в таблице:
Это - дискретный вариационный ряд, так как значения признака могут принимать конечное число отдельных значений. В случае непрерывной вариации, когда величина варьирующего признака может принимать в определенных пределах любые значения, отличающиеся друг от друга на сколь угодно малую величину, целесообразно строить интервальные вариационные ряды. Значения вариант в интервальных вариационных рядах могут быть как дробными, так и целыми. Значения варьирующего признака в этом случае задаются в виде интервалов. Каждый интервал имеет нижнюю границу (наименьшее значение признака в интервале) и верхнюю границу (наибольшее значение признака в интервале). Величина интервала представляет собой разность между его верхней и нижней границами. Если интервал имеет обе границы, его называют закрытым. Первый и последний интервалы могут быть открытыми. В этом случае, первый интервал не имеет нижней границы, а последний верхней. Такие интервалы могут быть условно закрыты. Для этого предполагается, что величина первого интервала равна величине второго, а величина последнего равна величине предпоследнего интервала. Далее от верхней границы первого интервала отнимают величину второго интервала и получают нижнюю границу первого интервала, а к нижней границе последнего интервала прибавляют величину предпоследнего и получают верхнюю границу последнего интервала. Интервальные вариационные ряды могут также строится на основе дискретных рядов в случае, когда значительное число вариантов дискретного ряда имеют небольшую частоту появления относительно всего объема совокупности. При построении интервального вариационного ряда важно определить величину интервала. Для этого используют формулу Стерджесса:
где  - минимальное значение признака в совокупности,  - максимальное значение признака в совокупности,N - объем совокупности. Для уточнения представления об интервальных вариационных рядах рассчитывают абсолютные и относительные плотности.Абсолютная плотность распределения - это частота, приходящаяся на единицу длины интервала. Абсолютная плотность интервала рассчитывается по формуле:
Относительная плотность распределения – частость, приходящаяся на единицу длины интервала. Относительная плотность интервала может быть рассчитана как:
Пример 3.2В результате статистического опроса получены данные о заработной плате 30 специалистов коммерческих банков (тыс. руб.):
Решение. Сделать какие-либо выводы из исходных данных не представляется возможным. Строить дискретный вариационный ряд также нерационально, так как он будет иметь большое число значений с частотами равными единице. Более правильно построить интервальный вариационный ряд. Для этого воспользуемся формулой Стерджесса и определим величину интервала  При расчете величины интервала целесообразно округлять знаменатель до целого. В противном случае, при построении интервального ряда верхняя граница последнего интервала может не соответствовать максимальному значению признака в исходной совокупности. Учитывая, что минимальное значение признака 17, образуем первый интервал, прибавив к минимальному значению величину интервала 10, то есть нижняя граница первого интервала 17, а верхняя 27, второй интервал соответственно 27-37 и т.д. Таким образом, получим интервалы 17-27, 27-37, 37-47, 47-57, 57-67, 67-77. Ранжируем исходные данные:
Подсчитаем частоты. При подсчете возникает ситуация, в которой вариант (например 27) попадает на границу интервалов и может быть отнесен как к более раннему интервалу, так и к следующему за ним. В этом случае следует отнести его к интервалу, на верней границе которого он находится. Таким образом, 27 относится к первому интервалу. Результаты построения интервального вариационного ряда запишем в виде таблицы: Распределение специалистов коммерческих банков по величине заработной платы
Вариационный ряд можно изобразить графически. Дискретный вариационный ряд можно изобразить в виде полигона распределения. Полигон распределения строится в прямоугольной системе координат, при этом, на оси абсцисс откладывают значения вариант, а на оси ординат частоты или частости. Полученные точки соединяют отрезками, в результате чего получается ломаная линия, которая и будет полигоном распределения. Построим полигон распределения по данным примера 3.2. 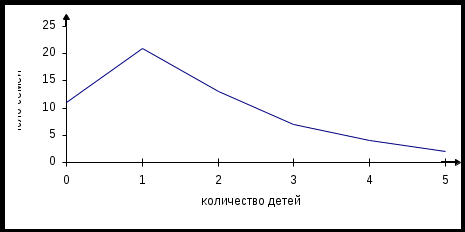 Рис.3.1. Полигон распределения Интервальный вариационный ряд можно изобразить в виде гистограммы распределения. Для интервального ряда с равнымиинтервалами на оси абсцисс откладывают отрезки равные длине интервала. На основании этих отрезков строят прямоугольники, высота которых пропорциональна частотам или частостям соответствующих интервалов. Нижеприведенная гистограмма распределения построена по данным примера 3.3.    Рис. 3.2. Гистограмма распределения Для интервального ряда с неравными интервалами на оси ординат откладывают плотности распределения. Дискретные и интервальные вариационные ряды можно представить в виде кумуляты и огивы. При построении кумуляты дискретного вариационного ряда на оси абсцисс откладывают значения признака (варианты), а по оси ординат – соответствующие им накопленные частоты (частости). Кумулята дискретного вариационного ряда представляет собой ступенчатую разрывную линию, имеющую конечные разрывы в точках, соответствующим значениям варианта. Для интервального вариационного ряда кумулята представляет собой ломанную, начинающуюся с точки, абсцисса которой равна началу первого интервала, а ордината – накопленной частоте (частости), равной нулю. Другие точки этой ломаной соответствуют концам интервалов. Огива строится аналогично кумуляте лишь с той разницей, что на оси абсцисс откладываются значения, соответствующие накопленным частотам (частостям), а на оси ординат – значения признака (варианты). |
