урок математики. Учебник для учащихся общеобразовательных учреждений в 2 ч. В. Н. Рудницкая, Т. В. Юдачева. М. ВентанаГраф, 2010
 Скачать 2.65 Mb. Скачать 2.65 Mb.
|
|
Многогранник Многогранником называется тело, ограниченное конечным числом плоскостей. Граница многогранника называется его поверхностью (рис. 2). 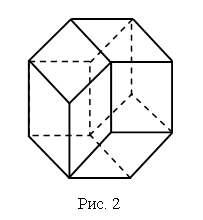 Многогранник называется выпуклым, если он лежит по одну сторону от каждой из ограничивающих плоскостей. Общая часть поверхности выпуклого многогранника и ограничивающей его плоскости называется гранью. Стороны граней многогранника называются ребрами, а вершины – вершинами многогранника. Поясним данное определение на примере знакомого вам куба (рис. 3). Куб есть выпуклый многогранник. Его поверхность состоит из шести квадратов: ABCD, BEFC, ... . Они являются его гранями. Ребрами куба являются стороны этих квадратов АВ, ВС, BE, ... . 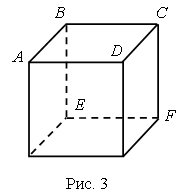 Вершинами куба являются вершины квадратов А, В, С, D, Е, ... . У куба шесть граней, двенадцать ребер и восемь вершин. Призма Призмой называется многогранник, образованный заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, которые пересекают плоский многоугольник в одной из плоскостей. Грани призмы, лежащие в этих плоскостях, называются основаниями призмы. Другие грани называются боковыми гранями. Все боковые грани – параллелограммы. Ребра призмы, соединяющие вершины оснований, называются боковыми ребрами. Все боковые ребра призмы параллельны. Высотой призмы называется расстояние между плоскостями ее оснований. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю призмы. Диагональным сечением призмы называется сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. Призма называется прямой, если все боковые грани составляют с основаниями прямые двугранные углы. Если основание призмы есть параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани – параллелограммы. На рисунке 4а изображен наклонный параллелепипед, а на рисунке 4б – прямой параллелепипед. 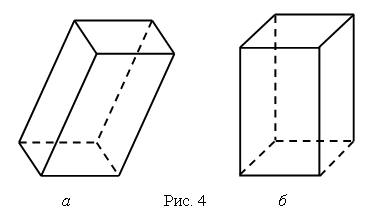 Правильные многогранники Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер. Существует пять типов правильных выпуклых многогранников (рис. 5): правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. 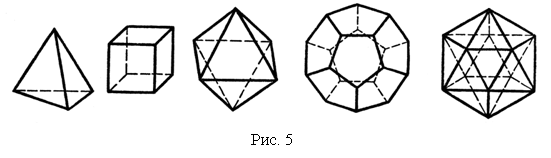 У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны. У куба все грани – квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными ребрами. У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра. У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра. У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер. Урок 4 Двузначные числа и их запись Цели урока: рассмотреть изображение двузначных чисел с помощью цветных палочек; закреплять навыки сложения и вычитания чисел в пределах 20; совершенствовать навык счёта в пределах 100; развивать логическое мышление и умение анализировать. Ход урока I. Организационный момент. II. Устный счёт. 1. Сколько всего отрезков на чертеже?  2. Являются ли эти квадраты «магическими»?
3. Решите задачу. Дети были на экскурсии в музее. На первом этаже они осмотрели 6 витрин, а на втором – на 5 витрин больше. Сколько витрин осмотрели дети на втором этаже? 4. Задание на смекалку. Таня разложила елочные шары в три одинаковые коробки. В одну коробку она положила красные шары, в другую – голубые, а в третью – и те, и другие. Заклеила, и когда стала их надписывать, то перепутала все коробки. Догадайтесь, какие шары лежат в каждой коробке, если в коробке с надписью «Красные шары» лежат голубые. 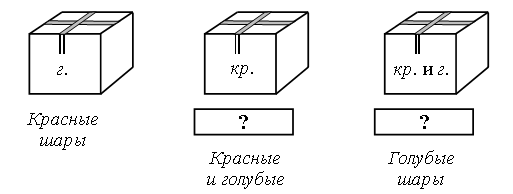 III. Сообщение темы урока. – Сегодня на уроке мы научимся записывать двузначные числа, количество единиц которых не равно нулю. IV. Знакомство с новым материалом. Задание № 1 (с. 11). – Рассмотрите рисунок на с. 11 учебника: Волк и Заяц собирают урожай гороха. – Сколько горошин в каждом стручке держит Волк? (Десять.) – А сколько у Волка стручков? (Два стручка, значит, два десятка горошин.) – Сколько горошин в стручке у Зайца? (Пять горошин, или пять единиц.) – Сколько всего горошин у Волка и Зайца? (2 десятка и 5 единиц.) – Прочитайте, что написано в учебнике. – С такими записями, как 2 д. 5 ед., мы еще не встречались. Сегодня мы научимся читать и записывать такие числа цифрами. – Прочитайте число 2 д. 5 ед. (два десятка пять единиц) по-другому: сначала назовите число, выраженное первой цифрой и буквой «д», получится «двадцать», а затем число, выраженное второй цифрой, получится «пять». Итак, число 2 д. 5 ед. читается так: «двадцать пять». А как его записать цифрами? – Посмотрите: на доске составлена запись этого числа с помощью карточек: 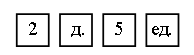 Сейчас я уберу буквы, а цифры придвину одна к другой. Получилась запись: 25. Записи «25» и «2 д. 5 ед.» являются разными обозначениями одного и того же числа – «двадцать пять». Если переставить цифры, то получится совсем другое число – «52» (пятьдесят два), в нем 5 десятков 2 единицы. Поэтому при записи двузначного числа его цифры располагают в строго определенном порядке: первая цифра слева – это десятки, а вторая – единицы. В числе «шестьдесят» содержится 6 десятков 0 единиц. Поэтому его записывают так: 60. Любое двузначное число можно изобразить с помощью цветных палочек. Возьмите из набора одну оранжевую палочку и положите ее перед собой. Поставьте на нее в ряд столько белых палочек, сколько поместится. Сколько белых палочек поместилось на одной оранжевой палочке? (Десять.) Давайте договоримся число десятков в числе обозначать оранжевыми палочками, а число единиц – белыми палочками. Палочки мы будем выкладывать вплотную одна к другой. – Посмотрите на рисунок в учебнике; скажите, как изображено число 25 с помощью палочек: сколько палочек каждого цвета? Объясните, почему понадобилось именно столько оранжевых и белых палочек. – Сколько и каких палочек надо взять, чтобы изобразить числа 16, 61, 40, 4? С какой стороны (слева или справа) вы будете выкладывать оранжевые палочки; белые палочки? Итак, запомним: изображая десятки, выкладываем оранжевые палочки слева; изображая единицы, выкладываем белые палочки слева (вслед за оранжевыми). Задание № 2 (с. 11). Учащиеся называют числа по порядку. а) 31, 32, 33, 34, 35, … , 50 (прямой счет); б) 80, 79, 78, 77, 76, 75, 74, 73, 72, 71, 70 (обратный счет). – Как составлен первый числовой ряд? Второй числовой ряд? Задание № 3 (с. 12). Задание очень важно с методической точки зрения. В ходе его выполнения дети учатся «выкладывать» числа с помощью цветных палочек, а это умение – одно из ключевых при изучении письменных приемов сложения и вычитания натуральных чисел в пределах 100. Рассмотрим на примере случая 1, как учащиеся должны рассуждать. Прочитав фразу, они прежде всего называют числа, которые встретились в этом предложении (три, тринадцать и тридцать один). Затем последовательно «выкладываем» каждое число. В числе «три» – три единицы, значит, для «выкладывания» этого числа нужны три белые палочки:
В числе «тринадцать» – один десяток и три единицы, значит, потребуется одна оранжевая палочка и три белые. Сначала кладем оранжевую палочку, а затем белые:
В числе «тридцать один» – три десятка и одна единица, значит, «выложить» это число можно так:
Аналогично ученики рассуждают и при рассмотрении случая 2.  V. Повторение пройденного материала. 1. Работа с учебником. Задание № 11 (с. 13). Учащиеся выполняют вычисления, используя знание таблицы сложения и вычитания чисел в пределах 20. Задание № 12 (с. 13). – Какое арифметическое действие необходимо выполнить при нахождении значения суммы чисел? – А какое при нахождении значения разности чисел? – Значение суммы каких чисел будет равно значению разности этих чисел? (12 + 0 = 12 – 0.) – Объясните почему. 2. Работа в печатной тетради № 1. Задание № 7. Учитель должен обратить внимание учащихся на предложенные образцы. Запись:
Задание № 8. Учащиеся работают самостоятельно. Взаимопроверка в парах. 3. Работа по карточкам. Задание № 1. Разгадайте правило, по которому составлены схемы, и вставьте пропущенные числа. 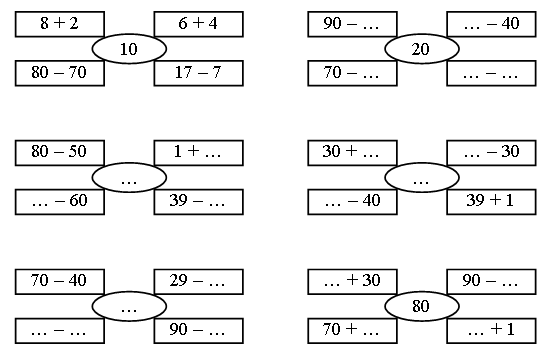 Задание № 2. Вставьте пропущенные знаки действий, чтобы получились верные равенства.
VI. Итог урока. – Что нового узнали на уроке? – Какие числа называют однозначными? – Какие называют двузначными? Домашнее задание: № 13, 14 (учебник); № 9, 10 (рабочая тетрадь). Урок 5 Двузначные числа и их запись Цели урока: продолжить формирование навыка чтения и записи двузначных чисел; познакомить учащихся с правилами работы на калькуляторе; составить алгоритм набора двузначного числа на калькуляторе; учить выделять симметричные фигуры и строить оси симметрии; совершенствовать вычислительные навыки; развивать умение анализировать и обобщать. Ход урока I. Организационный момент. II. Устный счет. 1. Рассмотрите чертеж и выпишите названия всех треугольников. 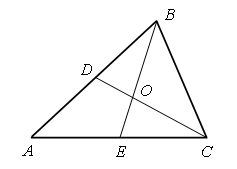 2. Отгадайте, какое слово зашифровано.
3. Решите задачу. Кролик разбил свой огород на грядки: 4 грядки для моркови, 7 грядок для капусты и 2 грядки для репы. Сколько грядок на огороде Кролика? 4. Чему равна масса арбуза? Чему равна масса дыни?  III. Сообщение темы урока. – Из чисел 2, 4, и 5 составьте и запишите все возможные двузначные числа. Запись: 22, 24, 25, 44, 42, 45, 55, 52, 54. – Прочитайте полученные числа. – Сегодня на уроке продолжим учиться читать и записывать двузначные числа. IV. Работа над новым материалом. Задание № 4 (с. 12). – Вспомните правила чтения двузначных чисел. – Прочитайте числа в задании. |
