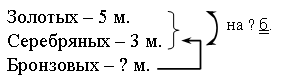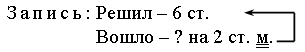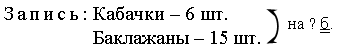|
|
урок математики. Учебник для учащихся общеобразовательных учреждений в 2 ч. В. Н. Рудницкая, Т. В. Юдачева. М. ВентанаГраф, 2010
Задание № 5 (с. 12).
Учащиеся вводят на калькуляторе данные числа.
– Как включить калькулятор?
– Как правильно набрать на калькуляторе двузначное число?
– Какая кнопка выполняет команду «сброс»?
Задание № 6 (с. 12).
Учащиеся выполняют алгоритм сложения на калькуляторе.
V. Повторение пройденного материала.
1. Работа с учебником.
Задание № 17 (с. 14).
Измерения учащиеся выполняют непосредственно на рисунках в учебнике.
Высота катушки – 3 см.
Длина магнитофонной кассеты – 7 см, ширина – 4 см.
Задание № 18 (с. 14).
– Какие фигуры являются симметричными?
– Рассмотрите таблицу на доске и назовите симметричные фигуры. (Только фигуры 3, 5.)
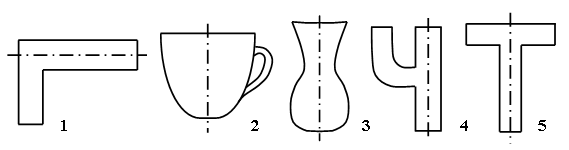
– Рассмотрите рисунок в учебнике и найдите в нем симметричные фигуры.
Далее учащиеся работают с квадратами, вырезанными из цветной бумаги (квадраты заранее готовятся дома).
– Определите, есть ли оси симметрии у квадрата.
– Если квадрат «перегнуть» по данной прямой, то части, на которые эта прямая разбивает квадрат, совпадут. Эта прямая – ось симметрии квадрата.
– Проведите еще ось симметрии квадрата.
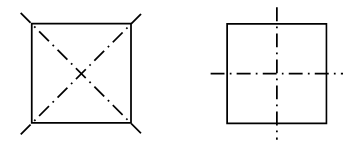
– Сколько осей симметрии у квадрата? Начертите квадрат в тетради и покажите все оси симметрии.
– Проверьте свой ответ на вырезанных квадратах, согнув по этим прямым.

– Какие фигуры в учебнике имеют оси симметрии?
– На рисунке изображены три предмета. У платка треугольной формы одна ось симметрии. У салфетки, имеющей форму квадрата, четыре оси симметрии. Угольник не имеет оси симметрии.
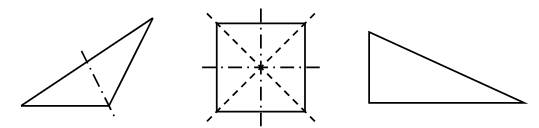
– Почему платок треугольной формы имеет ось симметрии, а угольник (тоже треугольной формы) не имеет оси симметрии? (Платок имеет форму равнобедренного треугольника.)
Задание № 19 (с. 14).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи и решите ее.
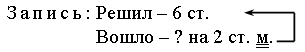
Решение:
6 – 2 = 4 (ст.)
Ответ: 4 столбика.
Задание № 21 (с. 15).
– Прочитайте условие задачи.
– Что известно? Что требуется узнать?
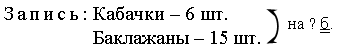
Решение:
15 – 6 = 9 (шт.)
Ответ: на 9 баклажанов купили меньше.
2. Работа в печатной тетради № 1.
Задание № 11.
При выполнении второй части задания учащиеся должны воспользоваться одним из двух правил сравнения натуральных чисел, изученных еще в 1 классе: «Из двух чисел меньше то, которое называют при счете раньше, и больше то, которое называют при счете позже». Это правило автоматически переносится на новую область натуральных чисел (от 20 до 100). Сложность заключается в том, что ряд чисел, из которого надо выбрать большее и меньшее числа, записан в обратном порядке, поэтому первое число в ряду (84) будет наибольшим, а последнее (79) – наименьшим.
Задание № 12.
Учащиеся работают самостоятельно. Далее учитель проводит проверку.
– Докажите, что вы верно провели стрелки.
С этой целью ученики устно называют по порядку все натуральные числа в выбранном промежутке. Если среди этих чисел будет названо число и на номерке, то соответствующая стрелка проведена правильно.
Задание № 13.
Для решения этой задачи в качестве модели (вместо фишек) можно использовать цветные палочки.
По условию задачи папа нашел 3 десятка грибов, а Алеша – 8 грибов. Выложим с помощью цветных палочек эти числа.
Так как в задаче спрашивается, сколько всего грибов принесли домой папа и Алеша, значит, надо сложить (сдвинуть на модели) эти числа:
Получилось число, в котором 3 десятка (3 оранжевые палочки) и 8 единиц (8 белых палочек), – 38. Значит, папа и Алеша принесли домой 38 грибов. В тетради решение задачи записывается так:
Решение:
30 + 8 = 38 (гр.).
Ответ: 38 грибов.
VI. Итог урока.
– Что нового вы узнали на уроке?
– Какие фигуры называют симметричными?
– Что такое ось симметрии?
Домашнее задание: № 18 (учебник); № 14 (рабочая тетрадь).
Урок 6
Двузначные числа и их запись
Цели урока: познакомить учащихся с римскими цифрами; совершенствовать вычислительные навыки; продолжить формирование умений строить и читать математические графы; рассмотреть решение задачи разными способами; развивать умение сравнивать и рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Сколько всего отрезков на чертеже?
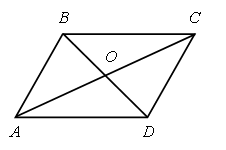
2. Помогите Незнайке найти ошибки.
8 + 6 = 14
|
12 – 4 = 7
|
6 + 7 = 12
|
7 + 9 = 16
|
16 – 8 = 8
|
8 + 5 = 12
|
4 + 8 = 13
|
13 – 6 = 7
|
9 + 9 = 18
|
3. У кого масса меньше – у собаки или у кошки?
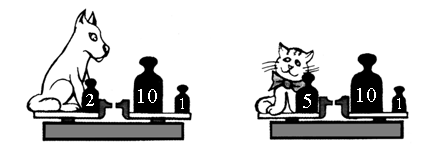
4. Решите задачу.
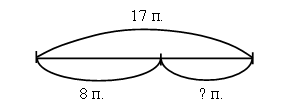
На свой день рождения Мальвина испекла пирожки и положила их на тарелку. После того как все гости взяли по одному пирожку, на тарелке осталось 8 пирожков. Сколько гостей пригласила Мальвина, если на тарелке было 17 пирожков?
III. Сообщение темы урока.
– Сегодня на уроке узнаем, как люди научились записывать числа.
IV. Работа над новым материалом.
– Какие числа называются однозначными? Двузначными?
– Назовите разряды двузначного числа.
Задание № 10 (с. 13).
– Какие двузначные числа можно записать цифрами 0, 2 и 4, если цифры в записи числа не повторяются?
Запись: 20, 40, 24, 42.
– Что такое цифра? Что такое число?
– Сколько цифр вы знаете?
– Сколько чисел в математике? Можете ли вы назвать наибольшее число?
Задание № 11 (с. 13).
– С помощью каких цифр можно записать все возможные двузначные числа?
Запись: 55, 51, 11, 15.
Задание № 16 (с. 14).
Запись: 10, 20, 30, 40, 50, 60, 70, 80, 90.
15, 25, 35, 45, 55, 65, 75, 85, 95.
– Почему количество чисел в этих числовых рядах совпадает?
V. Путешествие в прошлое. Знакомство с римскими цифрами.
Как люди научились записывать числа
– Сегодня мы отправимся в путешествие в Древний Египет, Индию, Вавилон и узнаем, как записывали цифры и числа разные народы. Очень разные и даже забавные были эти «цифры».
В Древнем Египте, например, числа первого десятка записывались соответствующим количеством палочек: – 1, – 2 и т. д. Десять обозначали в виде подковы – Чтобы записать число 15, нужно было поставить одну подкову и пять палочек:
В Индии за две тысячи лет до начала нашего летосчисления появился ноль. Его обозначили так же, как и сейчас. Но ведь мы уже привыкли к нему, а тогда это было великим открытием. Назывался он в то время просто кружком. А в Древней Индии кружок – сунья. Арабы перевели это слово как цифр. Не правда ли, напоминает что-то?
Правильно! Цифр – цифра. Так уж получилось, что арабским именем нуля стали называть все остальные знаки. Все они теперь цифры: и 0 – цифра, и 5 – цифра, и 9 – цифра. А само слово ноль возникло позже от латинского nullum – ничто.
После того как был создан алфавит, во многих странах числа стали записывать с помощью букв. В Древней Греции и Древней Руси к буквам добавляли еще специальные знаки, чтобы не путать их с обычными буквами.
Немало различных способов записи чисел было создано людьми. В Древней Руси числа обозначали буквами с особымзнаком«
» (титло), который писали над буквой.
Первые девять букв алфавита обозначали единицы, следующие девять букв – десятки, а последние девять букв – сотни. Число десять тысяч называли словом «тьма» (и теперь мы говорим: «народу – тьма тьмущая»).
Современная достаточно простая и удобная десятичная система записи чисел была заимствована европейцами у арабов, которые, в свою очередь, переняли ее у индусов. Поэтому цифры, которыми мы сейчас пользуемся, европейцы называют «арабскими», а арабы – «индийскими». Эта система была введена в Европе примерно в 1120 году английским ученым-путешественником Аделардом. К 1600 году она была принята в большинстве стран мира.
Русские названия чисел тесно связаны с десятичной системой счисления. Например, семнадцать означает «семь на десять», семьдесят – «семь десятков», а семьсот – «семь сотен».
Однако и эта система оказалась очень громоздкой.
Всем с детства знакома римская нумерация. Чаще всего римские цифры встречаются на циферблате в часах:
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
IX
|
X
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
До сих пор используются римские цифры, которые употреблялись в Древнем Риме уже около 2500 лет тому назад.
I – 1, V – 5, X –10, L – 50, G – 100, D – 500, M – 1000
Остальные числа записываются этими же цифрами с применением сложения и вычитания. Так, например, число XXVII означает 27, так как 10 + 10 + 5 + 1 + 1 = 27.
Если меньшая по значению цифра (I, X, С) стоит перед большей, то ее значение вычитается.
Например: IV означает 4 (5 – 1 = 4), IX означает 9 (10 – 1 = 9). ХС означает 90. Таким образом, число MCMLXXXIX означает 1989, так как:
1000 + (1000 – 100) + 50 + 10 + 10 + 10 + (10 – 1) = 1989.
В настоящее время римские цифры обычно применяются при нумерации глав и разделов книги, месяцев года, для обозначений дат значительных событий, годовщин.
Для вычислений запись чисел с помощью римских цифр неудобна. В этом вы можете убедиться сами, если попробуете выполнить, например, сложение чисел CCXCVII и XLIX или деление числа CCXCVII на число IX.
Большим достижением стало введение нуля, который позволил при записи чисел указывать пропущенный разряд. Способ записи любого числа с использованием всего только десяти цифр 1 2 3 4 5 6 7 8 9 0 был изобретен в Индии. Эта система оказалась настолько простой и удобной, что быстро распространилась по всем странам, а так как распространяли ее именно арабы, а не индусы, то эти цифры мы стали называть арабскими.
VI. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 22 (с. 15).
– Прочитайте текст. Можно ли его назвать задачей? Почему? (Нет вопросов.)
– Придумайте несколько вопросов, чтобы получились разные задачи.
Варианты вопросов:
Сколько получили бронзовых медалей?
Сколько всего получили медалей?
На сколько золотых медалей получили больше, чем серебряных? И т. д.
Далее необходимо разобрать и решить полученные задачи.
Запись:

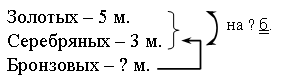
Задание № 24 (с. 16).
– Прочитайте задание.
– Рассмотрите иллюстрацию. Что вы видите на рисунке?
– Сколько тарелок?
– Сравните число яблок на одной тарелке с числом яблок на другой. Сколько их на каждой тарелке?
– Составьте по рисунку задачу на сложение. (Сколько всего яблок на четырех тарелках, если на каждой лежит по 6 яблок?)
– Составьте по рисунку задачу на вычитание. (Было 24 яблока, съели 6 яблок. Сколько яблок осталось?)
Далее переходим к составлению задачи на умножение, например: мама разложила на 4 тарелках по 6 яблок. Сколько всего яблок разложила мама по тарелкам?
Задача решается с помощью фишек. Ее решение записывается в тетрадь:

Теперь можно переходить к составлению задачи на деление. Здесь могут быть два варианта:
1. Раскладываем 24 яблока на 4 тарелки поровну. Надо найти, сколько яблок оказалось на каждой тарелке.
2. Раскладываем 24 яблока на тарелки по 6 штук на каждую. Надо найти, сколько тарелок потребуется.
И в том и в другом случае задача решается действием деления. Желательно рассмотреть с детьми оба варианта: сначала решить практически эти задачи на фишках, а затем записать решение в тетрадь.
1. Решение:
24 : 4 = 6 (ябл.).
Ответ: 6 яблок.
|
2. Решение:
24 : 6 = 4 (т.).
Ответ: 4 тарелки.
| |
|
|
 Скачать 2.65 Mb.
Скачать 2.65 Mb.