урок математики. Учебник для учащихся общеобразовательных учреждений в 2 ч. В. Н. Рудницкая, Т. В. Юдачева. М. ВентанаГраф, 2010
 Скачать 2.65 Mb. Скачать 2.65 Mb.
|
|
Задание № 6 (с. 18). Чертежи:  – Волк и Заяц тоже выполнили это задание. Рассмотрите их чертежи. Кто из них прав? Объясните свой ответ. – Какие ошибки у них допущены? 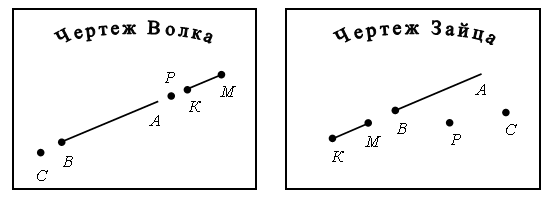 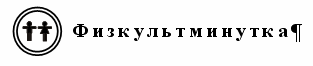 V. Повторение пройденного материала. 1. Работа в печатной тетради № 1. Задание № 23. Направления движения Маши и Миши задаются лучами. Общее начало этих двух лучей изображено на рисунке точкой. Так как Маша и Миша пошли в противоположных направлениях, то дляпостроения сразу обоих лучей удобно линейку расположить так:  Задание № 25. Скорее всего, дети предложат следующие решения: 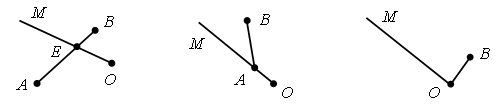
Можно дать дополнительное задание, направленное на выявление глубины усвоения материала: «Волк и Заяц тоже выполнили это задание. Рассмотрите чертежи. Справились ли с заданием Волк и Заяц? Свой ответ поясните». 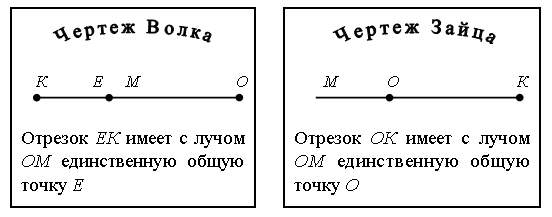 (Чертежи заранее делаются учителем.) Если у учащихся правильно сформировано представление о луче, то они увидят, что с заданием справился только Заяц. 2. Работа по учебнику. Задание № 13 (с. 20). – Вспомните правила построения графа. Решение: 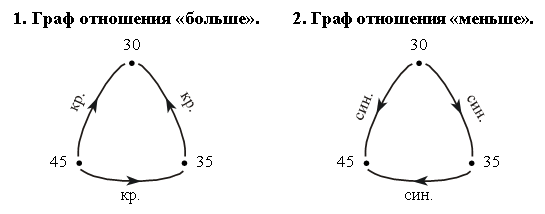 Задание № 16 (с. 21). – Прочитайте задачу. – Что известно? Что требуется узнать? – Как вы думаете, можно ли изменить условие задачи так, чтобы число 6 называлось только один раз? Новая формулировка задачи: У Бори 6 простых и столько же цветных карандашей. Сколько карандашей у Бори? – Запишите решение новой задачи. Задание № 19 (с. 21). – Прочитайте условие задачи. – Что известно? Что требуется узнать? – Используя цветные палочки, решите эту задачу. Рассуждение: «По условию задачи Братец Кролик посадил 2 десятка семян моркови и 3 десятка семян редиса. Выложим с помощью цветных палочек эти числа:
Так как в задаче спрашивается, сколько морковок и редисок надеется собрать Братец Кролик, надо сложить (сдвинуть на модели) эти числа:
Получилось число, в котором 5 десятков (5 оранжевых палочек), – это 50. Значит, Братец Кролик надеется собрать 50 морковок и редисок». В тетради запишем решение задачи: 20 + 30 = 50 (к.). Ответ: 50 корнеплодов. – Прочитайте еще раз вопрос задачи. – Как вы думаете, почему в вопросе задачи используется слово «надеется»? – Можем ли мы точно утверждать, что Братец Кролик осенью соберет ровно 50 морковок и редисок? Почему? – Скорее всего, он соберет меньше 50 морковок и редисок или ровно 50? – Можем ли мы точно утверждать, что Братец Кролик не соберет больше 50 морковок и редисок. Почему? Справочный материал для учителя Понятие числового луча вводится после того, как дети освоят чтение и запись двузначных чисел. С помощью числового луча учащиеся осваивают еще один способ сравнения двузначных чисел: чем левее точка расположена на числовом луче, тем ее координата меньше; чем правее, тем ее координата больше. Числовой луч в математике часто называют координатным лучом. Эти термины являются синонимами. Во 2 классе в активный словарь учащихся вводятся термины: числовой луч, начало луча, единичный отрезок, координата точки (без определений), а также используются обозначения числового луча и координаты точки. Дети должны понять, что единичный отрезок – это отрезок, длина которого равна условно выбранной единице, начало луча обозначается точкой О, а сам числовой луч – буквами ОХ (читается: луч О – икс); координата точки записывается числом, заключенным в скобки; например, запись А(3) читается так: «Точка А с координатой три, или координата точки А равна трем. Координата точки О считается равной нулю, координата любой точки, отмеченной на луче, – это ее расстояние в единичных отрезках от начала луча (точки О)». Луч обозначают двумя буквами латинского алфавита, записывая их в строго определенном порядке: первой пишут букву, обозначающую начало луча. Так как у луча нет конца, то вторая буква не обозначает никакой точки луча и ее пишут над или под лучом в любом месте. Например, на рисунке изображен луч СМ, точка С – начало луча.  Точка X лежит на луче АВ, а точка Y на нем не лежит. В этом легко убедиться, приложив линейку к лучу АВ. 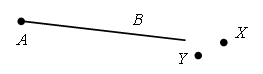 Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией, состоящей из конечного числа отрезков, вместе с этой ломаной. Отрезки ломаной называют сторонами многоугольника. На рисунке изображен многоугольник МАВКСЕ. Читать обозначение многоугольника можно, начиная с любой его вершины и в любом направлении. 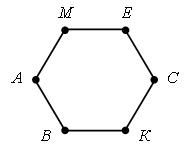 VI. Итог урока. – Что нового узнали на уроке? – Назовите признаки луча. Домашнее задание: № 17, 18 (учебник); № 24 (рабочая тетрадь). Урок 9 Луч и его обозначение Цели урока: продолжить формирование навыка изображения луча с помощью линейки и обозначения луча буквами; сравнить геометрические фигуры луч и отрезок; совершенствовать навыки решения задач разными способами; рассмотреть объемные тела: куб, цилиндр, конус; развивать умение сравнивать и рассуждать. Ход урока I. Организационный момент. II. Устный счет. 1. Сколько всего отрезков на чертеже? 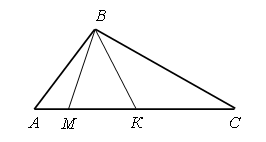 2. Разгадайте закономерность и заполните пустые «окошки». 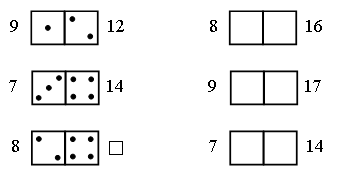 3. Решите задачу. Фокусник достал из волшебной шляпы 3 голубей, 7 сорок и 2 попугайчиков. Сколько птиц вытащил фокусник из волшебной шляпы? 4. Нарисуйте девятую фигуру, используя существующую закономерность. 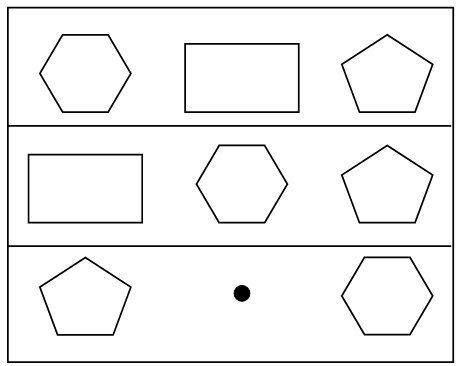 III. Сообщение темы урока. – Рассмотрите чертежи на доске: 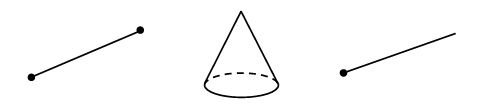 – Какое изображение будет «лишним»? Почему? – Как называется первая фигура? (Отрезок.) – Как называется последняя фигура? (Луч.) – Сегодня на уроке проведем сравнение этих фигур. IV. Работа над новым материалом. Задание № 7 (с. 19). – Рассмотрите чертежи. – Что объединяет все фигуры? (Это геометрические фигуры.) – Найдите на рисунке лучи и назовите их. (CD, OE.) – Что такое луч? – Как правильно прочитать луч? – Как называются остальные фигуры на рисунке? (Отрезки.) – Что такое отрезок? – Чем отличается луч от отрезка?
Задание № 8 (с. 19). Чертежи: а) отрезок лежит на луче: 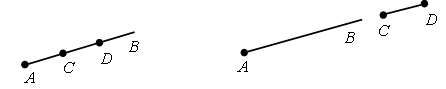 б) отрезок пересекает луч:  в) отрезок не пересекает луч: 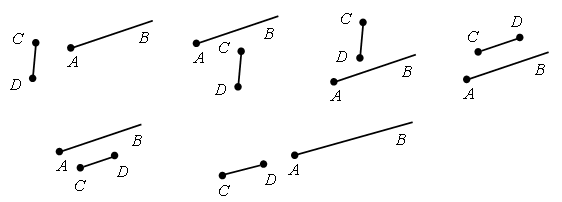 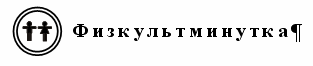 V. Повторение пройденного материала. 1. Работа по учебнику. Задание № 20 (с. 22). – Прочитайте условие задачи. – Что известно в задаче? Что надо узнать? – Запишите кратко условие задачи и решите ее. Запись: Было – 15 д. Ушли – ? д., 5 д. и 3 д. Осталось – ? д. Решение:
Задание № 22 (с. 22). – Сколько в коробке было цветных карандашей? – Сколько простых? – Сколько взяли из коробки карандашей? – Какие же могли быть эти карандаши? Учащиеся заполняют таблицу:
Задание № 23 (с. 22). Решение: 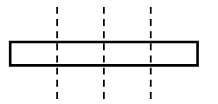 Чтобы распилить на 4 части, надо сделать 3 распила. 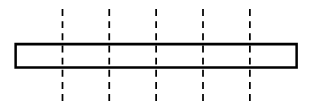 Чтобы распилить на 6 частей, надо сделать 5 распилов. 2. Работа в печатной тетради № 1. Задание № 27. – Прочитайте текст. – Является ли этот текст задачей? Почему? – Какие вопросы можно поставить к этому условию? Варианты вопросов: Сколько цветных снимков сделал фотограф? Сколько всего снимков сделал фотограф? Далее устно разбирается план решения обеих задач. В тетрадь учащиеся записывают решение своей задачи. Задание № 28. – Из каких чисел состоит данный ряд? (Только из «круглых» чисел.) – Вставьте пропущенные числа. (30, 60, 70, 90.) Наименьшим в этом ряду является число 10 (его первым называют при счете, следовательно, именно это число надо обвести синим карандашом), а наибольшим – 100 (его последним называют при счете, следовательно, именно это число надо обвести красным карандашом). Задание № 29. – Прочитайте задачу. – Какие цветы у Вали? (Гвоздики.) – Сколько у нее гвоздик? (7 гвоздик.) – Какие цветы у ее брата? (Розы.) – Что сказано о розах в условии задачи? («Столько же роз».) – Сколько же роз у брата? Далее учащиеся заполняют таблицу:
Решают задачу учащиеся самостоятельно. 3. Работа по карточкам. – Рассмотрите чертежи. Что объединяет эти фигуры? (Это объемные фигуры, геометрические тела.) – Как они называются? (Цилиндр, конус, куб.) – Какими линиями на чертеже показывают невидимые элементы геометрических тел? (Штриховой линией.) Для того чтобы учащимся легче было справиться с заданием, учитель может поставить перед ними модели цилиндра, конуса и куба. Непосредственно сравнивая модель каждой фигуры с ее изображением, учащиеся выделяют видимые и невидимые элементы каждого объемного тела и отражают свои наблюдения на чертеже. 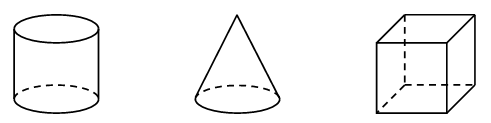 VI. Итог урока. – Что нового узнали на уроке? – Чем отличается луч от отрезка? – Назовите геометрические тела. – Как на чертеже геометрических тел показать невидимые линии? Домашнее задание: № 21 (учебник); № 26 (рабочая тетрадь). Справочный материал для учителя Пирамида Пирамидой называется многогранник, образованный всеми отрезками, соединяющими данную точку – вершину пирамиды – с точками плоского многоугольника – основания пирамиды. Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей ей стороной – сторона основания пирамиды. Боковыми ребрами пирамиды называются ребра, соединяющие вершину пирамиды с вершинами основания. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. На рисунке 1 изображена пирамида. Ее основанием является многоугольник А1А2... Аn, вершина пирамиды – S, боковые ребра – SA1, SA2, … , SAn, высота пирамиды – SX. Пирамида называется п-угольной, если в ее основании лежит п-угольник. Треугольная пирамида называется также тетраэдром. 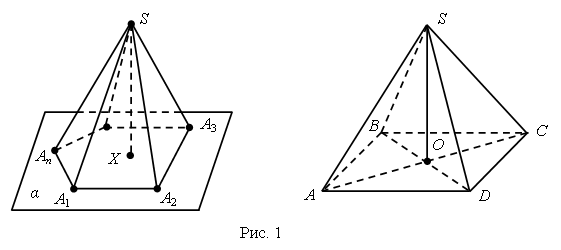 Цилиндр Цилиндром (точнее круговым цилиндром) называется тело, образованное заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, пересекающих круг в одной из плоскостей. Отрезки с одним концом на окружности этого круга называются образующими цилиндра. Поверхность цилиндра состоит из оснований цилиндра – двух равных кругов, лежащих в параллельных плоскостях, и боковой поверхности. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. В дальнейшем мы будем рассматривать только прямой цилиндр, называя его для краткости просто цилиндром. На рисунке 2 изображен прямой цилиндр. Он образован отрезками XX'параллельных прямых, заключенными между параллельными плоскостями α и α'. Его основаниями являются круги К и К' в этих плоскостях. 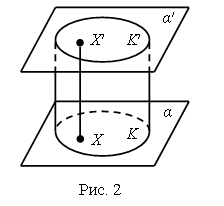 Прямой цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси (рис. 3). 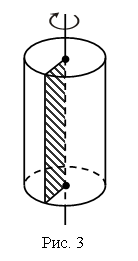 Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
