урок математики. Учебник для учащихся общеобразовательных учреждений в 2 ч. В. Н. Рудницкая, Т. В. Юдачева. М. ВентанаГраф, 2010
 Скачать 2.65 Mb. Скачать 2.65 Mb.
|
|
Конус Конусом (точнее круговым конусом) называется тело, образованное всеми отрезками, соединяющими данную точку – вершину конуса – с точками некоторого круга – основания конуса. 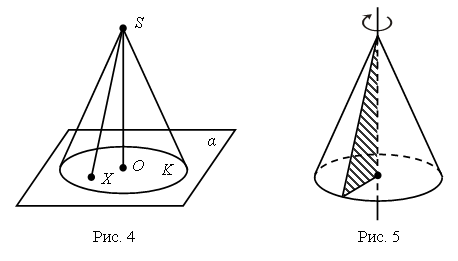 Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности. Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом. На рисунке 4 изображен прямой конус. Его вершиной является точка S, а основанием – круг К в плоскости α. Конус образован всеми отрезками SX, соединяющими вершину S с точками X основания. Прямой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси (рис. 5). Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого конуса называется прямая, содержащая его высоту. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса. Урок 10 Числовой луч Цели урока: познакомить учащихся с понятием «числовой луч»; ввести понятие о единичном отрезке на числовом луче; совершенствовать навыки составления и решения задач; продолжить работу с математическими графами; развивать логическое мышление и умение рассуждать. Ход урока I. Организационный момент. II. Устный счет. 1. Найдите примеры с ответом 12. Запись:
2. В каждой строке вместо точек вставьте недостающие фигуры, сохранив порядок их чередования. 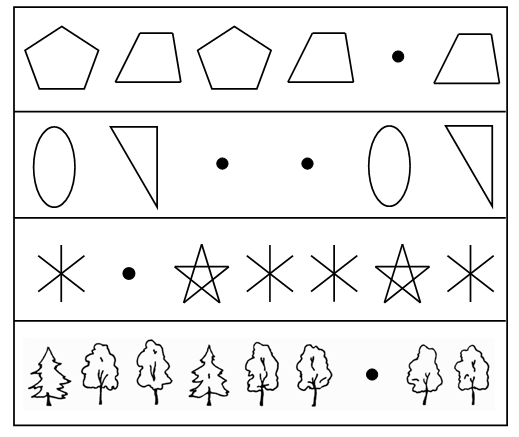 3. Из 9 счетных палочек составьте 5 треугольников. Сверьте с образцом. 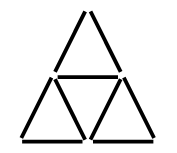 III. Сообщение темы урока. – Рассмотрите рисунок на доске.  – Как называются эти геометрические фигуры? – Название какой фигуры вы не знаете? – Сегодня на уроке мы научимся строить эту фигуру и узнаем, как ее называют. IV. Работа над новым материалом. На прошлых уроках вы познакомились с лучом, научились его изображать, обозначать буквами, читать обозначения. Посмотрите, какой луч изображен на доске, прочитайте его обозначение.  Возьмем линейку со шкалой. Представим себе, что наша линейка, как и луч, бесконечна. Наложим шкалу линейки на луч ОХ так, чтобы начало шкалы 0 (нуль) совместилось с началом луча – точкой О, а шкала с числами расположилась по лучу ОХ:  Упростим рисунок: снимем изображение линейки и миллиметровые деления, оставив лишь числа 0, 1, 2, 3, ...  Получим луч, который называют числовым лучом. На числовом луче обычно рисуют стрелку (справа). Отрезок от 0 до 1 называют единичным отрезком. Единичный отрезок может быть любой длины. Числовой луч  Задание № 1 (с. 23). – Рассмотрите числовой луч, изображенный в учебнике. Что вы видите? – Где растет цветок? (В точке О.) – Точку О называют началом числового луча. – Какой жук сидит дальше от цветка? (Красный жук сидит в точке 1, а синий в точке 3, т. е. синий жук сидит на расстоянии трех единичных отрезков от начала луча. Значит, синий жук сидит дальше от цветка.) – Что находится в точке 5? (Большой камень.) Задание № 2 (с. 23). Учащиеся работают с линейкой. – Положите перед собой линейку. Рассмотрите ее шкалу. – Покажите штрих с числом, которое обозначает начало отсчета. (Точка 0.) – Какое самое большое число написано на шкале линейки? – Покажите отрезок шкалы от 0 до 1, от 1 до 2, от 2 до 3 и так далее до конца шкалы. Задание № 3 (с. 23). – Что изображено в учебнике? – Прочитайте название луча. (ОX.) – Какой буквой обозначено начало луча (начало отсчета)? – Измерьте длину отрезков между двумя любыми соседними штрихами. (1 см.) – Сравните длины этих отрезков. (Они равны.) – Прочитайте определение, данное в книге (с. 24).  V. Повторение пройденного материала. 1. Работа в печатной тетради № 1. Задание № 38. – Что изображено на рисунке? (Граф отношений «меньше» и граф отношений «больше».) – Какие правила помогут вам прочитать данные высказывания о числах? – Прочитайте все высказывания о числах на первом графе. Число 21 меньше числа 65. Число 65 меньше числа 70. – Каких стрелок не хватает? Изобразите их и прочитайте высказывания. 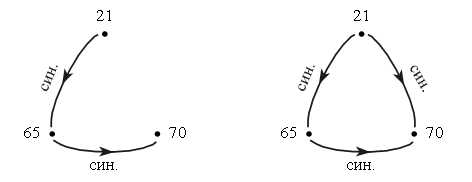 – Так как на графе точками отмечены три числа, то каждое из этих чисел должно соединяться синей стрелкой с каждым из двух других. Значит, появляется третье высказывание: число 21 меньше 70. – Рассмотрите второй граф. Каких стрелок не хватает? 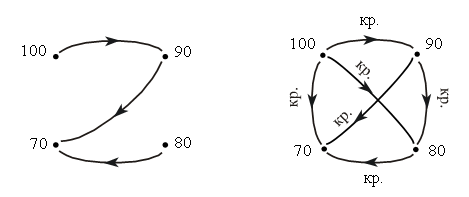 Читаем высказывания:
Задание № 40. – Рассмотрите данные иллюстрации. – Что вы узнали по ним? – Какие задачи можно составить к этим рисункам? Устно надо разобрать план решения всех составленных задач, но в тетрадь каждый ученик записывает решение той задачи, которую он составил сам. Варианты составленных задач: Мама и сын отдыхали в деревне у бабушки с 3 июня по 9 июня. Сколько дней они отдыхали в деревне? Миша и мама отдыхали на море с 10 июня по 15 июня. Сколько дней они были на море? Мама и сын сначала отдыхали в деревне, с 3 июня по 9 июня, а потом – на море, с 10 июня по 15 июня. Сколько всего дней они были и в деревне, и на море? – Где и на сколько дней больше отдыхали мама с сыном? 2. Работа с учебником. Задание № 10 (с. 26). Учащиеся записывают выражения с помощью арифметических действий и находят их значения. Задание № 11 (с. 26). – Что означают выражения «на 5 больше»? – «На 5 меньше»? Какие действия надо выполнить? – Устно ответьте на вопросы. Задание № 14 (с. 27). Задание позволяет проверить знание табличных случаев сложения и вычитания и уровень развития логического мышления детей. В первой части задания требуется назвать все возможные варианты решения. Необходимо сказать учащимся, что если они будут хаотично перечислять пары чисел, то могут пропустить какой-нибудь вариант. Нужно прежде всего придумать правило перебора решений, которое исключит вероятность пропуска той или иной пары. Например, будем перебирать по порядку (начиная с наименьшего) возможные варианты первого слагаемого и находить (исходя из условия) второе слагаемое. – Прочитайте задание. Что известно? – Сколько вариантов ответа имеет эта задача? – Как называются числа при сложении? Учащиеся заполняют таблицу:
Последние 5 решений повторяют первые пять решений, так как слагаемые в суммах одни и те же, но переставлены местами. Значит, в ответе указываем следующие возможные варианты пар: 0 и 9; 1 и 8; 2 и 7; 3 и 6; 4 и 5. – Прочитайте второе задание. – Можно ли перечислить все пары чисел, в результате вычитания которых получится 7? (Указать все такие пары невозможно.) – Как называются числа при вычитании? Далее учащиеся заполняют таблицу:
VI. Итог урока. – Что нового узнали на уроке? – Что такое числовой луч? – Как обозначают начало луча? – Что называют единичным отрезком? Домашнее задание: № 12, 13 (учебник); № 38, 40 (рабочая тетрадь). Урок 11 Числовой луч Цели урока: продолжить работу с числовым лучом; ввести понятие «координата точки на луче»; формировать умение строить числовой луч с заданным единичным отрезком; совершенствовать вычислительные навыки; рассмотреть решение задач разными способами; развивать логическое мышление и внимание. Ход урока I. Организационный момент. II. Устный счет. 1. Игра «Веселый счет».
2. Поставьте знак «+» или «–» так, чтобы равенства были верными.
3. Сравните тексты задач. Чем они похожи? Чем отличаются? Решите задачи.
III. Сообщение темы урока. – Прочитайте данные на доске записи:
– Какие у вас возникли затруднения? – Сегодня на уроке мы узнаем, что обозначает запись О(3). IV. Работа над новым материалом. Задание № 5 (с. 24). – Что изображено на рисунке? – Что называют числовым лучом? – Прочитайте его название. (ОВ.) – Какие числа соответствуют точкам М, К, А, В? (М – число 2, К – число 5, А – число 6, В – число 9.) – Как же называются эти числа?  – Итак, координата – это число. Давайте рассмотрим таблицу в учебнике на с. 25. Точка О, ее координата – нуль. Запись О(0) читают так: «Точка О с координатой нуль» или «Точка О имеет координату нуль». – Прочитайте таблицу до конца. – Прочитайте записи в таблице: М(2) и А(6). – Запишите в тетради координаты остальных точек. Запись: К(5), В(9). – А теперь научимся изображать числовой луч. Необходимо помнить о том, что числовой луч всегда чертят строго горизонтально в направлении слева направо. Направление надо указывать стрелкой. |
