урок математики. Учебник для учащихся общеобразовательных учреждений в 2 ч. В. Н. Рудницкая, Т. В. Юдачева. М. ВентанаГраф, 2010
 Скачать 2.65 Mb. Скачать 2.65 Mb.
|
|
III. Сообщение темы урока. – Рассмотрите чертежи на доске:  – Какую закономерность вы обнаружили? (У каждой следующей фигуры увеличивается количество углов и сторон на 1.) – Название каких фигур вы знаете? – Какие затруднения у вас возникли? – Как можно назвать все эти фигуры одним словом? – Об этом мы и будем говорить сегодня на уроке. IV. Изучение нового материала. – Вы уже умеете различать и изображать на бумаге такие фигуры, как треугольник, четырехугольник, пятиугольник. Такие фигуры обычно называют многоугольниками. Задание № 1 (с. 36). – Посмотрите на рисунок на с. 36 учебника. В верхней его части нарисовано печенье в форме многоугольников. Сколько углов имеет каждая из этих фигур? – Теперь рассмотрим желтый многоугольник, нарисованный в рамке. Сколько в нем углов? – Какой фигурой является каждая сторона многоугольника? (Отрезком.) – Сколько сторон у желтого многоугольника? – Какой фигурой является вершина многоугольника? (Точкой.) – Сколько вершин имеет желтый многоугольник? (Пять.) Вывод: в желтом многоугольнике 5 углов, 5 сторон и 5 вершин. Аналогично анализируется количество углов, сторон и вершин в зеленом и красном многоугольниках. – Что вы можете сказать о количестве углов, сторон и вершин в каждом многоугольнике? Вывод: в любом многоугольнике углов, сторон и вершин поровну. – Сколько же углов в семиугольнике? (7.) – Сколько вершин в десятиугольнике? (10.) – Сколько сторон в пятнадцатиугольнике? (15.) Далее учитель демонстрирует заранее подготовленный плакат с изображенным на нем четырнадцатиугольником. – Как определить название этого многоугольника? Что проще всего сосчитать? (Вершины.) Справочный материал для учителя Многоугольники Ломаная называется замкнутой, если у нее концы совпадают. Простая замкнутая ломаная называется многоугольником, если ее соседние звенья не лежат на одной прямой (рис. 1). Вершины ломаной называются вершинами многоугольника, а звенья ломаной – сторонами многоугольника. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями. Многоугольник с п вершинами, а значит и с п сторонами, называется п-угольником. 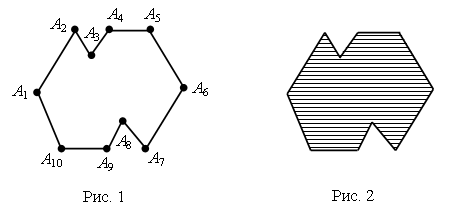 Плоским многоугольником или многоугольной областью называется конечная часть плоскости, ограниченная многоугольником (рис. 2). Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. При этом сама прямая считается принадлежащей полуплоскости. На рисунке 3 а изображен выпуклый многоугольник, а на рисунке 3 б – невыпуклый. Углом выпуклого многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине. 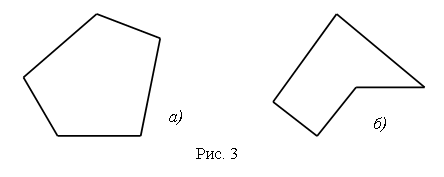 Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами. На рисунке 4 вы видите треугольник с вершинами А, В, С исторонами АВ, ВС, АС. Треугольник обозначается указанием его вершин. 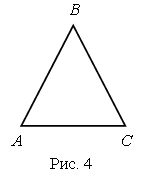 Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника, а соединяющие их отрезки – сторонами четырехугольника. На рисунке 5 представлены три фигуры, каждая из которых состоит из четырех точек А, В, С, D и четырех последовательно соединяющих их отрезков АВ, ВС, CD и AD. Четырехугольником является только третья фигура: у первой фигуры точки А, В, С лежат на одной прямой, а у второй – отрезки ВС и AD пересекаются. 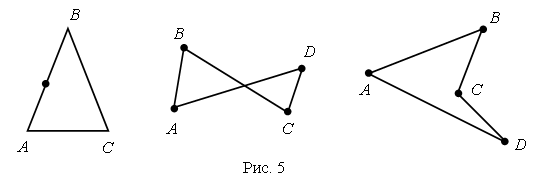 Вершины четырехугольника называются соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями. У четырехугольника на рисунке 6диагоналями являются отрезки АС и BD. 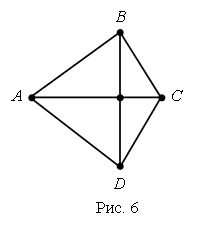 Стороны четырехугольника, исходящие из одной вершины, называются соседними сторонами. Стороны, не имеющие общего конца, называются противолежащими сторонами. У четырехугольника на рисунке 6 противолежащими являются стороны АВ и СD, BC и AD. Фронтальная работа. (Чертежи выполнены на доске заранее.) – Сосчитайте вершины многоугольника. Как он называется? (Четырнадцатиугольник.) 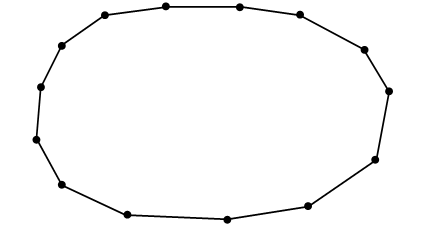 – А теперь попробуйте ответить на более сложные вопросы: бывают ли одноугольники? А двуугольники? Какой из многоугольников имеет наименьшее число углов? Как называется многоугольник, у которого 100 вершин? – Давайте научимся показывать элементы многоугольника: вершины, стороны и углы. Рассмотрим рисунок. (Сделайте его заранее на доске.) 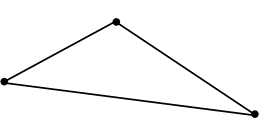 – Вершины – это точки. (Указкой покажите каждую вершину треугольника.) Теперь покажем стороны. Сторона многоугольника – это какая фигура? (Отрезок.) Показываем стороны как отрезки. (Конец указки движется от вершины, далее по отрезку до другой вершины.) Углы будем показывать вращением указки. Один конец указки должен находиться в вершине треугольника, сама указка – вдоль стороны, выходящей из этой вершины. Далее, не отрывая конца указки от вершины угла, двигаем указку по направлению к другой стороне, пока указка не совместится с этой стороной. Угол можно показать и дугой. (Продемонстрируйте учащимся, как правильно это сделать, и предложите им самостоятельно показать дугами каждый угол треугольника.) – Вершины треугольника обозначают буквами. Читать обозначение можно разными способами, начиная с любой вершины, например: треугольник АВС, АСВ, ВСА, ВАС, САВ, СВА. Задание № 2 (с. 37). – Что изображено на рисунке? (Многоугольники.) – Как называются данные многоугольники? (Треугольник, пятиугольник.) – Какими геометрическими фигурами являются вершины и стороны многоугольника? (Это точки и отрезки.) – Как принято обозначать точки на чертеже? (Прописной буквой латинского алфавита.) – А отрезки? (Двумя прописными буквами латинского алфавита.) – Назовите вершины треугольника. (О, М, К.) – Назовите стороны треугольника. (МО, МК, ОК.) – Сколько вершин и сколько сторон у этой фигуры? Аналогично учащиеся называют вершины и стороны пятиугольника. Задание № 3 (с. 37). Учащиеся вспоминают, что в любом многоугольнике число сторон, углов и вершин одинаково, причем многоугольник называется в соответствии с числом его сторон, углов и вершин. Так, в треугольнике по 3 стороны, вершины и угла, поэтому, для того чтобы сложить треугольник, потребуется 3 палочки. Аналогично учащиеся рассуждают при анализе четырехугольника и пятиугольника.  V. Повторение пройденного материала. 1. Работа в печатной тетради № 1. Задание № 50. Учащиеся раскрашивают третью слева фигуру в верхнем ряду и все фигуры – в нижнем. – Как называется каждый из раскрашенных многоугольников? – Какие еще известные вам фигуры изображены на чертеже? Задание № 51. – Какими геометрическими фигурами являются вершины и стороны многоугольника? (Это точки и отрезки.) – Каким карандашом мы должны раскрасить вершины? (Красным.) – Каким карандашом мы раскрасим стороны? (Синим.) – Как называются все многоугольники на чертеже? (Это четырехугольники.) – Сколько в четырехугольнике вершин? (Четыре.) – Сколько в нем сторон? (Четыре.) – Какой вывод вы можете сделать? (В каждом многоугольнике надо раскрасить красным цветом четыре точки – его вершины, а синим карандашом четыре отрезка – его стороны.) 2. Работа по учебнику. Задание № 8 (с. 38). – Что такое «сумма»? – Что называют «разностью»? Далее учащиеся называют суммы и разности чисел, указанных в задании. Задание № 9 (с. 38). – Что обозначает выражение «увеличить на…», «уменьшить на…»? Далее учащиеся записывают сложные выражения: (4 + 3) + 2 (15 – 9) – 5 (6 + 4) + 7 (11 – 5) – 4 (12 – 8) + 8. – Определите порядок выполнения действий и найдите значение каждого выражения. Задание № 10 (с. 38). – Прочитайте задачу. – Что вам известно? Что требуется узнать? – Запишите кратко условие и решите эту задачу. 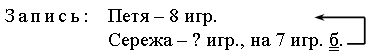 Решение: 8 + 7 = 15 (игр.) – у Сережи. Ответ: 15 игрушек. – Как изменить условие задачи, чтобы она решалась вычитанием? (На 7 игрушек меньше.) – Как изменить вопрос задачи, чтобы в ее решении было два действия? (Сколько игрушек всего?) Задание № 13 (с. 39). Учащиеся работают в парах, на калькуляторе набирают данные числа. VI. Итог урока. – Что нового узнали на уроке? – Какие фигуры называют многоугольником? – Как определить название многоугольника? – Как обозначают многоугольники на чертеже? Домашнее задание: № 7, 11 (учебник); № 53, 54, 56 (рабочая тетрадь). Урок 16 Многоугольник и его элементы Цели урока: учить определять количество углов в многоугольнике; обозначать латинскими буквами многоугольники; продолжить формирование навыков показывать вершины, стороны и углы в многоугольнике; совершенствовать навык решения задач; развивать умение сравнивать и обобщать. Ход урока I. Организационный момент. II. Устный счет. 1. Разгадайте правило, по которому составлена таблица, и заполните пустые клетки:
2. Вставьте пропущенные числа: 77, 78, 79, , 81, , 37, 47, 57, , , 87, 94, 84, 74, , , , 34 89, 87, 85, , , 79 3. Из 9 счетных палочек составьте 4 равных треугольника. Сверьте с образцами. 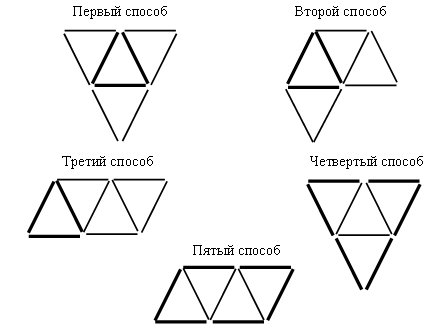 III. Сообщение темы урока. – Рассмотрите фигуры, изображенные на доске. 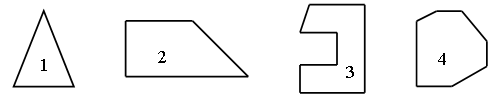 – Как называются эти фигуры? (Многоугольники.) – Назовите номер «лишнего» многоугольника. (3.) – Как называется этот многоугольник? Об этом мы узнаем сегодня на уроке. IV. Изучение нового материала. 1. Работа по учебнику. Задание № 4 (с. 37). – Рассмотрите рисунок. – Как определить название многоугольника? – Как называется первая фигура? (Четырехугольник.) – Как называется вторая фигура? (Шестиугольник.) – Покажите каждый угол многоугольника. – Покажите все стороны четырехугольника. – Покажите все вершины шестиугольника. Справочный материал для учителя Вершины многоугольника ученик показывает, касаясь каждой из них концом указки или карандаша; стороны – как отрезки, то есть ведя указкой по каждой стороне. Первое время лучше показывать каждый угол многоугольника вращением указки (карандаша) следующим образом: один конец указки помещается в вершине многоугольника, например в точке А, а сама указка располагается вдоль одной из сторон, выходящей из этой вершины. Не отрывая конца указки от вершины угла, двигаем указку в плоскости доски по направлению к другой стороне многоугольника до совмещения с ней. Такой способ показа угла облегчит в дальнейшем формирование представлений учащихся о видах углов (прямой, острый, тупой, развернутый), сравнении углов. В дальнейшем это учебное действие можно упростить: угол будем показывать дугой. 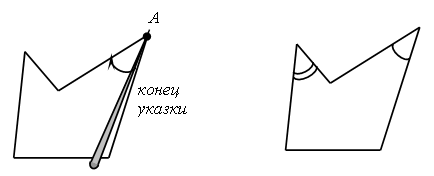 – Чем похожи многоугольники из задания № 4? – Эти многоугольники называются невыпуклыми. Многоугольники бывают выпуклые и невыпуклые. Многоугольник называется выпуклым, если он весь лежит по одну сторону от прямой, которой принадлежит какая-либо его сторона. Если это условие не выполняется, то многоугольник называется невыпуклым. 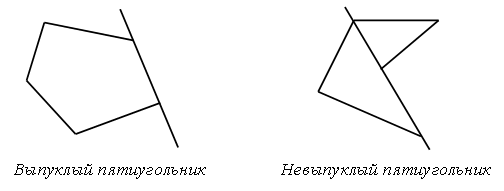 Задание № 5 (с. 37). – Рассмотрите рисунок. – Можно ли назвать этот многоугольник пятиугольником? Почему? (Чтобы выяснить, как называется этот многоугольник, можно пересчитать число его сторон. Их 7. Значит, это семиугольник. В нем не только 7 сторон, но и по 7 вершин и углов.) Задание № 6 (с. 37). Учащиеся строят в тетради треугольник и четырехугольник. 2. Работа в печатной тетради № 1. Задание № 52. Учащиеся должны зачеркнуть слова «треугольник» и «пятиугольник», так как фигуру на чертеже можно назвать и многоугольником, и четырехугольником, и квадратом.  V. Повторение пройденного материала. 1. Работа с учебником. Задание № 16 (с. 39). – Прочитайте задачу. – Что вам известно? Что требуется узнать? – Запишите кратко условие задачи. Запись: Было – 5 ог. и 4 п. Порезали – 3 ов. Осталось – ? ов. – Прочитайте, как Миша собирается решить задачу. (Выражением.) – Верна ли его запись? – Объясните, что обозначает выражение: – Запишите решение задачи по действиям. Решение: 1) 5 + 4 = 9 (ов.) – было. 2) 9 – 3 = 6 (ов.) – осталось. – Сравните свою запись с записью Миши. – Запишите решение задачи уравнением. 2. Фронтальная работа. – Рассмотрите каждый рисунок. Покажите отрезки АВ и CD. Есть ли у этих отрезков общая часть? Какой фигурой она является? 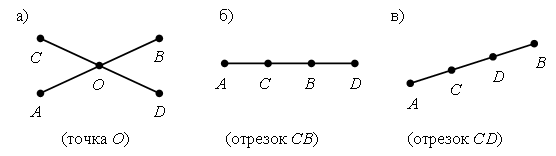 |
