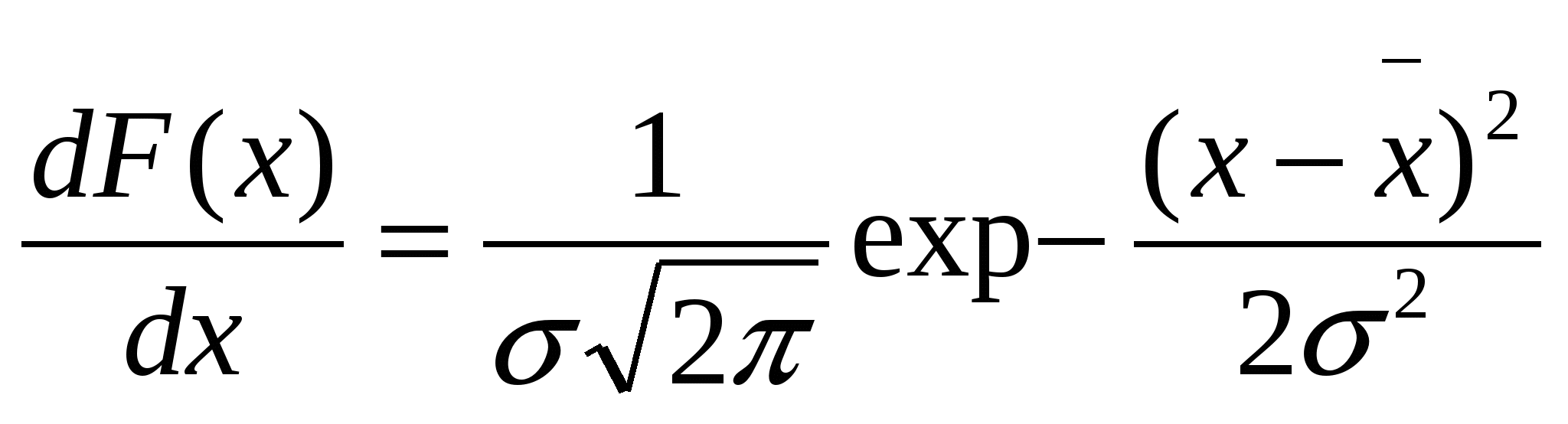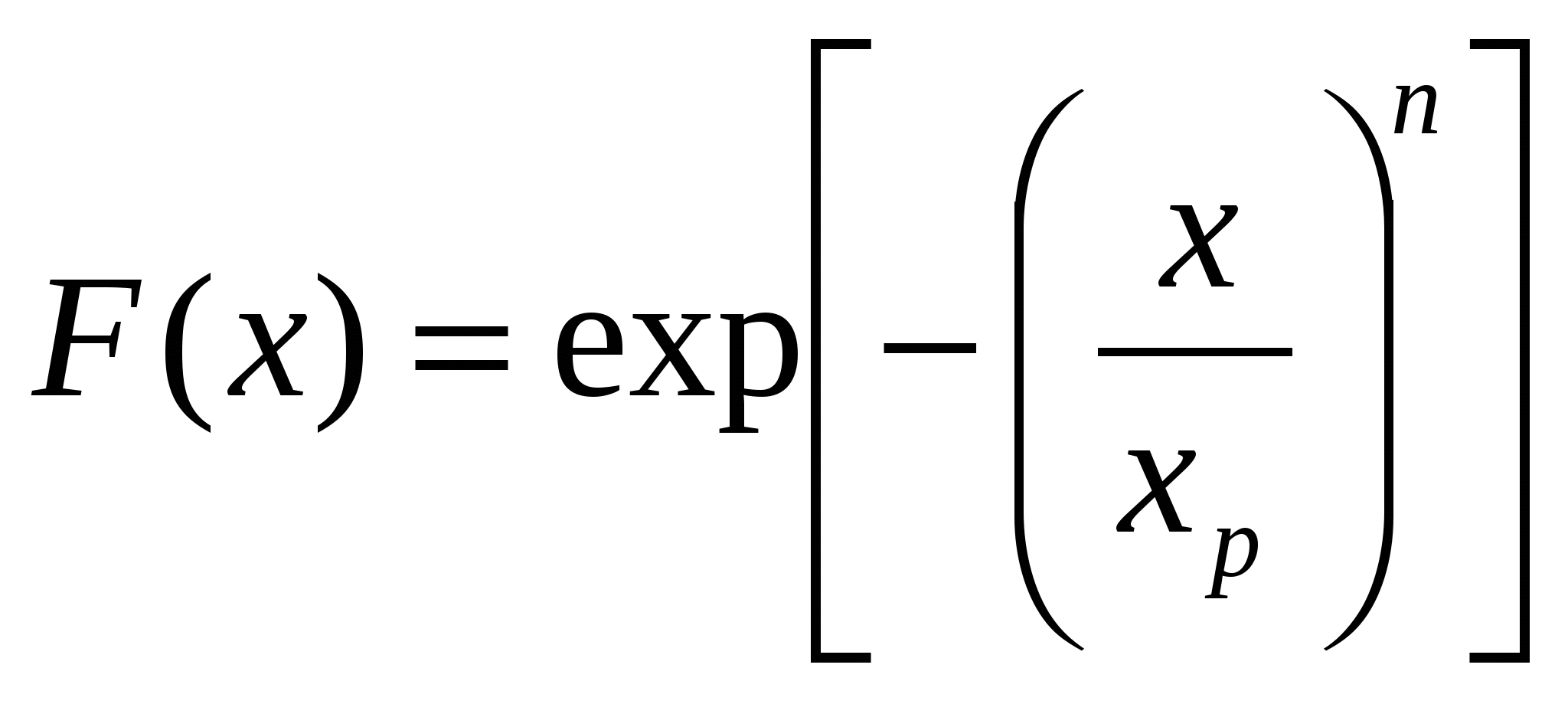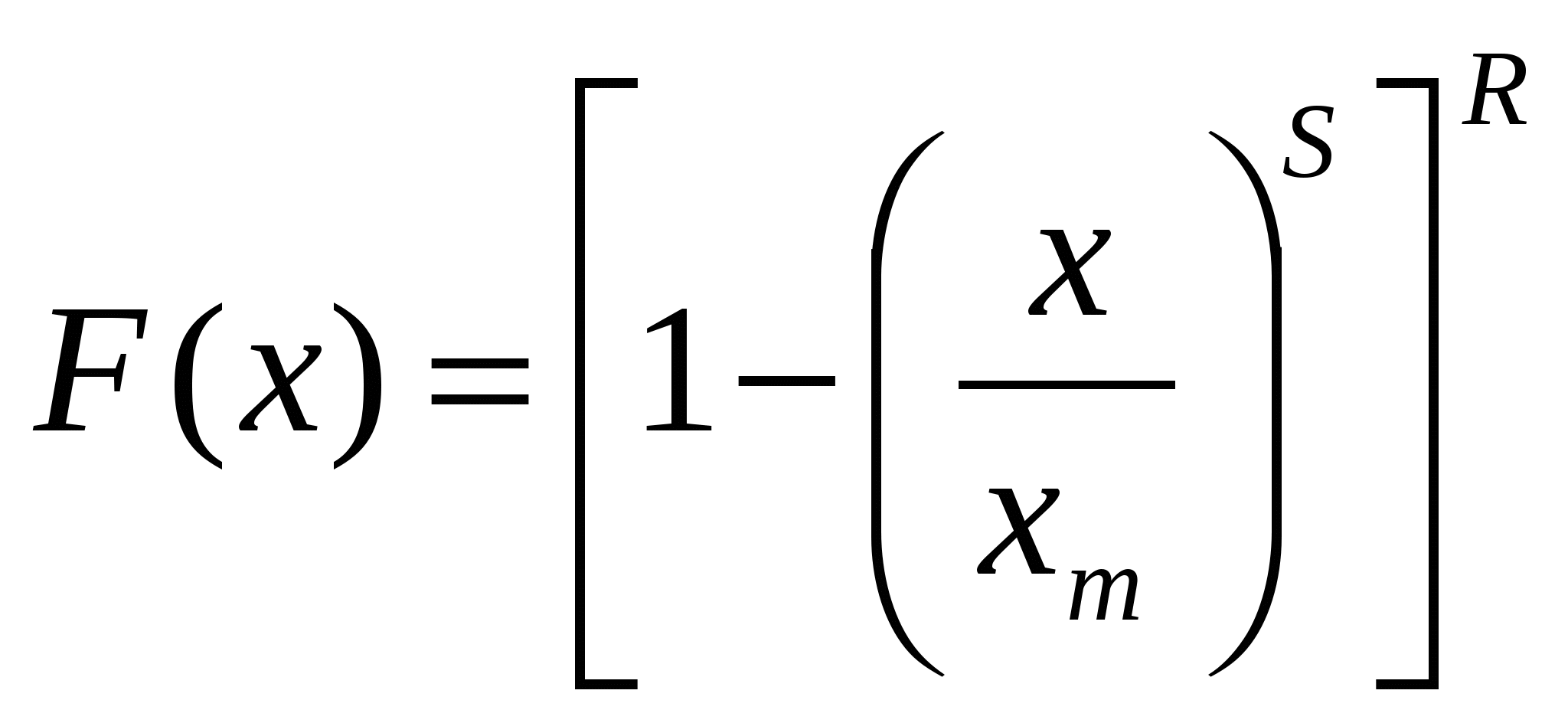ТОЗОС часть2. Учебнометодические разработки для самостоятельной работы студентов по курсу
 Скачать 7.02 Mb.
|
|
4.2.5. Характеристики крупности Характеристикой крупности называют графическое изображение гранулометрического состава сыпучего материала. Характеристики крупности строят в прямоугольной системе координат: частные - по выходам отдельных классов и суммарные (кумулятивные) - по суммарным выходам классов. При построении частной характеристики по оси абсцисс откладывают размер отверстий сит, применявшихся при ситовом анализе, а по оси ординат - выход соответствующих классов в процентах. Ординаты, определяющие выхода отдельных классов, строят на меньшем или большем из диаметров, ограничивающих данный класс, или на диаметре, равном среднему арифметическому значению двух крайних диаметров. Полученные точки соединяют. По выходам отдельных классов можно построить график, называемый в статистике столбиковой диаграммой. Последняя составляется из прямоугольников, высота которых пропорциональна выходам классов, а основанием служит интервал крупности классов. Пример построения частной характеристики крупности по выходам отдельных классов и столбиковая диаграмма (по данным табл. 4.12) показаны на рис. 4.14,а. Суммарную характеристику крупности Y = f(x) строят по точкам, положение которых находят по абсциссам х - диаметрам кусков и ординатам Y - суммарным выходам классов мельче или крупнее  ( х=l, где l - размер отверстий сита, через которые просеивается материал).Если по оси ординат отложены выхода материала, крупнее данного диаметра, то характеристика построена «по плюс х», если мельче данного диаметра, то - «по минус х». Обе характеристики зеркально отражают одна другую и, будучи построены на одном графике, пересекаются в точке, соответствующей выходу материала, равному 50%. Пример построения суммарных характеристик показан на рис. 4.14,б. Выход какого-либо класса  по суммарной характеристике определяется разностью ординат, построенных на диаметрах х1и х2.Суммарные характеристики «по плюс х» бывают выпуклыми, вогнутыми и прямолинейными. Выпуклая кривая получается при преобладании в материале крупных зерен, вогнутая - при преобладании мелких зерен. Прямолинейная кривая свидетельствует о равномерном распределении в материале зерен по крупности, т. е. на любом участке характеристики на единицу изменения диаметра приходится одинаковое изменение суммарного выхода материала. По виду частной характеристики заключения о распределении в материале крупных кусков и мелких зерен сделать нельзя, так как ее вид зависит от набора сит, применявшихся при ситовом анализе. Изменение шкалы сит изменяет и вид частной характеристики. По кривой суммарной характеристики можно определить выход любого класса крупности. При построении суммарных характеристик в широком диапазоне крупностей зерен материала отрезки на оси абсцисс в области мелких классов получаются весьма малого размера, что затрудняет построение и использование характеристик. Приходится строить непомерно большие графики. Чтобы избежать этого недостатка, суммарные характеристики строят в системе координат с полулогарифмическими или логарифмическими шкалами. 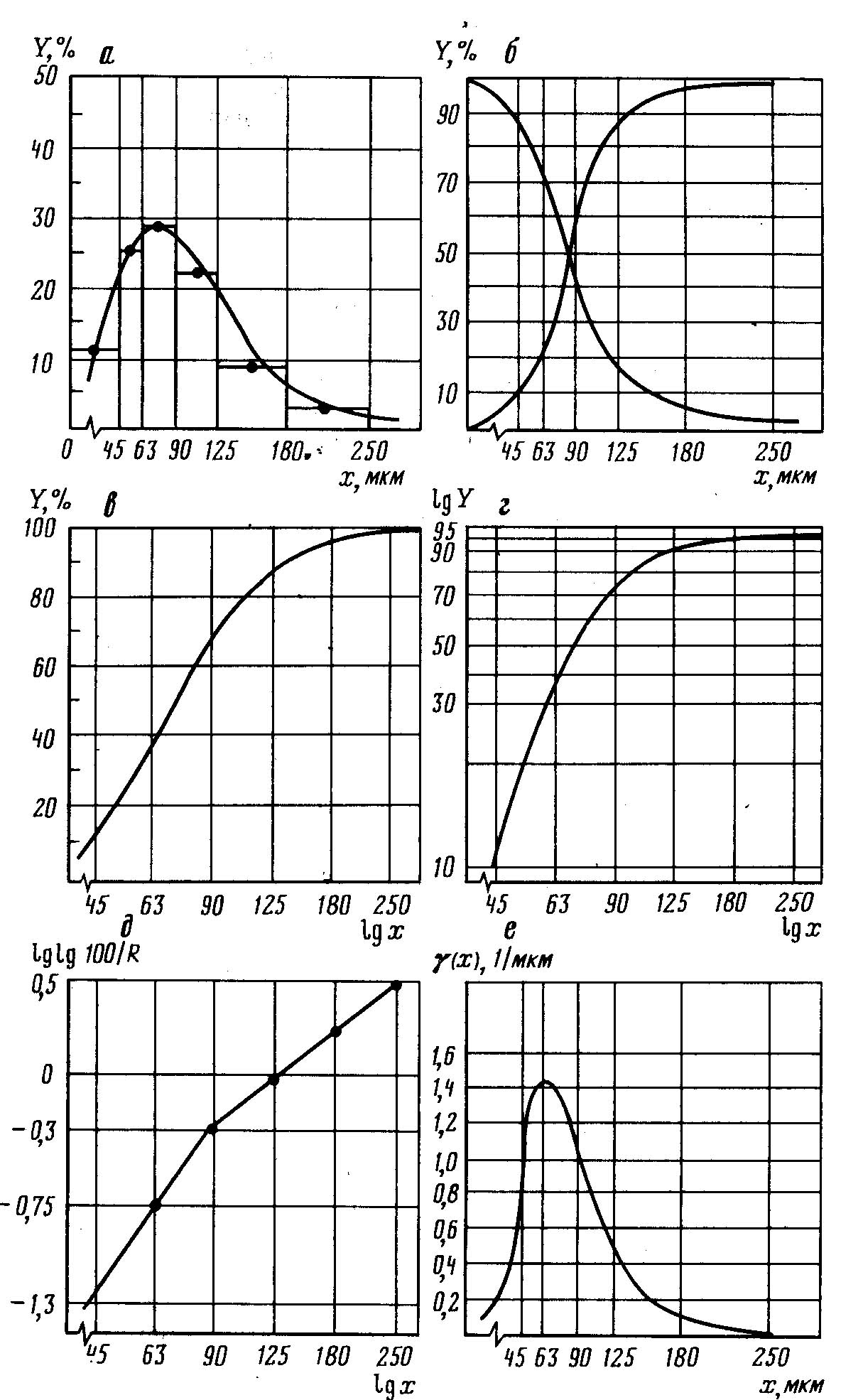 Рис.4.14. Графическое представление данных ситового анализа: а - частная характеристика крупности по выходам отдельных классов; б - суммарные характеристики крупности; в - полулогарифмическая характеристика крупности; г - логарифмическая характеристика крупности; д - характеристика крупности по Розину-Раммлеру; е - дифференциальная функция распределения по крупности Полулогарифмическую суммарную характеристику крупности строят в системе координат  где х=l - размер отверстий сита, Y - суммарный выход классов.Преимущество полулогарифмической кривой по сравнению с обыкновенной кривой Y= f(x) состоит в том, что расстояния между соседними значениями отверстий сит на оси абсцисс в области мелких зерен увеличиваются, а в области крупных - сокращаются, что позволяет более точно отсчитывать выхода мелких классов при обычном размере графика. Если набор сит, применяемых для ситового анализа, имеет постоянный модуль, то построение полулогарифмической характеристики значительно упрощается, так как отрезки на оси абсцисс будут одинаковой величины. Например, для ряда сит с постоянным модулем М разница между логарифмами размеров смежных сит (табл.4.13). Таблица 4.13 Характеристика сит с постоянным модулем.
Каждый отрезок на оси абсцисс между соседними ситами равен  . При построении характеристики за можно принять произвольный отрезок.Полулогарифмическая суммарная характеристика крупности (по данным табл. 4.12) показана на рис. 4.14, в. В отличие от обыкновенных кривых суммарной характеристики левая ветвь полулогарифмической кривой не доходит до ординаты, соответствующей выходу 0%, так как этому выходу по оси абсцисс соответствует  .Логарифмическая суммарная характеристика крупности строится в системе координат  , где x=l размер отверстий сита, Y - суммарный выход классов.Логарифмическая характеристика позволяет в некоторых случаях установить закономерность распределения в материале зерен по крупности. Для дробленого и измельченного материала логарифмическая характеристика, построенная «по минус l», большей частью получается прямолинейной. Пример построения логарифмической суммарной характеристики крупности (по данным табл. 4.12) показан на рис. 4.14, г. 4.2.6. Аналитическое представление характеристик крупности Гранулометрические характеристики крупности могут быть представлены в аналитической, табличной форме или графически. Интегральная характеристика f(x) представляет интегральную функцию распределения частиц крупности x; она связана с частной (дифференциальной характеристикой) F(x) соотношением  . (4.19)Наиболее общее выражение интегральной гранулометрической характеристики (функция распределения по крупности) имеет вид  , (4.20)где  - суммарный выход зерен крупности меньше размера отверстий х; х* - крупность, принятая для сравнения.Поскольку х* есть оценка некоторой средней крупности частиц, то часто ее определяют как модуль крупности. Когда уравнение включает верхний предел крупности (например, уравнение Годэна-Андреева), х* фактически представляет максимальную крупность частиц в распределении. Если уравнение не включает верхнего предела (например, уравнение Розина-Раммлера), х* обычно ближе к истинному среднему. Уравнение типа (4.20) также включает второй параметр, который может быть назван модулем распределения, поскольку он является мерой формы характеристики крупности. В некоторые уравнения включают третий параметр, связанный с асимметрией гранулометрической характеристики, но это осложняет проблему, что редко оправдывается. Некоторые наиболее общие случаи подобных (4.20) уравнений даны в табл. 4.14. Таблица 4.14 Уравнения гранулометрических характеристик крупности частиц
Если логарифмическая суммарная характеристика «по минусу» прямолинейна, то для того материала гранулометрический состав можно представить уравнением  ,где - суммарный выход класса мельче отверстий сита («по минусу»); k - коэффициент, равный тангенсу угла наклона прямой; х - размер отверстий сита;  - отрезок, отсекаемый прямой на оси ординат.Следовательно,  . (4.21)Уравнение (4.21) суммарной характеристики, построенной «по минус х», известно под названием уравнения Годэна-Андреева. Значение показателя kопределяет направление и степень изгиба кривой характеристики. Если характеристику построить «по плюс х», то она будет: при k<1 выпуклой, при k = 1 прямой, при k<1 вогнутой. Следовательно, по значению показателя kможно судить о преобладании в материале крупных или мелких зерен. Из уравнения (4.21) при х = хтах;  имеем  .Значение параметра А при данном показателе kзависит от диаметра максимального зерна материала xmax. Уравнение характеристики позволяет решать ряд задач, например определять число зерен в любом классе, поверхность зерен, удельную поверхность и т. п. Параметры уравнения находят следующим образом. На логарифмической характеристике выбирают две точки, соответствующие двум наиболее удаленным диаметрам, и определяют показатель kкак тангенс угла наклона прямой:  .Параметр А находят подстановкой значения kв уравнение (4.21) для одной из точек: 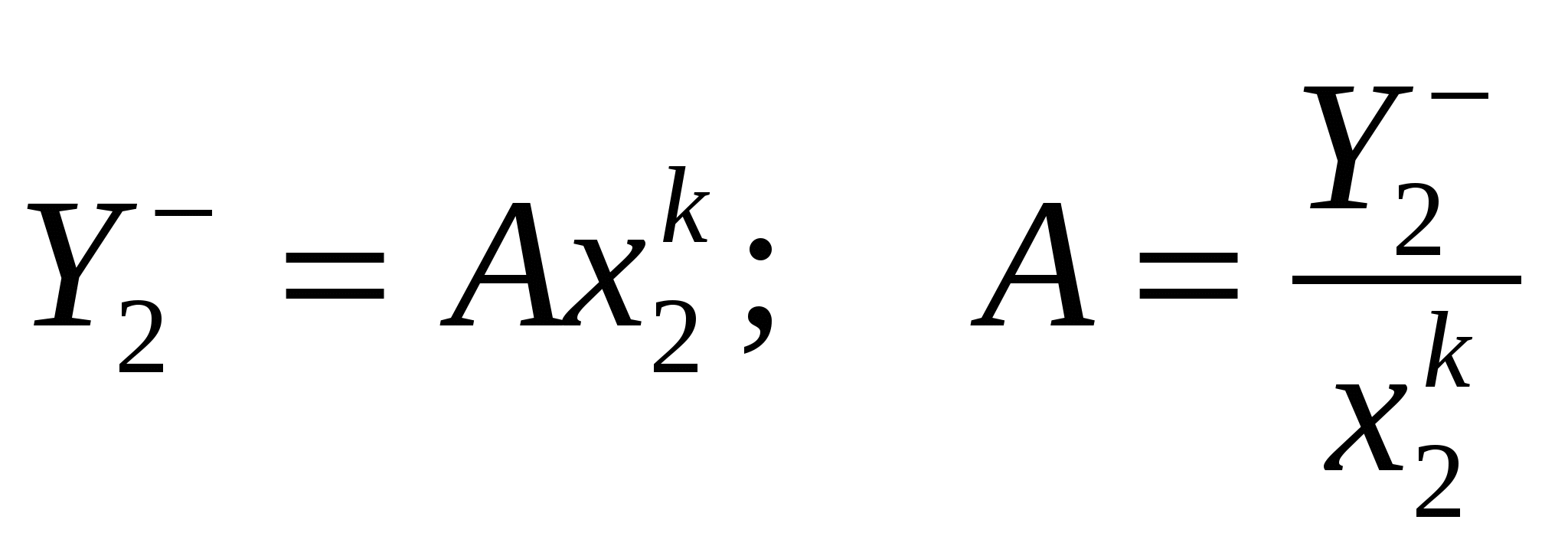 .Если диаметры зерен брать по отношению к диаметру максимального куска в материале, то уравнение Годэна-Андреева преобразуется в «приведенное» уравнение с одним постоянным параметром  или, если  выражено в долях единицы,  .Показатель kнаходят описанным выше вычислением или, если принять за исходные для расчета x2 и x1 = x2/2, то  . (4.22)Для продуктов шаровых мельниц значение показателя kв уравнениях характеристик крупности находится в пределах 0,7-1. Анализ большого числа гранулометрических анализов продуктов дробления и измельчения показала, что во многих случаях лучшее соответствие опытным данным по сравнению с уравнением Годэна-Андреева дает уравнение, предложенное Розиным и Раммлером:  , (4.23)где R - суммарный выход класса, крупнее х, по «плюсу», %; х - размер отверстий сита; bи п - параметры, зависящие от свойств материала и размерности х. Соответствие опытных данных уравнению (4.23) можно проверить графически путем нанесения опытных точек на функциональную координатную систему. При двойном последовательном логарифмировании уравнение (4.23) приобретает вид  .В координатах  уравнение Розина-Раммлера изображается прямой линией с угловым коэффициентом п. Пример построения такого графика (по данным табл. 4.12) показан на рис. 4.14, д.На осях против соответствующих логарифмических величин приведены выхода классов и диаметры зерен материала. Параметры bи п уравнения (4.23) находят по двум известным точкам, решая систему уравнений:  ; .При совместном решении этих уравнений получим 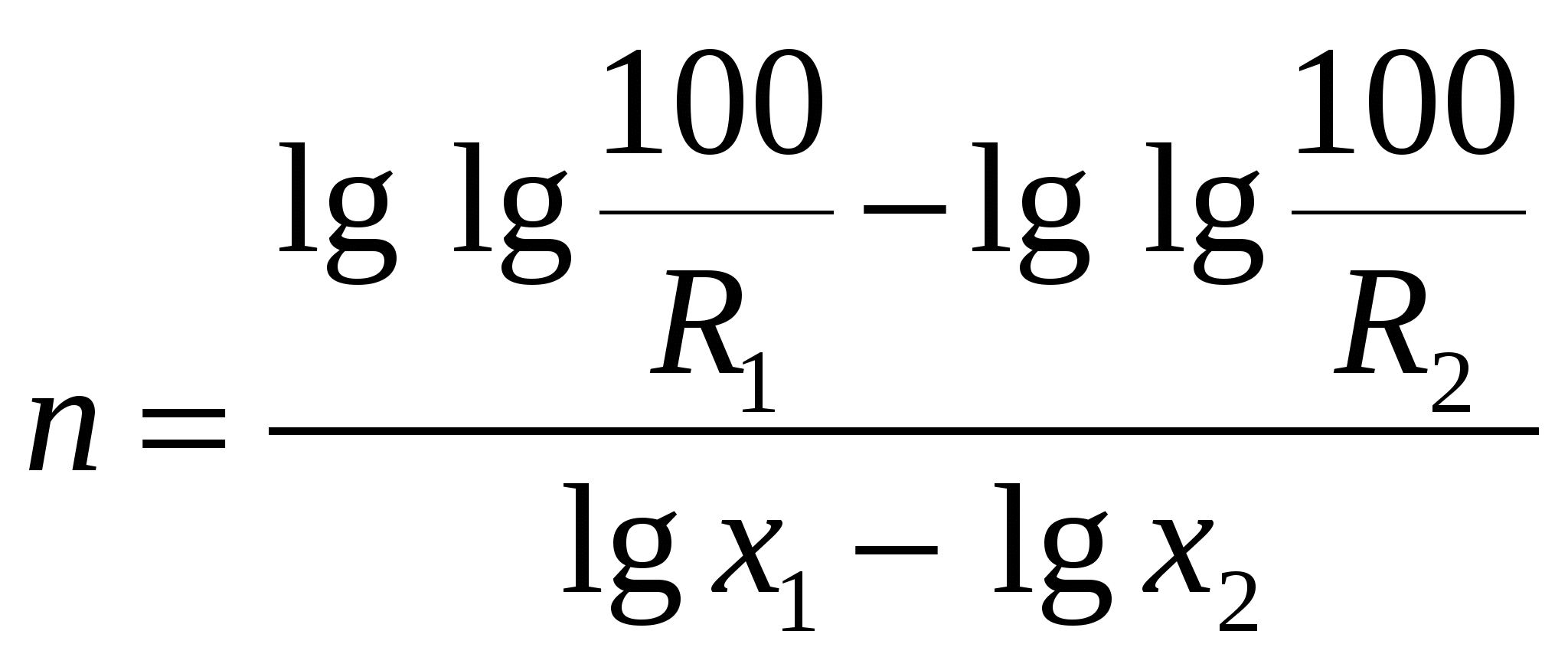 . (4.24)Зная n, определяем b: 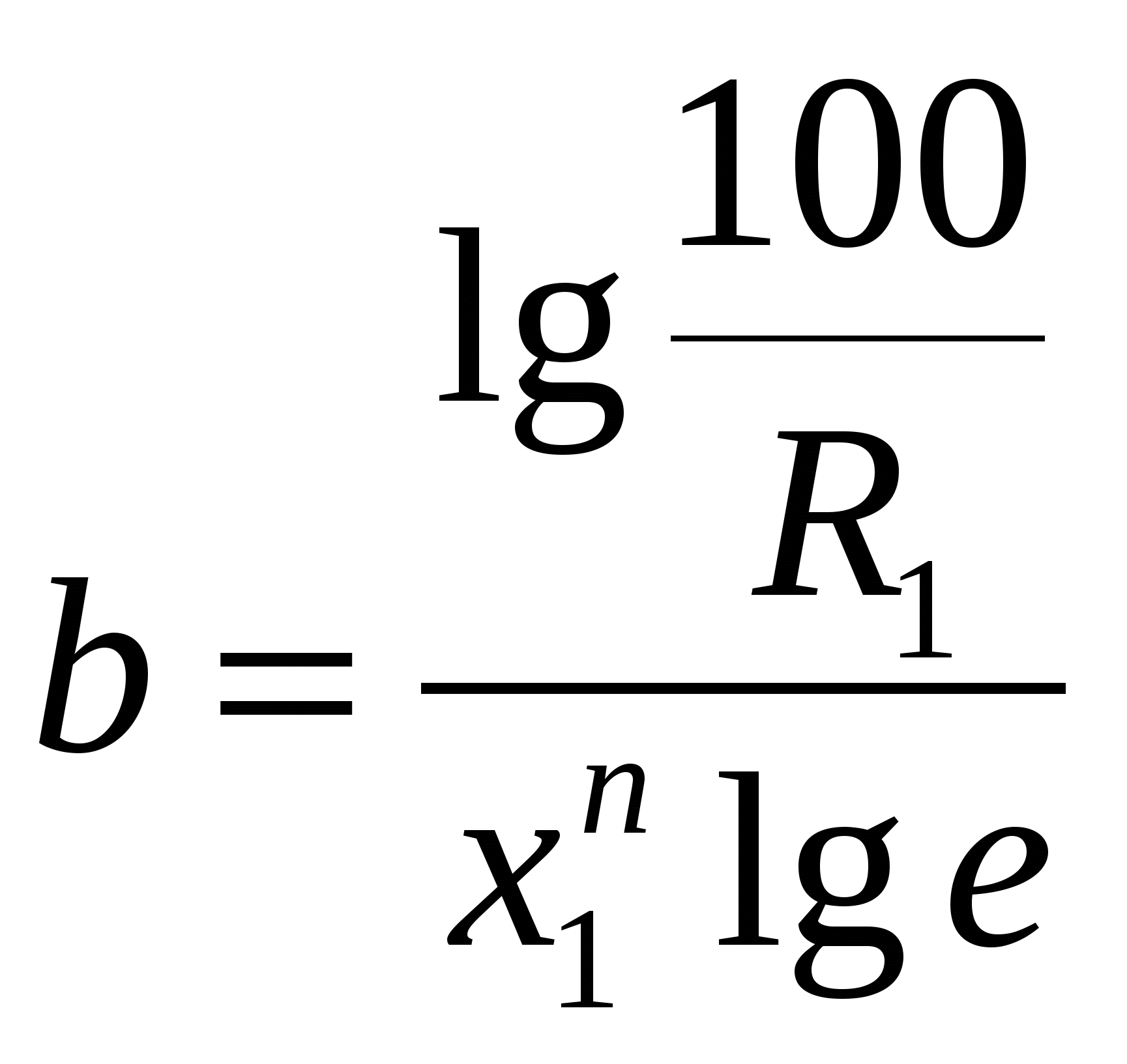 ; . (4.25)Уравнение Розина-Раммлера охватывает опытные точки в широком диапазоне крупностей, но оно не удовлетворяет одному конечному условию - нулевой выход классов достигается толькопри бесконечно большой крупности материала:  и R=0 при х = ∞.При использовании уравнения Розина-Раммлера следует учитывать это обстоятельство и принимать конечную крупность материала, соответствующую какому-то определенному значению выхода класса. Сливы классификаторов шаровых мельниц, работающих в замкнутом цикле, большей частью удовлетворяют уравнению Розина-Раммлера при п = 1. |
- среднее арифметическое; 
- стандартное отклонение
,
- крупность, при которой 
; п - константа, характеризующая исследуемый материал
