ТОЗОС часть2. Учебнометодические разработки для самостоятельной работы студентов по курсу
 Скачать 7.02 Mb. Скачать 7.02 Mb.
|
|
4.1.6. Механические свойства твердых тел при простых видах деформации Испытание твердых тел на одноосное сжатие или растяжение является основным для характеристики их прочности. С этой целью образцы цилиндрической формы или прямоугольного сечения нагружаются на испытательном прессе до разрушения. В табл. 4.1 приведен ряд механических параметров твердых тел, в табл. 4.2 рассмотрены свойства некоторых твердых тел. Таблица 4.1 Механические параметры твердых тел
Примечание. F- площадь поперечного сечения образца, м2; l, d - длина и диаметр образца, м; d и l - изменение диаметра и длины образца, соответствующие изменению нагрузки на величину Р, м; Pmax - максимальная нагрузка, Н. Таблица 4.2 Физико-механические свойства природных материалов
Экспериментально установлено, что при одноосном сжатии большинства твердых тел наблюдается течение материала (т. е. пластическая деформация) перед началом разрушения. Показатели механических свойств твердых тел зависят от их состава и строения. Силы сцепления между кристаллитами, цементирующим веществом и обломками, кристаллитами цементирующего вещества колеблются в широких пределах, что обусловливает большие колебания в механических свойствах твердых тел. На показатели влияет способ испытаний, пористость, влажность, слоистость, крупность слагающих твердое вещество частиц и др. Этими причинами объясняется широкий разброс показателей при испытаниях образцов одного и того же материала, не отличающихся один от другого по петрографическому описанию. Например, специальные исследования образцов одинаковых природных материалов на одноосное сжатие показал, что временное сопротивление сжатию изменилось в 8,45 раза (от 530 до 1830 кПа) и средний коэффициент вариации (отношение средне квадратичного отклонения к среднему значению) был равен 21,3%. Были проведены на микроаппаратуре опыты по разрушению сжатием малых по размерам частиц (шаров) стекол и природных материалов. При этом было установлено, что чем меньше размер разрушаемой частицы, тем больше пластическая деформация, предшествующая разрушению. Для очень мелких частиц имеется предел размера, ниже которого возникает только пластическая деформация. Для кварца он составляет около 1 мкм, для полевого шпата - 3-5 мкм (практический предел механического разрушения частиц). Испытание природных материалов на растяжение производится редко, главным образом из-за трудности изготовления образцов. Испытание на разрыв весьма чувствительно к неоднородности материала и мелким дефектам его строения (микротрещины). Сопротивление разрыву природных материалов в несколько раз меньше по сравнению с временным сопротивлением сжатию. Отношение Испытания природных твердых материалов на сдвиг и изгиб проводятся только при специальных исследованиях. Прочность на сдвиг выше, чем прочность на изгиб и растяжение (разрыв): где σсж, с, σи, σр, - временное сопротивление соответственно на сжатие, изгиб, растяжение и сдвиг. В табл.4.3 приведены данные об относительной прочности природных материалов при разных видах напряжений. Как следует из таблицы, энергически наиболее выгодным видом деформации для разрушения материала является растяжение. Это необходимо иметь в виду при конструировании дробильно-измельчительного оборудования. Таблица 4.3 Относительная прочность (%) природных материалов при разных видах напряжений
Многочисленными испытаниями прочностных свойств природных материалов установлена высокая степень изменения экспериментальных показателей даже для образцов одного и того же природного материала и зависимость их от многих факторов, которые в настоящее время не поддаются количественной оценке. Анизотропные свойства природных материалов. Анизотропными называют тела, обладающие различными свойствами в разных направлениях. Анизотропия природных материалов связана с их слоистостью, сланце- и трещиноватостью. С увеличением трещиноватости степень анизотропии понижается. Практически об анизотропии прочности природных материалов судят по показателям прочности, определенным поперек (перпендикулярно) и вдоль слоистости. Отношение показателя свойства поперек слоистости к показателю того же свойства вдоль слоистости называется коэффициентом относительной анизотропии свойств. Коэффициент анизотропии на сжатие для многих природных материалов в среднем равен 1,34. Для показателей временного сопротивления растяжению (отрыву) коэффициент анизотропии составляет в среднем 0,59, т. е. сопротивление перпендикулярно к слоистости меньше. Масштабный фактор. Согласно статистической теории прочности, дефекты в строении твердого тела распространены в объеме стохастически. Чем больше объем нагружаемого куска, тем выше вероятность наличия в нем с крупного дефекта, достаточного для разрушения куска по всему сечению при данной нагрузке. С уменьшением размера кусков в них уменьшается число больших дефектов, (поскольку были уже реализованы при разрушении до данного размера), удельная прочность кусков повышается. Зависимость прочности твердых тел от их линейных размеров называют масштабным эффектом или масштабным фактором. Большая часть экспериментов подтверждает положение, что образцы (куски) материала меньших размеров, при прочих равных условиях обладают большей удельной прочностью по сравнению с кусками больших размеров. Для природных материалов наблюдается заметное увеличение прочности частиц размером 0,1 ÷ 0,5 мм. Особенное значение масштабный фактор имеет для природных материалов, в которых частицы одного твердого материала связаны (сцементированы) более мягким связующим материалом. В этом случае разрушение до необходимого размера частиц измельчаемого материала проходит относительно легче, чем разрушение самих твердых частиц. Природные материалы настолько разнообразны по своему составу и свойствам, что в некоторых случаях наблюдается обратное влияние масштабного фактора, т. е. удельная прочность кусков возрастает с увеличением их размеров. Поэтому влияние масштабного фактора должно изучаться применительно к конкретному природному материалу и к определенному диапазону крупностей кусков. Твердость природного материала определяет ее сопротивляемость к внедрению инструмента. Простой способ определения твердости, так называемой контактной прочности, разработан в Институте горного дела. В нешлифованную поверхность куска природного материала вдавливают стальной цилиндрический штамп с плоским основанием диаметром 2÷3 мм. Контактная прочность определяется в момент выкола лунки по нагрузке, отнесенной к площади штампа, т. е. она измеряется в ньютонах на 1 мм2. К самым твердым относят материалы, имеющие контактную прочность более 5,66 Н/мм2, к материалам средней твердости - 0,65÷1,25 кН/мм и к слабым - менее 0,3 кН/мм2. Общий коэффициент крепости природного материала. Вследствие большой изменчивости показателей свойств материала и зависимости их от технологических процессов, для которых они определяются, в практике нашли применение частные показатели свойств, характерные для определенных процессов. Так, выработаны показатели буримости, взрываемости, дробимости, абразивности, измельчаемости природного материала и др. Общая методика разработки частных показателей, характерных для данного технологического процесса, следующая. Процесс моделируют (воспроизводят) в малом масштабе, изготовляют специальную аппаратуру и приборы, на которых определяют показатели на отдельных пробах. Эти показатели сопоставляются с показателями промышленных установок и выявляются корреляционные зависимости между ними. После этого показатель, полученный при испытаниях пробы, можно использовать для расчета промышленных установок и проектирования технологического процесса. Для характеристики прочностных свойств природных материалов существует общий показатель) крепости. Этот коэффициент крепости обоснован многолетней практикой, и специальными испытаниями и хотя по точности он не может заменить частных показателей, применяемых к конкретным процессам, его можно использовать для общего сравнения прочности природных материалов в разных отраслях промышленности и для разных процессов при ориентировочных расчетах. По шкале проф. М. М. Протодьяконова все природные материалы делятся на 10 категорий, характеризуемых коэффициентами крепости от 0,3 для самых слабых, плывучих грунтов до 20 для наиболее прочных и вязких кварцитов и базальтов. Коэффициент крепости f, как показали исследования, можно приближенно определить по временному сопротивлению раздавливанию σсж цилиндрического образца (d= h = 32÷42 мм) по формуле 4.1.7. Законы дробления Под законами дробления понимается зависимость между затраченной на дробление энергией (работой) и крупностью продукта, получаемого в результате дробления (измельчения). Общее выражение эмпирической зависимости, характеризующей энергетические затраты на сокращение крупности, может быть представлено в виде где Е - удельная энергия, сообщаемая единице объема разрушенного тела, необходимая для прироста энергии вновь образованной поверхности; k - коэффициент пропорциональности; х - средний диаметр зерен; f(x) - показатель степени, зависящий от крупности частиц. Дифференциальное уравнение (4.8) может быть представлено в более простой форме: где п - коэффициент, который зависит от диапазона крупности и способа дробления (измельчения). На рис.4.2 показана графическая интерпретация выражения (9). Эта зависимость есть обобщенная форма теоретических и эмпирических уравнений Риттингера, Кика, Кирпичева, Бонда, Свенссона, Холмса и других авторов. Наиболее известными являются уравнения Риттингера, Кика-Кирпичева, Бонда, которые принято называть «законами». Первые два «закона» (Риттингера и Кика-Кирпичева) имеют теоретическую основу, но они не применимы для всего диапазона крупностей. Третий закон (Бонда) является чисто эмпирической зависимостью, выведенной из анализа результатов периодического измельчения большого числа руд. 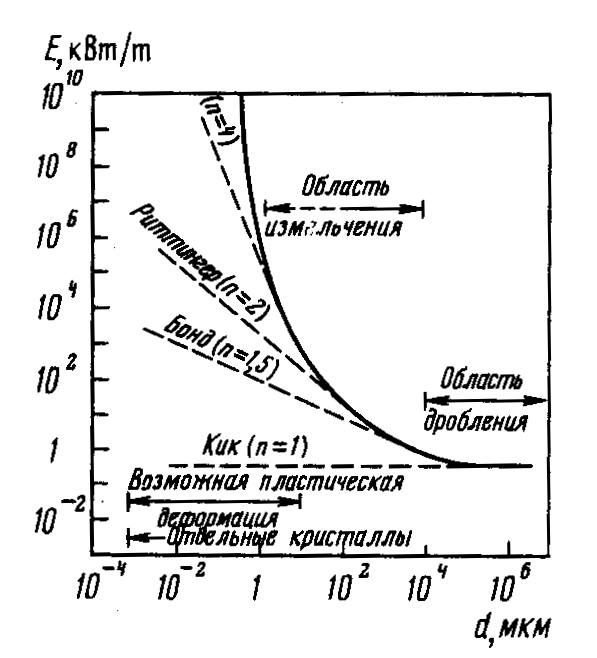 Рис. 4.2. Зависимость удельного расхода энергии Е от крупности разрушаемых частиц П. Риттингер (1867) установил, что энергия разрушения пропорциональна вновь образованной поверхности где Sн, Sк - поверхность материала до и после разрушения, м2; k1- коэффициент пропорциональности, Дж/м2. Это уравнение может быть получено путем интегрирования уравнения (4.9) при п = 2: где Dср и dср - средняя крупность частиц соответственно исходного и дробленого продукта. Закон дробления Кика–Кирпичева (1874, 1875) гласит: подобным деформациям геометрически подобных и физически одинаковых тел соответствуют работы, пропорциональные объемам тел: где kv - коэффициент пропорциональности, Дж/м3; V- объем кубического куска с ребром D, м. Уравнение (4.12) может быть получено также из (4.9) интегрированием его в тех же пределах при п = 1 где i- степень сокращения. В результате обработки данных многочисленных серий опытов, охватывающих широкий диапазон природных материалов, Бонд (1951) установил, что Общий вид уравнения, используемого Бондом, где D80 и d80 - размер отверстий сита, через которые проходит 80% материала соответственно до и после дробления. Уравнения (4.14) и (4.15) могут быть получены из (9) при интегрировании для n= 1,5. Выражение (4.15) широко используется в зарубежной практике для выбора дробилок. В работах Бонда и каталогах фирмы «Аллис-Чалмерс» подобная формула также рекомендуется для определения производительности (кВтч/т) дробилок: где N1 - мощность приводного двигателя рассчитываемой дробилки, кВт; Q1 - производительность рассчитываемой дробилки, т/ч; W1, - индекс работы но Бонду. Индексом работы W1(табл. 4.4) Бонд называет удельный расход энергии в киловатт-часах на одну короткую тонну (короткая тонна - единица измерения массы, принятая в США, равна 0,907 метрической тонны), необходимый для дробления от бесконечного массива до продукта крупностью 80 % - 100 мкм. Таблица 4.4 Индекс работы для некоторых полезных ископаемых, определенный Бондом опытным путем
Работу дробления 1 т материала от бесконечного массива Dср = ∞ до продукта 80% - 100 мкм (dср = 100 мкм2) можно представить в виде и индекс работы Для определения производительности дробилки необходимо мощность приводного электродвигателя дробилки разделить на удельный расход энергии, вычисленный по формуле (4.16). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
