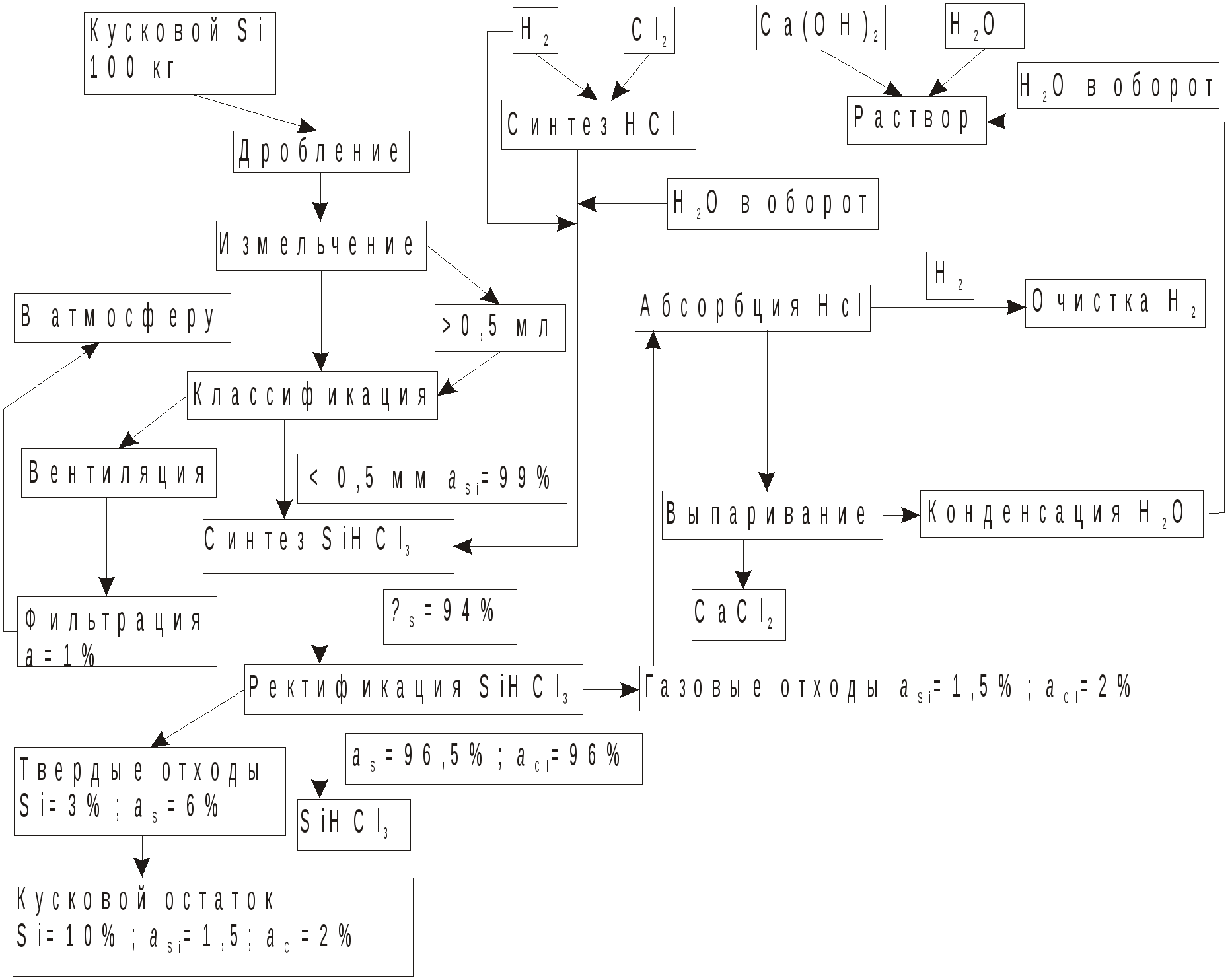|
|
ТОЗОС часть2. Учебнометодические разработки для самостоятельной работы студентов по курсу
Примеры выполнения домашних заданий
Пример выполнения домашнего задания №1.
Почему скорость осаждения частиц в суспензиях различной плотности различна?
Решение:
Как известно при отстаивании сточных вод наблюдается стесненное осаждение, которое сопровождается столкновением частиц, трением между ними и изменением скоростей как больших, так и малых частиц. Скорость стесненного осаждения меньше скорости осаждения свободно осаждающихся частиц вследствие возникновения восходящего потока жидкости и большой вязкости среды.
Предположим, что частицы шарообразны. В противном случае необходимо делать поправку на форму частиц.
Скорость стесненного осаждения шарообразных частиц одинакового размера можно рассчитать при ламинарном режиме течения жидкости по формуле Стокса с поправочным коэффициентом, который учитывает влияние концентрации взвешенных частиц и реологические свойства системы
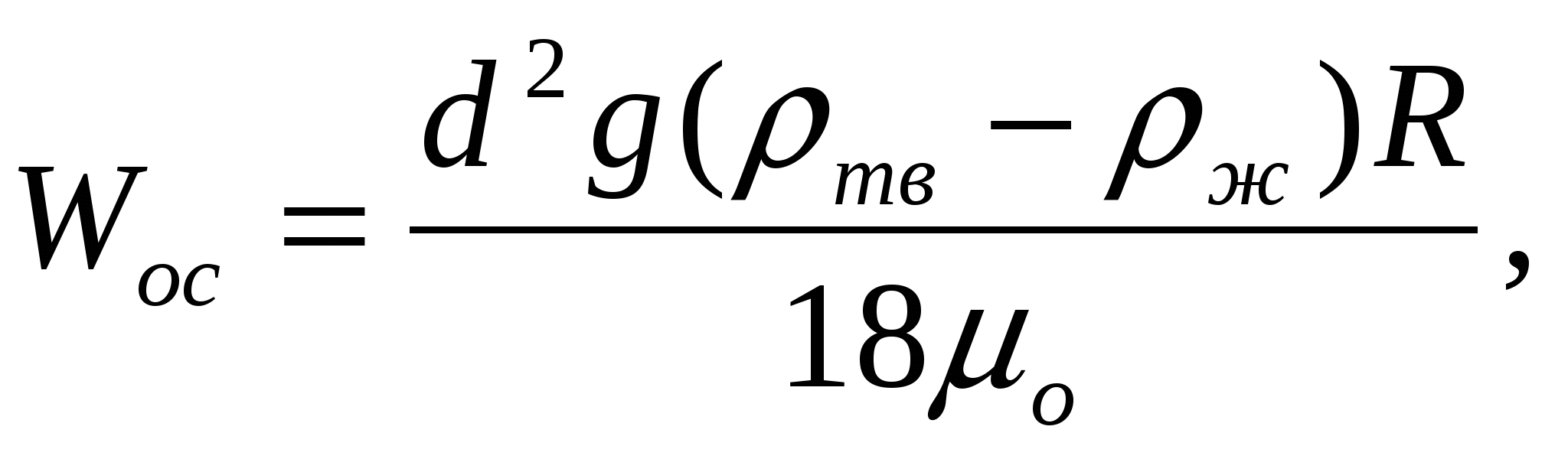 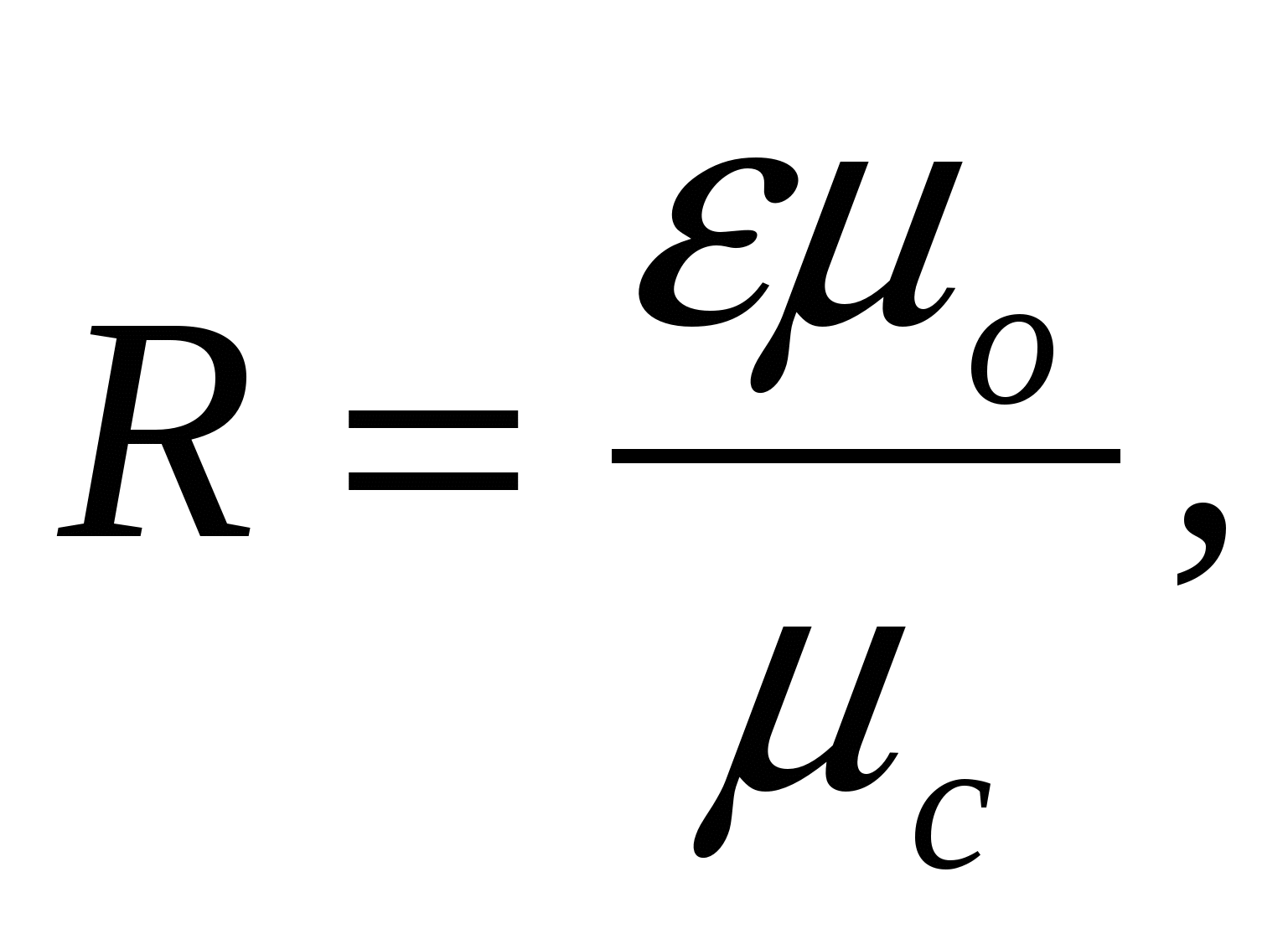
где ε - объемная доля жидкой фазы, 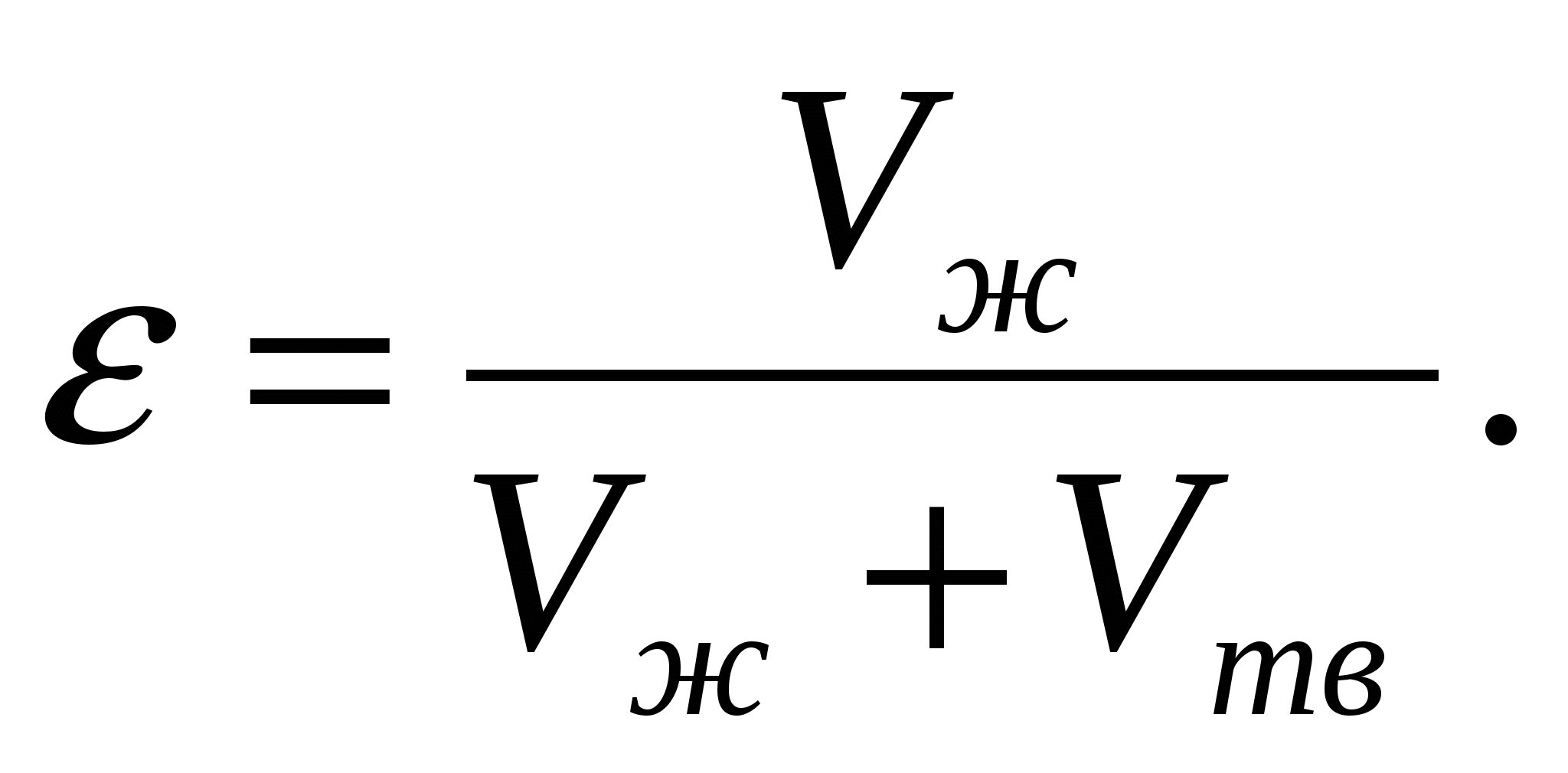
Как видно из формулы Стокса Wос - скорость осаждения частиц - прямо пропорциональна разнице плотностей (ρтв–ρж) и, чем больше эта разность, тем больше скорость осаждения. Из данной формулы видно, что если в суспензии плотность частиц ее образующих различна, то, следовательно, будет различна и скорость осаждения этих частиц.
Пример выполнения домашнего задания №2.
Что такое краевой угол смачивания?
Решение:
На границе соприкосновения трех фаз (1 - жидкость, 2 - газ, 3 - твердое тело) наблюдается явление называемое смачиванием (см. рис.). Свободная поверхность жидкости около твердой поверхности искривлена и называется мениском. Линия, по которой мениск пересекается с твердым телом, называется периметром смачивания.
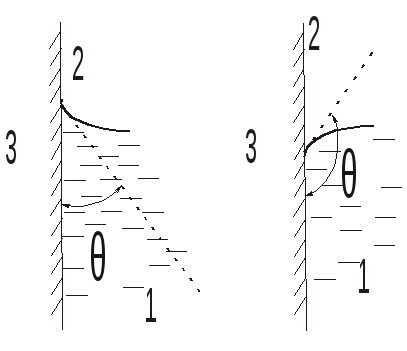
Рис. Краевой угол смачивания
Явление смачивания характеризуется краевым углом смачивания θ, который образуется между смоченной поверхностью твердого тела и мениском в точках их пересечения (периметра смачивания). Мерой смачивания считается величина cosθ, определяемая по уравнению Юнга
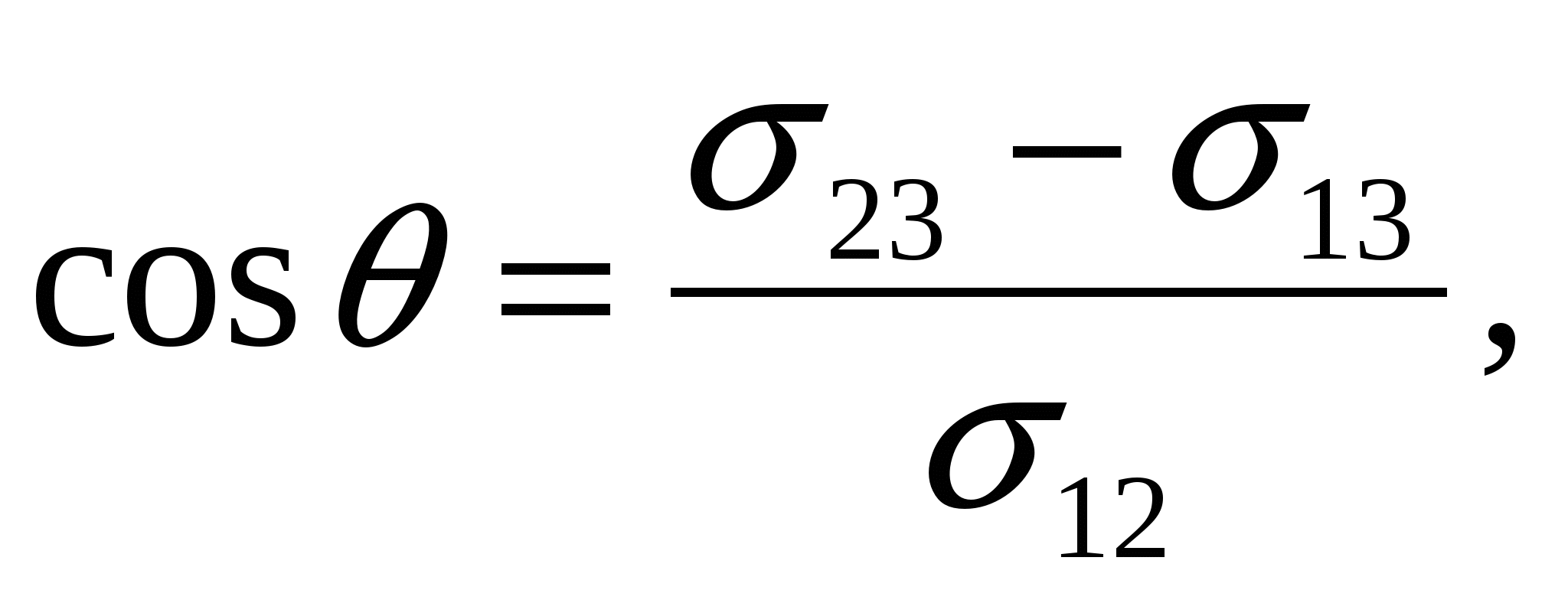
где σik - поверхностное натяжение на трех поверхностях раздела. Если σ23 > σ13, то θ < π/2. В этом случае жидкость имеет вогнутый мениск и смачивает твердое тело. Такая поверхность называется гидрофильной. Если σ23 < σ13, то θ > π/2. Жидкость имеет выгнутый мениск и не смачивает твердое тело. Эта поверхность называется гидрофобной. Если σ23–σ13→σ12, то θ→0. Мениск касателен к поверхности твердого тела (идеальное смачивание). Межмолекулярные силы, действующие на частицу поверхностного слоя, в этом случае полностью компенсированы, и свободная поверхностная энергия этого слоя имеет минимальное значение. Если σ23→σ12, то θ→π/2. Жидкость имеет плоскую свободную поверхность. В этом случае смачивание и несмачивание отсутствуют.
Темы заданий для курсовых работ по курсу «Теоретические основы защиты окружающей среды»
Составить технологическую схему реального технологического процесса, на основе которой провести расчет материального и энергетического баланса реального технологического процесса.
Порядок выполнения курсовой работы:
выбрать по согласованию с преподавателем реальный технологический процесс, применяемый в микроэлектронике и электронной технике;
составить качественную технологическую схему выбранного процесса (если с участием жидкой фазы, то вместо качественной технологической схемы составить шламовую схему процесса), на которой указать выход продукта в том или ином агрегатном состоянии на той или иной технологической операции с указанием возможных технологических потерь продукта;
провести расчет материального и энергетического балансов конкретного технологического процесса, используя современную классификацию процессов химической технологии:
гидромеханические процессы;
тепловые процессы;
массообменные процессы;
механические процессы;
химические процессы, связанные с превращением вещества;
на основе проведенных расчетов материального и энергетического балансов разрабатывается количественная схема избранного технологического процесса.
Пример выполнения курсовой работы
Материальный и энергетический балансы
Для правильного выбора способов очистки окружающей среды от отходов производства необходимо, прежде всего, провести анализ возможности возникновения отходов в реальном процессе и составить уравнение материального баланса.
Например, для изготовления эпитаксиальных кремниевых пластин широко используется водородное восстановление трихлорсилана по уравнению:
2SiHCl3(г)+2H2(г)2Si(тв)+6HCl.
Рассмотрим процесс получения трихлорсилана и составим схему материального баланса производства. Трихлорсилан - это бесцветная дымящаяся и легкозагорающаяся на воздухе жидкость плотностью 1,35 г/см3, кипящая при 31,8 °С и кристаллизирующаяся при –127 °С.
Для получения трихлорсилана производится обработка технического кремния хлористым водородом:
Si(тв)+3HCl(ж)=SiHCl3(г)+H2(г).
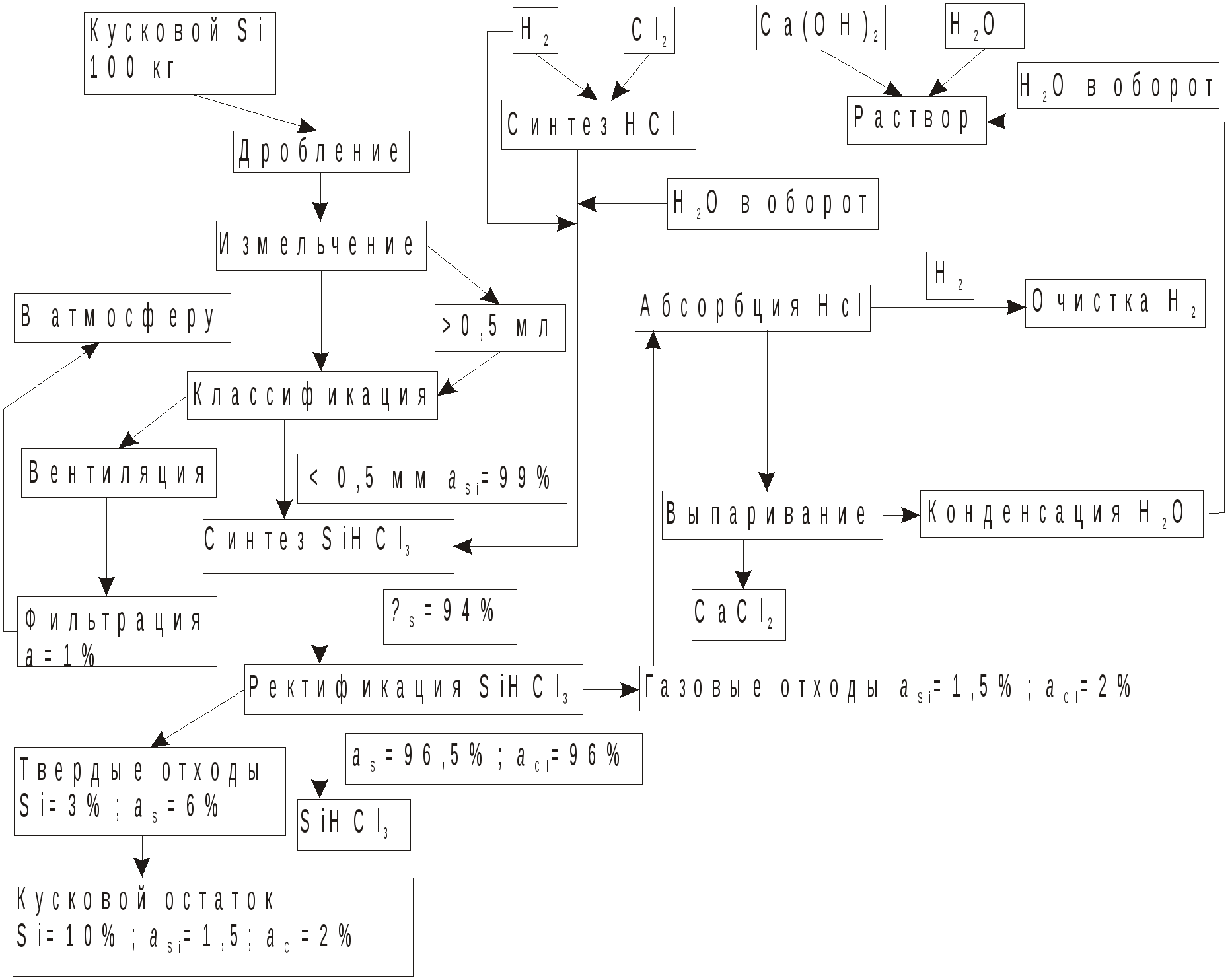
Рис. 1. Общая схема получения трихлорсилана
Реакция проводится обычно при температуре 300 400 °С с использованием измельченного кремния. Выход трихлорсилана возрастает при добавлении к хлористому водороду чистого водорода.
Очень важна хорошая очистка поступающей газовой смеси от кислорода и водяного пара, присутствие которых вызывает осаждение продуктов реакции гидролиза на кремний и снижение его реакционной способности.
Общая по этапам схема получения трихлорсилана с учетом потерь α на каждой операции приведена на рис. 1 продуктов реакции, например, получения 100 кг кремния в табл.1 расчет по уравнениям (1.1) и (1.2).
Таблица 1.
Материальный баланс процесса получения трихлорсилана (из 100 кг Si)
Наименование
|
Количество, кг
|
Si
|
Cl
|
%
|
кг
|
%
|
кг
|
1. Трихлорсилан
|
428
|
21
|
89,81
|
78,3
|
335
|
2. Твердые отходы синтеза
|
19,8
|
30
|
5,94
|
|
|
3. Кубовой остаток ректификации
|
13,9
|
10
|
1,39
|
|
|
4. Газы при ректификации
|
93,0
|
2
|
1,86
|
|
|
Итого:
|
|
|
100
|
|
|
Материальный баланс
Для получения трихлорсилана производится обработка 100 кг технического кремния хлористым водородом:
Si(тв)+3HCl(ж)=SiHCl3(г)+H2(г).
Первоначально из 100 кг кускового кремния на фильтрацию тратится 1%, т.е.:
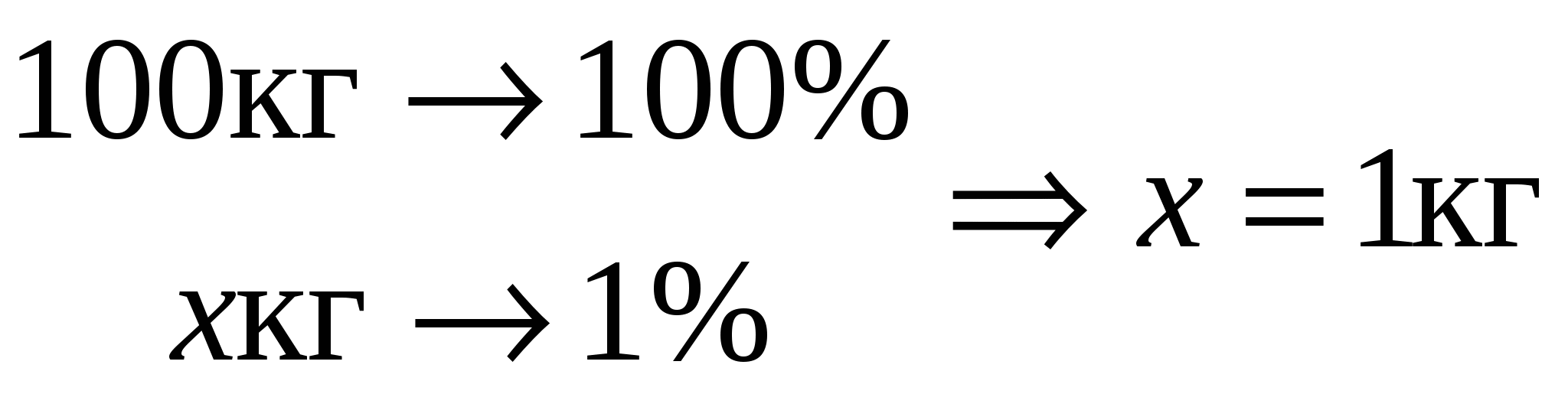 . .
На синтез SiHCl3 поступает (100 – 1) = 99 кг кремния. Из них, на твердые отходы синтеза теряется 6%, т.е.
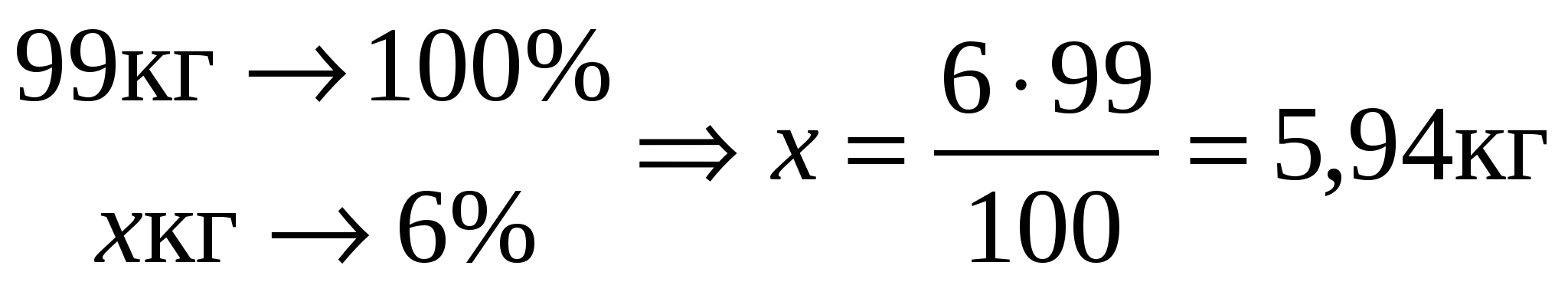 . .
Оставшиеся (99 – 5,94) = 93,06 кг поступает на ректификацию, где 2% кремния расходуется на газовые отходы, т.е.
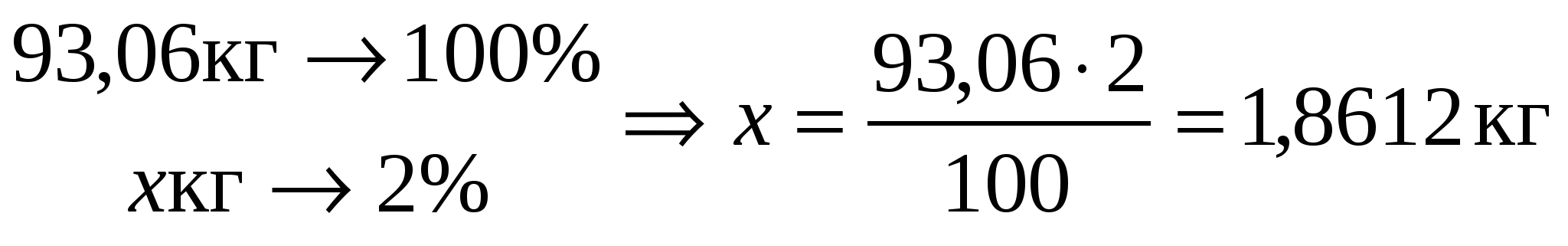 , ,
а 1,5% - на кусковой остаток, т.е.
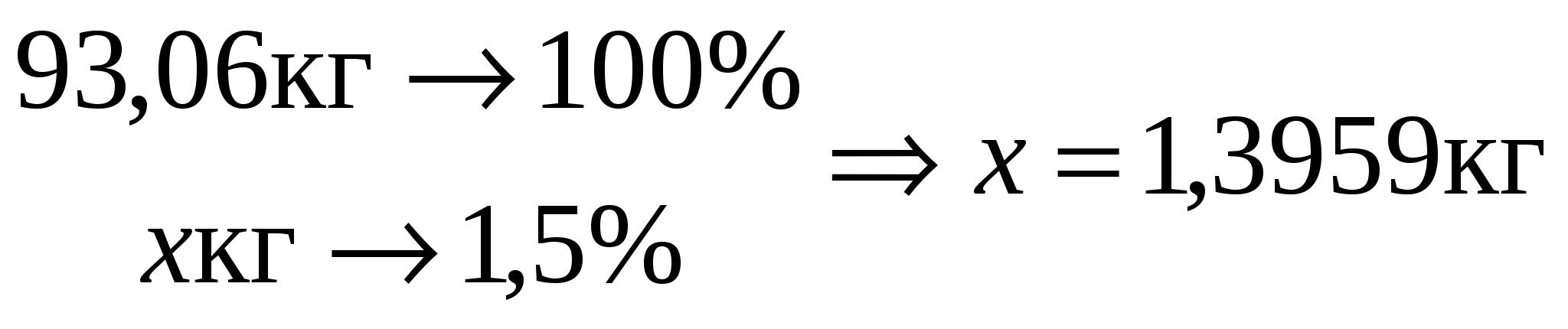 . .
Следовательно, масса кремния в полученном трихлорсилане составляет (93,06 – 1,8612 – 1,3959) = 89,8 кг.
Таблица 2.
Наименование
|
Количество, кг
|
Si
|
Cl
|
%
|
кг
|
%
|
кг
|
1
|
2
|
3
|
4
|
5
|
6
|
1. Трихлорсилан
|
428
|
21
|
89,8
|
78,3
|
335
|
1
|
2
|
3
|
4
|
5
|
6
|
2. Твердые отходы синтеза
|
19,8
|
30
|
5,94
|
-
|
-
|
3. Кубовой остаток ректификации
|
13,9
|
10
|
1,396
|
50,22
|
6,98
|
4. Газы при ректификации
|
93,0
|
2
|
1,86
|
7,5
|
6,98
|
Итого:
|
|
|
100
|
|
348,96
|
По таблице 1 масса хлора в трихлорсилане равна 335 кг, что составляет 96% от первоначальной массы хлора, т.е.
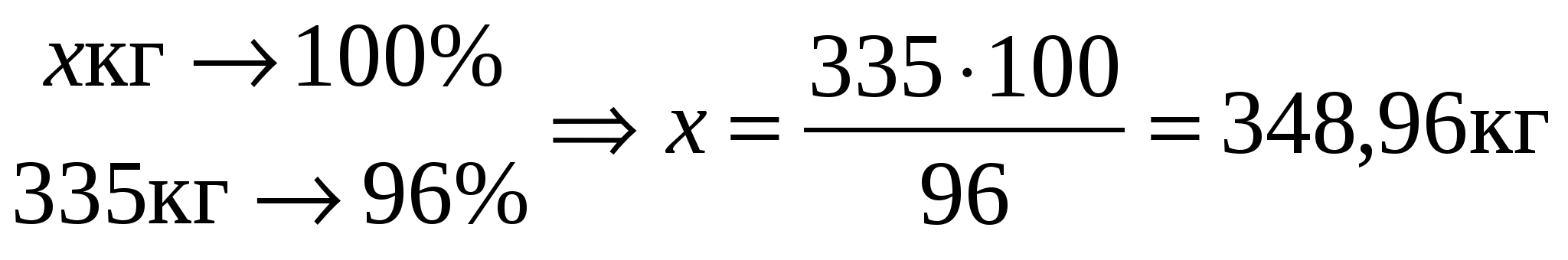 . .
Из них 2% составляет кусковой остаток, т.е.
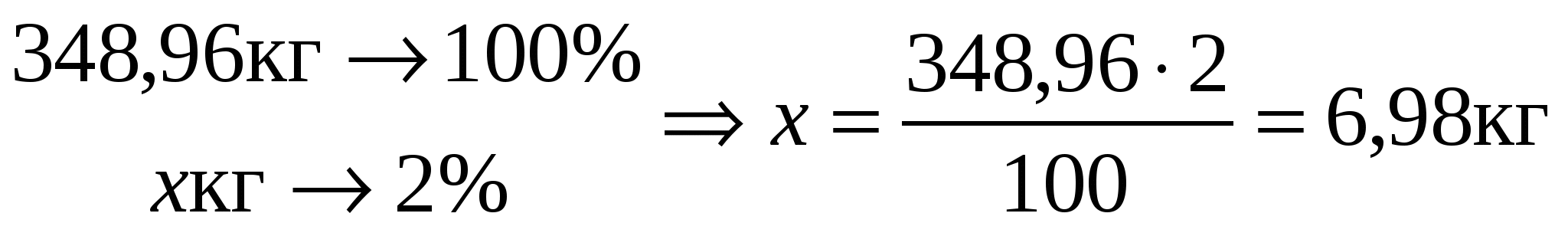 . .
и 2% (6,98 кг) - газовый отходы при ректификации. Рассчитаем процентное содержание хлора (для табл.1) в кубовом остатке ректификации:
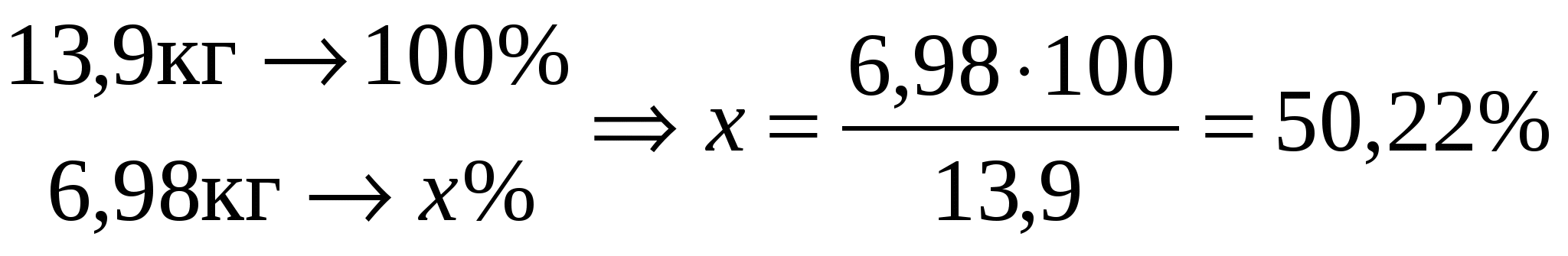 , ,
в газах при ректификации:
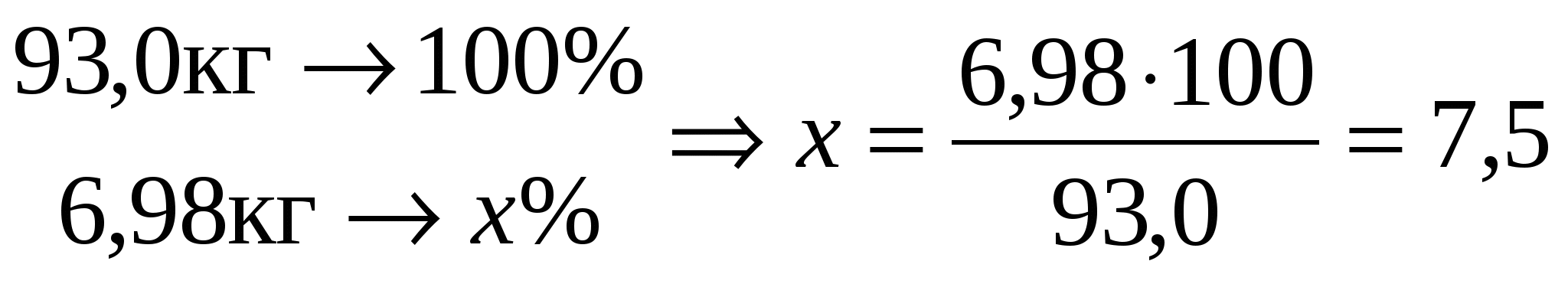 кг. кг.
Энергетический баланс
Таблица 3.
Элемент (вещество)
|
H0298 кДж/моль
|
S0298 Дж/мольК
|
G0298 кДж/моль
|
T, К интервал температур
|
Si(тв)
|
0
|
18,83
|
0
|
298-1685
|
HCl(ж)
|
-92,31
|
186,79
|
-95,30
|
298-2000
|
SiHCl3(г)
|
-657,52
|
330,95
|
-617,62
|
298-1000
|
H2(г)
|
0
|
130,50
|
0
|
298-3000
|
m (кг) 100 428
Si(тв)+3HCl(ж)=SiHCl3(г)+H2(г)
М (г/моль) 28,1 36,51 135,61 2,02
Масса трихлорсилана:
m(SiHCl3) = m(Si)+m(H)+m(Cl3) => m(H) = 428 – 89,81 – 335 = 3,19 кг
Т.к. потерь водорода в реакции нет, то масса выделившегося водорода:
m(H2)=3,19∙2 = 6,38 кг.
Следовательно, m(HCl) = 3[m(H) + m(Cl)] = 3∙(3,19 + 335/3) = 344,5 кг.
Количество вещества:
ν(Si) = 100/28,1 = 3,559 моль,
ν(HCl) = 344,5/36,51 = 9,436 моль,
ν(SiHCl3) = 428/135,61 = 3,156 моль,
ν(H2) = 6,38/2,02 = 3,158 моль.
Энтальпия реакции:

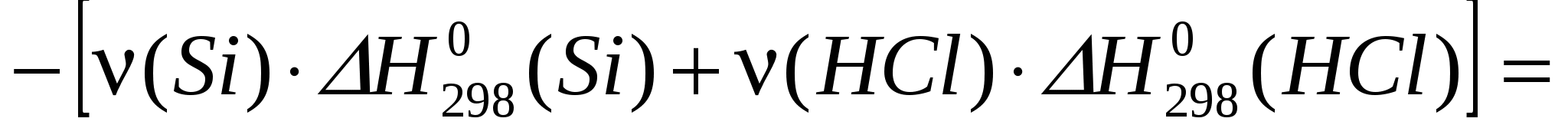
= 3,156∙(–657,52) – 9,436∙(–92,31) = –2075,133 + 871,037 =
= –1204,096 кДж/моль
Энтропия реакции:

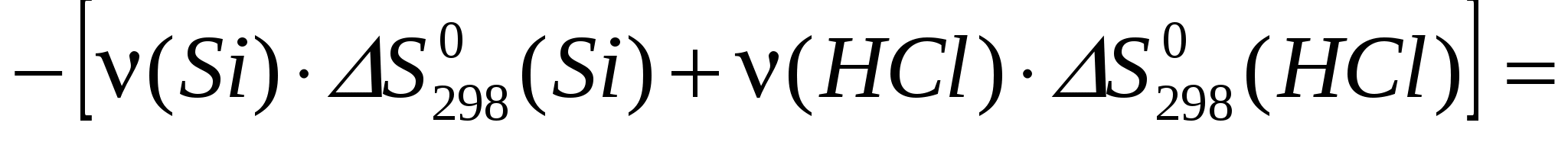
= [3,156∙330,95 + 3,158∙130,50] – [9,436∙186,79 + 3,559∙18,83] =
=1456,5972 – 1829,5663 = –372,9691 Дж/моль∙К.
Свободная энергия Гиббса:

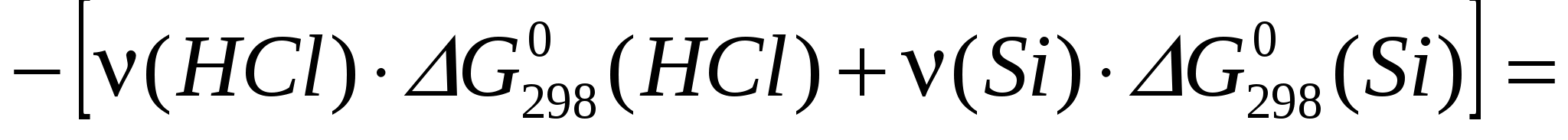
= 3,156∙(–617,62) – 9,436∙(–95,30) = –1049,9579 кДж/моль.
Вывод:
Т.к. энтальпия данной реакции ΔH < 0, то, следовательно, реакция получения трихлорсилана является экзотермической, т.е. протекает с выделением тепла. Т.к. энтропия реакции ΔS < 0, то, следовательно, данный процесс обратим. Т.к. свободная энергия Гиббса так же ΔG < 0, то это свидетельствует о том, что данная реакция идет.
Тесты
Порядок выдачи вопросов теста: в случайном порядке.
Считать вес каждого вопроса равным единице.
В математической форме первое начало термодинамики записывается как:
Q = ΔU + A.
Q = ΔU.
Q = A.
Q = ΔU +Δ A.
Q = ΔU – A.
Какое выражение первого начала термодинамики является правильным, если работа совершается самой системой:
Q = ΔU + A.
Q = ΔU.
Q = A.
Q = ΔU +Δ A.
Q = ΔU – A.
Какое выражение первого начала термодинамики является правильным, если работа совершается за счет внешних сил над системой:
Q = ΔU + A.
Q = ΔU.
Q = A.
Q = ΔU +Δ A.
Q = ΔU – A.
В дифференциальной форме уравнение первого начала термодинамики записывается:
δQ = δU + δA.
δQ = dU + δA.
δQ = dU + dA.
dQ = dU +dA.
dQ = δU – dA.
Какое выражение из ниже перечисленных, с точки зрения энтропии, является критерием обратимости процесса в идеальной системе:
ΔS = 0.
ΔS > 0.
ΔS < 0.
ΔS ≥ 0.
ΔS ≤ 0.
Какое выражение из ниже перечисленных с точки зрения энтропии является критерием необратимости процесса в идеальной замкнутой системе:
ΔS = 0.
ΔS > 0.
ΔS < 0.
ΔS ≥ 0.
ΔS ≤ 0.
С учетом первого начала термодинамики дифференциальное уравнение энтропии имеет вид:
dS = 1/T (dU + pdV).
ΔS = 1/T (ΔU + pdV).
ΔS = 1/T (δU + pδV).
dS = 1/T (ΔU + ΔpΔV).
ΔS = 1/T (dU + ΔpΔV).
Энтропия системы при стремлении температуры к абсолютному нулю стремится к
0.
∞.
к конечной величине.
к отрицательной величине.
к положительной величине.
Укажите выражение, связывающие энтропию с вероятностью осуществления данного макроскопического состояния
S = k lnΩ (ε, N).
S = R ln Ω(ε, N).
S = k lnΩ(N).
S = k ln Ω(ε).
S = R lnΩ(N).
S = R lnΩ(ε).
В термодинамике неравновесных процессов баланса энтропии записывается:
– ρdS/dt = – div Is + σ.
ρdS/dt = div Is + σ.
ρdS/dt = – div Is + σ.
ρdS/dt = – div Is – σ.
– ρdS/dt = div Is + σ.
Информационная энтропия равна:
n
H = -∑Pk lnPk при ∑Pk=0.
k=1 к=1
∞
H = -∑Pk lnPk при ∑Pk=1.
k=1 к=1
∞
H = ∑Pk lnPk при ∑Pk=1.
k=1 к=1
n n
H = -∑Pk lnPk при ∑Pk=0.
k=1 к=1
∞ ∞
H = ∑Pk lnPk при ∑Pk=0.
k=1 к=1
В статистической физике энтропия системы, состоящей из N частиц, описывается уравнением:
S = Kб ln Ω.
S = T ln Ω.S = R ln Ω.
S = KбT ln Ω.
S = RT ln Ω, где Ω - плотность состояний или статистический вес.
Энтропия системы обладает свойством:
неаддитивности.
аддитивности.
скачкообразности.
плавно изменяется.
равна нулю.
Если система приходит в состояние разупорядочения, то полная энтропия системы равна:
ΔSраз = ΔSпоз – ΔSкол + ΔSэл.
ΔSраз = ΔSпоз + ΔSкол + ΔSэл.
ΔSраз = - ΔSпоз + ΔSкол + ΔSэл.
ΔSраз = ΔSпоз – ΔSкол – ΔSэл.
ΔSраз = ΔSпоз + ΔSкол – ΔSэл.
С точки зрения закона баланса энтропии процессы защиты окружающей среды являются:
энергетически выгодными.
энергетически не выгодными.
от энергии не зависят.
вопрос поставлен некорректно.
в зависимости от условий проведения процесса.
Какие основные уравнения лежат в основе расчетов процессов и аппаратов химической технологии:
закон сохранения массы.
закон сохранения энергии.
ни один из этих вопросов.
вопрос поставлен некорректно.
закон сохранения массы и закон сохранения энергии.
Какие системы называются двухфазными?
системы, состоящие только из твердых частиц и жидкости.
системы, состоящие только из твердых частиц и газа.
системы, состоящие только из твердых частиц.
системы, состоящие только из газа или жидкости.
системы, состоящие из твердых частиц и жидкости, а также системы, состоящие из твердых частиц и газа.
Поведение двухфазных систем определяется в основном:
концентрацией твердой фазы.
размером частиц.
концентрацией жидкой фазы.
концентрацией твердой фазы и размером частиц.
гранулометрическим составом частиц.
Двухфазная система приближается к однофазной, когда:
чем больше размер частиц и меньше их концентрация.
чем больше размер частиц и больше их концентрация.
чем меньше размер частиц и больше их концентрация.
чем меньше размер частиц и меньше их концентрация.
чем больше размер частиц и меньше их концентрация.
Как обезвоживают грубые суспензии с размером частиц более 10 мм?
грохочением.
гидроциклонированием.
при помощи вибрации.
центрифугированием.
дренажем под действием собственного веса.
Как обезвоживают суспензии с размером частиц от -10 до 2 мм?
грохочением.
гидроциклонированием.
при помощи вибрации.
сушкой.
дренажем с учетом силы тяжести.
Как обезвоживают суспензии с размером частиц от -2 до 0,5 мм?
дренажем под действием собственного веса.
дренажем под действием собственного веса и грохочением.
сушкой.
гидроциклонирование.
прокаливанием.
Как обезвоживают суспензии с размером частиц менее 0,5 мм?
дренажем под действием собственного веса.
дренажем под действием собственного веса и грохочением.
отстаиванием.
отстаиванием совместно с гидроциклонированием.
отстаиванием совместно гидроциклонированием и применением флокулянтов.
Как обезвоживают суспензии с размером частиц от -0,5 до 0,1 мм
дренажем под действием собственного веса.
дренажем под действием собственного веса и грохочением.
отстаиванием.
отстаиванием с применением флокулянтов.
отстаиванием с применением флокулянтов и гидроциклонированием.
Механические методы обезвоживания можно описать с помощью процессов:
оседания частиц в жидкости с переменной вязкостью.
фильтрации частиц через поры.
фильтрации частиц несжимаемый во времени осадок.
оседания частиц в жидкости с переменной вязкостью и фильтрации воды через поры.
фильтрации частиц через сжимаемый во времени осадок.
Можно ли достичь 100% обезвоживания с применением лишь только одного способа?
нет.
да.
в зависимости от условий.
вопрос некорректен.
это зависит от крупности материала.
Химически связанную воду называют:
кристаллизационной.
адсорбционной.
конституционной.
капиллярной.
гравитационной.
Координационно-химически связанную воду в кристалло-гидратах называют:
кристаллизационной.
адсорбционной.
конституционной.
капиллярной.
гравитационной.
Влагу на поверхности твердых тел называют:
кристаллизационной.
адсорбционной.
конституционной.
пленочной.
гравитационной.
Вода имеет конечную скорость вытекания из капилляра, эта скорость:
увеличивается по мере уменьшения гидростатического напора.
уменьшается по мере уменьшения гидростатического напора.
не зависит от гидростатического напора.
является функцией гидростатического напора.
вопрос поставлен некорректно.
Вода, остающаяся в осадке, называется:
кристаллизационной.
адсорбционной.
капиллярной
гравитационной.
обусловлена всеми механизмами образования.
Энергия связи конституционной воды равна:
тепловому эффекту реакции разложения гидрооксида металла до его окисла (100-200 ккал/моль).
тепловому эффекту удаления кристаллизационной воды 10 ккал/моль.
дифференциальной теплоте адсорбции (2-3)L, где L – скрытая теплота конденсации.
энергии удаления капиллярно удерживаемой влаги.
вопрос поставлен некорректно.
Тепловой эффект реакции при удалении кристаллизационной воды равен:
энергии связи конституционной воды.
дифференциальной теплоте адсорбции.
энергии удаления капиллярно удерживаемой влаги.
10ккал/моль.
тепловому эффекту разложения гидрооксида металла.
Дифференциальная теплота адсорбции паров зависит:
от степени заполнения поверхности.
от давления пара.
от температуры пара.
от состава пара.
от давления, температуры и состава пара.
Энергию удаления капиллярно-удерживаемой влаги можно оценить:
по тепловому эффекту удаления кристаллизационной воды.
по тепловому эффекту реакции разложения гидрооксида металла, до его окисла.
по дифференциальной теплоте адсорбции.
по величине работы перемещения объема жидкости с высоты, соответствующей капиллярному поднятию до уровня жидкости в широком сосуде.
по необходимому перепаду давлений (работа против сил вязкости).
Энергию удаления гравитационной влаги можно оценить:
по тепловому эффекту удаления кристаллизационной воды.
по тепловому эффекту реакции разложения гидрооксида металла до его окисла.
по дифференциальной теплоте адсорбции.
по величине работы перемещения объема жидкости с высоты соответствующему капиллярному поднятию до уровня жидкости в широком сосуде.
по необходимому перепаду давлений (работа против сил вязкости).
Для определения энергии связи воды с поверхностью твердого тела необходимо знать:
величины поверхностей твердых частиц.
размер пор.
диаметр капилляр в осадке.
только а и б или б и в.
а, б, в.
Макропористые материалы – материалы, размер пор которых:
менее 2*10-4 мм.
6*10-6 < δ < 2*10-4.
более 2*10-4.
менее 6*10-6 мм.
вопрос поставлен некорректно.
Материалы, относящиеся к переходному классу, имеют размер пор:
менее 2*10-4 мм.
6*10-6 < δ < 2*10-4.
более 2*10-4.
менее 6*10-6 мм.
вопрос поставлен некорректно.
Микропористые материалы - это материалы, размер пор которых:
менее 2*10-4 мм.
6*10-6 < δ < 2*10-4.
более 2*10-4.
менее 6*10-6 мм.
более 6*10-6.
Степень пористости материалов определяет величину:
внешней поверхности частицы.
величину пустого объема.
величину внутренней поверхности.
величину внутренней поверхности и пустого объема.
величину реального объема частицы.
Гигроскопичными называются тела, которые удерживают значительное количество влаги. Это происходит потому, что:
размеры пор приближаются к размерам адсорбируемых молекул воды.
адсорбция в микропорах приводит к заполнению их объема.
совместно а и б.
данные явления не зависят от указанных факторов.
данное явление обусловлено другими причинами.
Явление капиллярной конденсации отсутствует:
в больших порах δ > 2*10-4 мм.
в порах переходного размера 6*10-6 < δ < 2*10-4мм.
в малых порах δ < 6*10-6 мм.
в больших порах δ > 2*10-4 мм и малых порах δ < 6*10-6 мм.
в указанных ответах нет правильного.
Дренированием называют операцию обезвоживания:
за счет стекания жидкости по капиллярам осадка под влиянием собственного веса.
за счет стекания жидкости по капиллярам осадка под влиянием собственного веса и силы вибрации.
за счет стекания жидкости по капиллярам осадка под влиянием собственного веса и центробежной силы.
за счет стекания жидкости по капиллярам осадка под влиянием силы вибрации или центробежной силы.
за счет стекания жидкости по капиллярам осадка под влиянием силы Кориолиса.
При плотной упаковке шарообразных зерен эффективный радиус межзеренных каналов:
Rэфф = 0,51 rзер.
Rэфф = 0,41 rзер.
Rэфф = 0,47 rзер.
Rэфф = 0,31 rзер.
Rэфф = 0,21 rзер.
При дренировании чаще всего наблюдается:
турбулентный режим течения жидкости.
ламинарный режим течения жидкости.
переходный режим течения жидкости.
в начале дренирования переходной режим, а в конце - ламинарный.
в начале дренирования турбулентный режим течения жидкости, а в конце - переходный режим.
Зависит ли скорость течения жидкости от формы частиц и природы материала?
не зависит.
сильно зависит.
сильно зависит от формы частиц материала.
сильно зависит от природы материала.
сильно зависит от формы частиц материала и незначительно от природы материала.
Отстаивание - это процесс обезвоживания материала, происходящий при расслоении суспензии
под влиянием силы Кориолиса.
под влиянием силы вибрации.
под влиянием центробежной силы.
под влиянием собственного веса.
сила, под действием которой происходит расслоение суспензии, не указана.
Процесс отстаивания описывается законом Стоксом, если:
Cтв>0,1 - 1%, rтв = 100мкм - 1мм, μ - возрастающая величина, а V - скорость движения относительно твердого, соответствует значению скорости для турбулентного режима.
Cтв>0,1 - 1%, rтв = 10 > 1 мм, μ = Const, V не превышает значения для ламинарного потока.
Cтв>0,1 - 1%, rтв = 10 ÷ 100 мкм, μ - возрастающая величина, V не превышает значения для ламинарного потока.
Cтв>0,1 - 1%, rтв =10 ÷ 100 мкм, μ = Const, V не превышает значения для ламинарного течения.
среди ответов нет правильного.
При осаждении вязкость суспензии:
не изменяется.
изменяется незначительно.
изменятся, т.к. зависит от концентрации твердого тела.
изменятся, т.к. зависит от радиуса твердых частиц.
вопрос некорректен.
Правильный ответ:50.3
Жидкости, в которых величина вязкости постоянна и не зависит от скорости ее течения, называются:
неньютоновскими.
абсорбционными.
ньютоновскими.
гравитационными.
адсорбционными.
К какому классу относится концентрированная суспензия (массовое осаждение 15-25% твердого)
I.
II.
III.
IV.
суспензии не подразделяются на классы.
Суспензии какого класса подвергаются сгущению:
I и II.
I и III.
II и III.
III и IV.
II и IV.
В процессе сгущения пульпы образуется осветленная зона, которая находится:
выше границы осаждения.
ниже границы осаждения.
четкой границы осаждения не существует.
в процессе сгущения пульпы осветленный слой не образуется.
вопрос некорректен.
По кривой процесса сгущения можно определить:
степень содержания взвешенных частиц в растворе.
радиус осаждающихся частиц.
объем сосуда.
скорость осаждения твердых веществ.
состав осадка.
Удельная поверхность согласно методу Коу и Клевенжера рассчитывается как:
f = RнRж/ρжK1.
f = RнRж/ρжv0K1.
f = - RнRж/ρжv0K1.
f = RнRж v0/ρжK1.
f = RнRж v0/ρж.
Удельная поверхность согласно методу Кинча рассчитывается как:
f = 695*tp/C0H0.
f = 685*tp/C0H0.
f = 695*tp/H0.
f = tp/C0H0.
f = 65*tp/C0H0.
Какая величина определяется по формуле tc*(1/ρтв + (1/ρж)*Rcp)/f:
высота осветленной зоны.
высота переходной зоны.
высота уплотненной зоны.
высота зоны свободного падения.
из перечисленных ответов нет верного.
Скорость осаждающейся частицы под действием центробежной силы:
не достигает предельного значения.
достигает предельного значения.
остается постоянной.
в данном процессе скорость частицы определить невозможно.
вопрос некорректен.
В процессе осаждения под действием центробежной силы при Re < 0.2, когда имеет место ламинарный закон движения частиц, сила сопротивления определяется законом Ньютона:
F = 6 π μ r v.
F = 8 π μ r v.
F = 6 π μ r ρ.
F = 6 μ r v.
F = (6 π μ r v)/f.
При увеличение значения Re происходит:
увеличение роста эффективности действия центрифуг.
эффективность центрифуг не зависит от данного параметра.
уменьшение роста эффективности действия центрифуг.
увеличение значения расхода.
вопрос задан некорректно.
Фильтрование - это процесс:
обезвоживания растворов.
отделения растворимых твердых частиц с пористых перегородок.
отделения нерастворимых твердых частиц с пористых перегородок.
осаждения твердых частиц на пористые перегородки.
осаждение суспензий, содержащих большое количество мелких частиц.
По характеру процесса фильтрование бывает с образованием осадка и без него, целью этих процессов является получение товарного продукта в виде:
осадка и фильтрата соответственно.
фильтрата и осадка соответственно.
таких видов фильтрования не существует.
концентрата в обоих случаях.
вопрос некорректен.
К числу практически несжимаемых можно отнести:
гидроокиси металлов.
осадки, состоящие из легкодеформируемых материалов.
осадки, состоящие из относительно мелких кристаллических частиц менее 45 мкм.
осадки, состоящие из относительно крупных кристаллических частиц более 45 ÷ 100 мкм.
осадки, состоящие из относительно крупных кристаллических частиц более 70 ÷ 100 мкм.
Чему препятствуют вспомогательные вещества, используемые при фильтровании:
увеличению скорости фильтрования.
проникновению твердых веществ в поры фильтровальной перегородки.
увеличению эффективности фильтрования.
упрощению извлечения шлама.
вспомогательные вещества при фильтровании не используются.
В общем виде скорость течения жидкости через пористый слой определяется:
размерами пор.
перепадом давления.
а и б.
производительностью.
б и г.
Коэффициент сопротивления определяется формулой:
λ = 133/Re - 2.34.
λ = 133*Re + 2.34.
λ = Re/133 + 2.34.
λ = 133/Re + 0.34.
λ = 133/Re + 2.34.
Ламинарный режим практически существует при Re:
>50.
< 50.
= 50.
режим течения жидкости не зависит от данного параметра.
среди ответ нет правильного.
Пористость находят по формуле:
ε = (V-V0)/V.
ε = (V-V0)*V.
ε = (V-V0)/V0.
ε = (V-V0)*V0.
вопрос некорректен.
Переменная скорость фильтрования в дифференциальной форме выражается:
W = dV*Sdτ.
W = dVS/dτ.
W = dV + Sdτ.
W = dV/dτ.
W = dV/Sdτ.
Удельное и полное сопротивления связаны между собой уравнением:
Rос = r0H = - r0x0(V/S).
Rос = r0H = r0x0(V/S).
Rос = r0H + r0x0(V/S).
Rос = r0H = r0x0(V*S).
Rос = r0H = r0(V/S).
Как гидравлическое сопротивление осадка Roc может меняться по ходу процесса из-за:
гидравлическое сопротивление остается на протяжении всего процесса постоянным.
возрастает из-за засорения пор мелкими частицами.
возрастает из-за некоторой сжимаемости осадка.
уменьшается из-за применения вспомогательных веществ.
б и в.
В каких случаях можно проинтегрировать дифференциальное уравнение фильтрации при допущении постоянства удельного сопротивления осадка?
при ΔР = Const.
при dV/dτ = const.
при ΔР и dV/dτ = const.
в случаях а, б и в.
в случаях а и в.
Если жидкость фильтруется сквозь осадок постоянной толщины, то:
ΔР=0, W=const.
ΔР=const, W=const.
ΔР=0, W=0.
ΔР=1, W=0.
ΔР=0, W=∞.
Полный цикл работы фильтра периодического действия состоит из операций:
загрузки суспензии, фильтрования, промывки осадка, продувки его и удаления.
подготовки фильтра, загрузки суспензии, фильтрования, промывки осадка и его продувки.
подготовки фильтра, загрузки суспензии, фильтрования, промывки осадка, продувки его и удаления.
подготовки фильтра, загрузки вспомогательных веществ, фильтрования, промывки осадка, продувки его и удаления его.
подготовки фильтра, промывки суспензии, загрузки суспензии, фильтрования, продувки его и удаления.
После прохождения условной скорости фильтрации максимума, условная скорость:
резко уменьшается.
уменьшается медленно.
увеличивается постепенно.
увеличивается резко.
не изменятся.
Какими свойствами должна обладать фильтровальная перегородка?
способностью хорошо задерживать твердые частицы суспензии и небольшим гидравлическим сопротивлением.
возможностью легкого отделения осадка и достаточной механической стойкостью.
стойкостью к воздействию среды, реагентов, температуры, а также высокой пористостью.
а, б, и стойкостью к воздействию среды, реагентов, температуры.
среди ответов нет правильного.
От размера частиц суспензии, свойств осадка, его удельного сопротивлении, свойств осадка сниматься, производительности зависит:
выбор фильтра.
выбор циклона.
выбор вспомогательных веществ.
размер фильтровальной перегородки.
среди ответов нет правильного.
Удельная производительность вычисляется по формуле:
qw = (St)/Q.
qw = - Q/(St).
qw = Q/(St).
qw = -St/Q.
qw = (Qt)/S.
По формуле Sфq рассчитывается:
производительность фильтра.
скорость фильтра.
скорость частиц суспензии.
высота осадка.
пористость.
Скорость фильтрации меняется от времени в зависимости от:
давления и температуры воздуха.
вида суспензии.
от вида взвешенных частиц.
степени изношенности и забивки фильтровальной перегородки.
от количества взвешенных частиц.
При процессе центробежного фильтрования среднеарифметическое значение площади осадка вычисляется по формуле:
Sср.лог. = (r2 – r1)h.
Sср.лог. = (r2 – r1)πH.
Sср.лог. = (r2 + r1)πh.
Sср.лог. = (r2 – r1)πh.
Sср.лог. = (r2 – r1)/πh.
Осаждение суспензий, содержащих большое количество мелких частиц, ускоряет процесс:
фильтрации.
осаждения.
агрегирования.
абсорбции.
адсорбции.
Закон Эйнштейна-Смолуховского определяется формулой:
ΔХ = |
|
|
 Скачать 7.02 Mb.
Скачать 7.02 Mb.