ТОЗОС часть2. Учебнометодические разработки для самостоятельной работы студентов по курсу
 Скачать 7.02 Mb. Скачать 7.02 Mb.
|
|
4.2.7. Дифференциальные функции распределения по крупности Дифференциальные функции распределения по крупности показывают число зерен или массовый выход каждого класса крупности в данном материале. Материал, состоящий из смеси зерен разных размеров, разделенный на классы крупности, можно рассматривать как статистический коллектив. Размер зерен будет аргументом коллектива, а общее число зерен в пробе материала или ее общая масса составят числовой или массовый объем статистического коллектива. Число зерен в каждом классе, или их массу, называют численностью класса, частотой или абсолютной частостью, а частоты классов, отнесенные к объему коллектива, - относительными частостями классов. Если в прямоугольных координатах по оси абсцисс отложить крупность классов и на соответствующих интервалах крупности построить прямоугольники, площади которых будут пропорциональны частоте класса, то получим гистограмму распределения зерен материала. Это равнозначно построению прямоугольников высотой, равной частости на единицу длины интервала, на интервале как основании прямоугольника. При уменьшающемся интервале ступенчатая линия, сверху ограничивающая прямоугольники, приближается к плавной кривой; в пределе она дает дифференциальную функцию распределения (рис. 4.14, е). Ординаты функции распределения γ(х)выражают частость на единицу длины бесконечно узкого интервала по оси абсцисс, а площадь под кривой определяет число объектов (число зерен, массовый выход их) в соответствующих промежутках. Зерна, диаметры которых меньше хпи больше хп1, образуют n-й класс - xn + хп-1 с интервалом крупности Δхп= хп хп1. Если число зерен в этом классе Nn, а масса их Wn, то относительная частость по числу зерен будет Nn/ nи по массе Wn/ W, где N - общее число зерен в пробе материала, a W - их общая масса. Таким образом, для построения функции распределения по числу зерен следует по оси абсцисс на интервале хп хп-1построить прямоугольник высотой Nn/ NΔхп, а затем - прямоугольники для всех других классов и соединить кривой точки на серединах верхних сторон прямоугольников. Относительное число зерен в бесконечно малом интервале dх и в классе хп хп-1 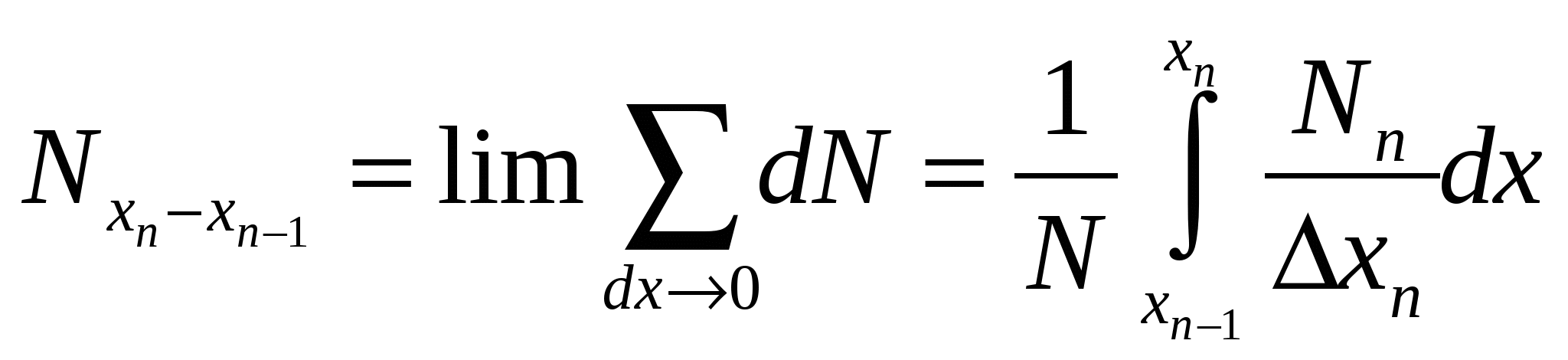 . .Аналогично имеем следующее выражение для массовых выходов зерен класса хn— хп1; 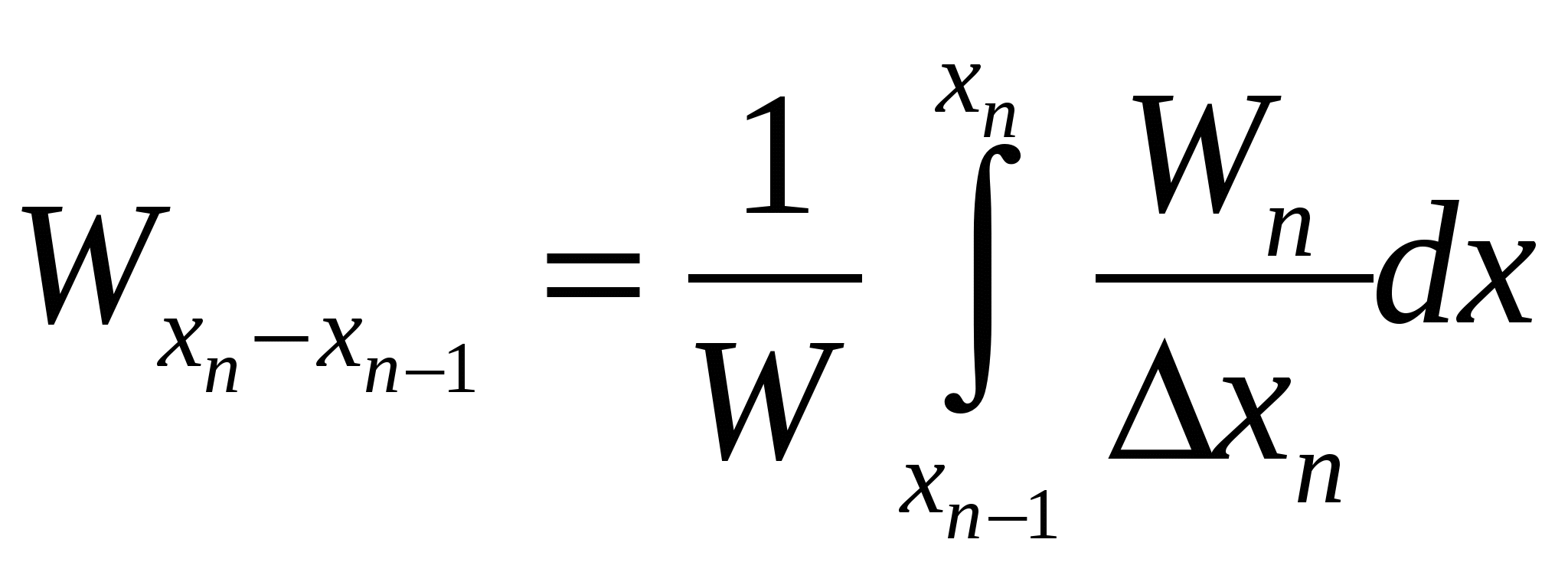 . .Последнее выражение соответствует уравнению (4.19): В этом уравнении пределы интегрирования определяют границы класса крупности, массовый выход которого определяется, а подынтегральная функция f(x) есть дифференциальное распределение по крупности. Кривые распределения дают более наглядное представление о гранулометрическом составе сыпучих материалов в сравнении с суммарными характеристиками крупности. В классах с наибольшим выходом кривая показывает максимум, а при отсутствии в материале зерен какого-либо размера падает до нуля. Выход класса на кривой распределения пропорционален площадям, ограниченным кривой и двумя ординатами, проведенными на диаметрах, ограничивающих данный класс. Дифференциальные функции распределения и суммарные характеристики крупности полностью характеризуют гранулометрический состав материала с точки зрения математической статистики. Возможен аналитический переход от одной кривой к другой, если известно уравнение какой-либо из них (см. формулу 4.19). 4.2.8. Вычисление поверхности и числа частиц по уравнениям суммарной характеристики крупности Если известно уравнение суммарной характеристики крупности, то общий ход вычисления поверхности и числа зерен может быть принят следующий. Пусть уравнение характеристики «по минусу» будет где Тогда В 1 г материала плотностью σ (г/см3) объем элементарного класса (см3) Для одного зерна кубической формы объем равен х3, аповерхность 6х2. Число зерен в элементарном классе Число зерен и их поверхность в классе мельче х2и крупнее х1находят интегрированием из выражений в пределах от х1до х2: 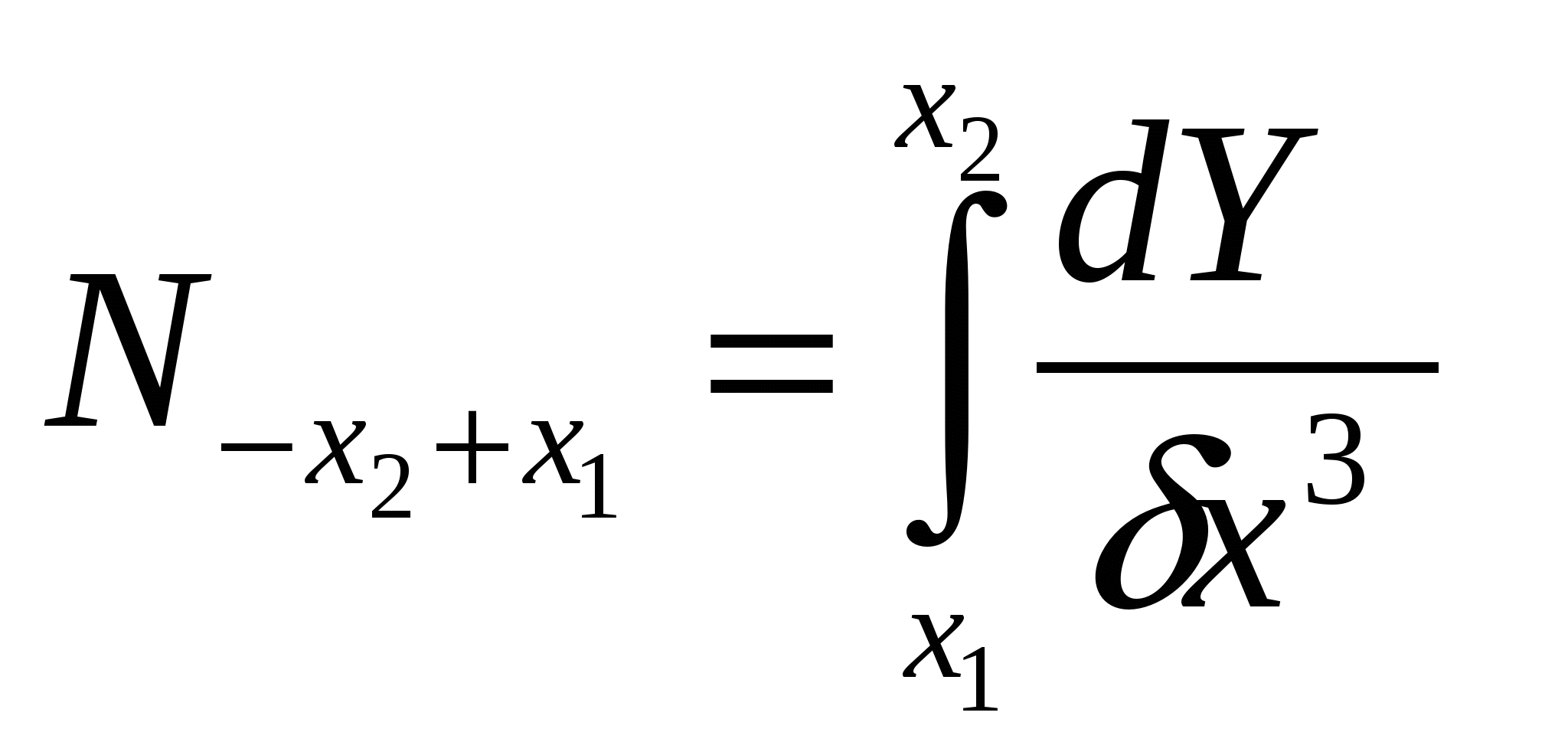 и и 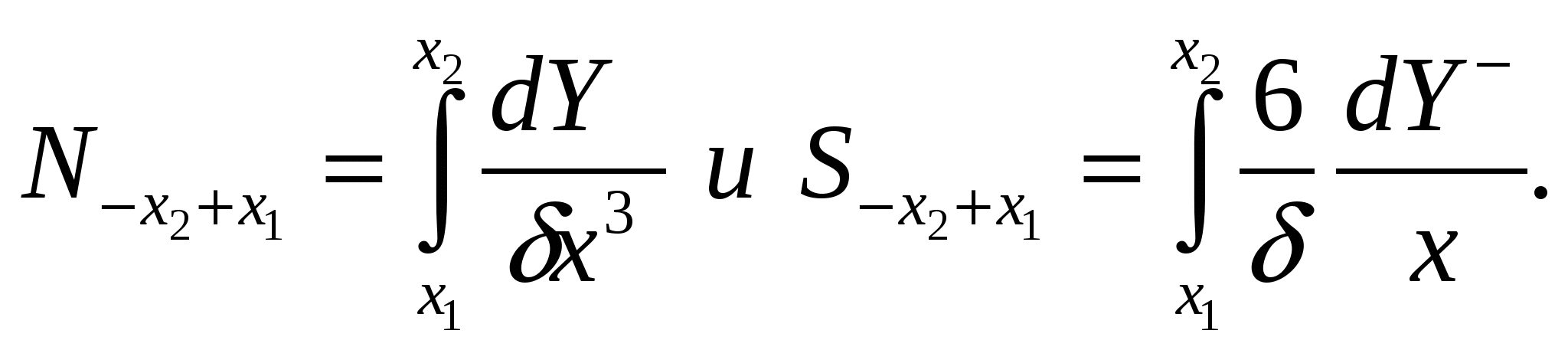 При вычислении поверхности безразлично, будет ли принят формой зерен куб или шар. В самом деле, если принять все зерна шарообразной формы, то получим 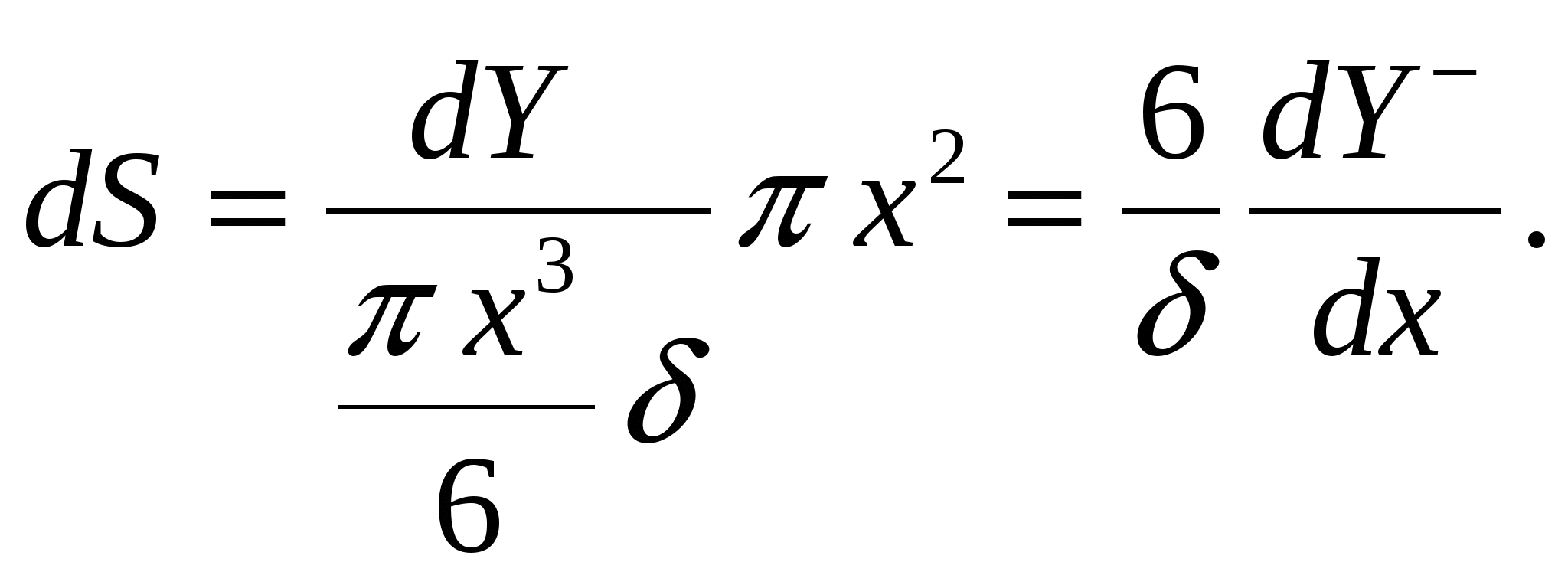 Конкретные выражения для числа и поверхности зерен в заданном классе крупности - х2+ х1 в предположении, что распределение соответствует уравнению Розина-Раммлера. 4.2.9. Эффективность процесса грохочения Для количественной оценки полноты отделения мелкого материала от крупного при грохочении введено понятие эффективности (точности) грохочения. Эффективностью грохочения называют выраженное в процентах или в долях единицы отношение массы подрешетного продукта к массе нижнего класса в исходном материале. Нижним классом называют материал, крупность которого меньше размера отверстия сита грохота. Содержание нижнего класса в любом продукте можно определить тщательным рассевом пробы на сите с отверстиями размерами, равными размерам отверстий сита грохота. Эффективность грохочения можно также определить как извлечение нижнего класса в подрешетный продукт. Рассмотрим баланс материала при грохочении (рис. 4.15): Также имеем: 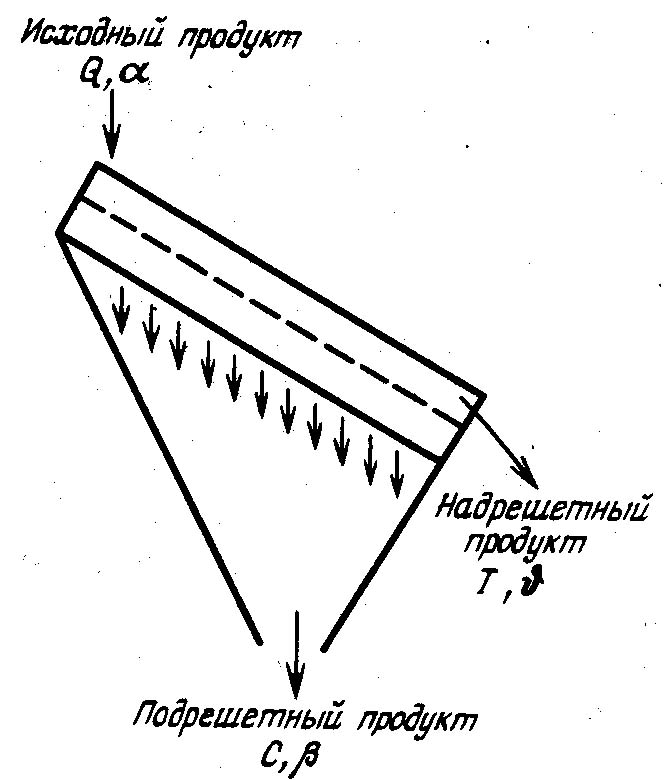 Рис. 4.15. Определение эффективности грохочения Эффективность грохочения (%), согласно определению, Для определения эффективности грохочения по формуле (4.27) необходимо знать массу исходного материала Q и подрешетного продукта С, непосредственное определение которых при непрерывном процессе на производств представляет известные трудности. Поэтому отношение масс C/Q(выход подрешетного продукта) определяют по содержанию нижнего класса в исходном материале и надрешетном продукте. Баланс нижнего класса Заменив Т, воспользовавшись формулой (4.26), получим откуда Подставив отношение C/Qв формулу (4.27), получим в окончательном виде формулу для определения эффективности грохочения (%) по нижнему классу Содержание нижнего класса и определяют тщательным рассевом проб исходного материала и надрешетного продукта на ситах с отверстиями той же величины и формы, что и в сите грохота, эффективность грохочения которого определяют. Подобным же образом можно определить эффективность грохочения по любому суммарному или узкому классу крупности, который мельче размера отверстий сита грохота, считая эффективностью грохочения по данному классу отношение массы этого класса в подрешетном продукте к массе того же класса в исходном материале. К ранее принятым обозначениям добавим Эффективность (%) по любому заданному классу крупности Выход (%) подрешетного продукта C/Qнаходят из баланса данного класса при грохочении: Формула (4.29) для эффективности по нижнему классу получится из формулы (4.30), если подставить в нее значение В некоторых случаях результаты грохочения оценивают упрощенно по содержанию Пример. Дано: содержание нижнего класса в надрешетном продукте - 10%, выход подрешетного продукта - 40%. Определить эффективность грохочения. Выход надрешетного продукта составит 100 40 = 60 %. На 60 массовых единиц надрешетного продукта приходится 60*10/100 = 6 единиц нижнего класса. Общая доля нижнего класса в надрешетном и подрешетном продуктах, т. е. в материале, поступающем на грохот, составит 6 + 40 = 46 массовых ед. Эффективность грохочения E=(40/46)100=87% 4.2.10. «Легкие», «трудные» и «затрудняющие» частицы Просеивание зерен нижнего класса сыпучего материала сквозь сито можно рассматривать как операцию, состоящую из двух стадий: зерна нижнего класса должны пройти сквозь слой зерен верхнего класса, чтобы достигнуть поверхности сита; зерна нижнего класса должны пройти через отверстия сита. Осуществлению обеих стадий помогает соответствующий характер движения короба грохота, приводящий слой зерен на сите в разрыхленное состояние и освобождающий сито от зерен, застрявших в его отверстиях. При встряхивании короба в слое зерен, лежащем на сите, происходит их сегрегация (расслоение по крупности), причем наиболее крупные зерна оказываются в верхнем слое, а наиболее мелкие - на поверхности сита. Последние легко достигают поверхности сита и проходят через его отверстия. Но зерна, близкие по величине к размеру отверстий сита, с трудом проходят в промежутках между более крупными зернами слоя материала, лежащего на сите, а также и через отверстия сита. Практика грохочения показала, что зерна, диаметр которых меньше чем три четверти отверстия сита, легко проходят в промежутках между крупными зернами материала на сите и по достижении ими поверхности сита немедленно проваливаются через отверстия. Такие зерна в отношении их проходимости называют «легкими». Зерна крупнее трех четвертей отверстия сита с трудом проходят в промежутках между крупными зернами и через отверстия сита. Эта трудность прохождения прогрессивно возрастает по мере приближения диаметра зерен к размеру отверстий сита. Такие зерна называют «трудными». Зерна, диаметр которых более полуторного размера отверстия сита, существенно не влияют на перемещение «легких» и «трудных» зерен к поверхности сита. На сите нижний слой материала, состоящий из зерен диаметром меньше полуторного размера отверстия сита, затрудняет проникновение к его поверхности близких к ним по крупности «трудных» зерен. Кроме того, зерна, близкие по диаметру к размеру отверстия сита, но больше их, легко застревают в отверстиях и забивают сито. Зерна, размер которых больше отверстий сита, но меньше полуторной величины их, называют «затрудняющими». Чем меньше в исходном материале «трудных» и «затрудняющих» зерен, тем легче его грохочение и тем выше, при прочих равных условиях, эффективность грохочения. Характеристики крупности легко- и трудногрохотимого материала на ситах с размером отверстий l показаны на рис. 4.16. 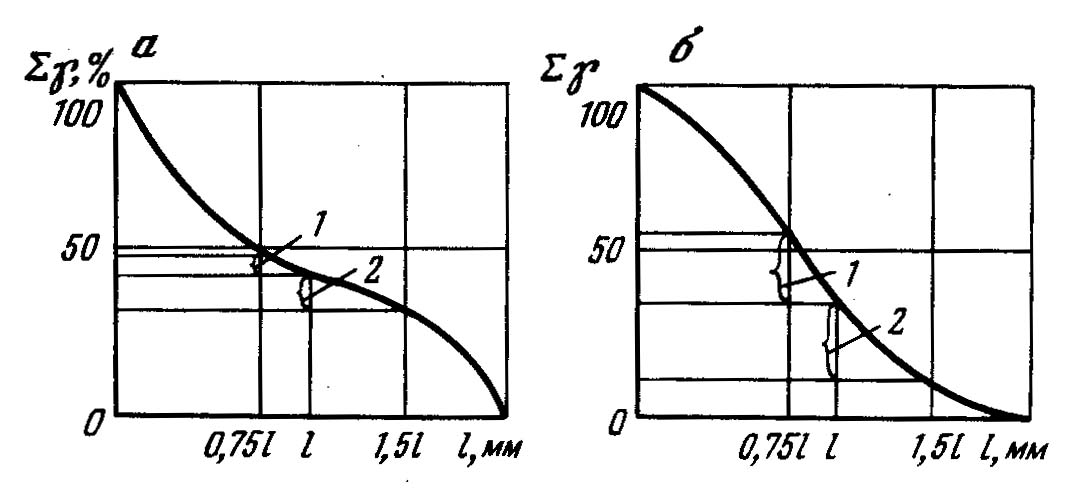 Рис. 4.16. Суммарные характеристики крупности: а - легкогрохотимого материала; б - трудногрохотимого материала: 1 - выход «трудных» зерен; 2 - выход «затрудняющих» зерен Эффективность грохочения по «трудным» зернам определяют по общей формуле (4.30), в которой 4.2.11. Вероятность прохождения частиц через отверстия сита Рассмотрим условия прохождения отдельного зерна через отверстия сита. Вероятность Р какого-либо события равна отношению числа случаев т, благоприятствующих наступлению данного события, к числу всех возможных случаев п, при которых данное событие может произойти. Причем все случаи должны быть равновозможными и несовместимыми. Следовательно, вероятность Р = т / п. При т = 0 вероятность Р = 0, т. е. ни один случай не благоприятствует наступлению события (невозможность), при т = п вероятность P=1, т.е. каждый случай благоприятствует событию (достоверность). Величина N, обратная вероятности Р, определяет вероятное число случаев, при котором данное событие может иметь место: N = 1 / Р. Предположим, что мы имеем сито из бесконечно тонкой проволоки с квадратными отверстиями размером l. Допустим также, что шарообразные зерна диаметром dпри грохочении падают перпендикулярно к плоскости сита. Будем считать, что зерна проходят через отверстия беспрепятственно, если они не касаются проволоки, т. е. когда центр зерна при падении проектируется на заштрихованную площадь (l d)2на рис. 4.17, а. Можно считать, что число случаев, благоприятствующих прохождению зерна через отверстие, пропорционально заштрихованной площади (l d)2, а число всех возможных случаев падения зерна на отверстие пропорционально его площади l2. Вероятность прохождения зерна через отверстие определится отношением площадей: Тогда величина N, обратная вероятности Р, определит вероятное число отверстий, которое необходимо встретить зерну, чтобы в одно из них пройти сквозь сито. 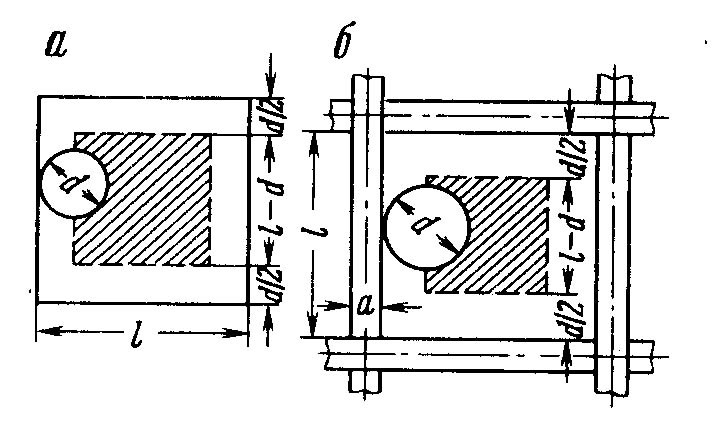 Рис. 4.17. Схема прохождения зерна сквозь отверстие сита Значения Р и N для различных отношений d / lприведены в табл. 4.15, по данным которой построен график (рис. 4.18). Из графика видно, что увеличение диаметра зерна более 0,75l вызывает значительное возрастание числа отверстий для прохождения зерна сквозь сито. Таблица 4.15 Вероятность прохождения зерна через отверстие в зависимости от его относительного размера
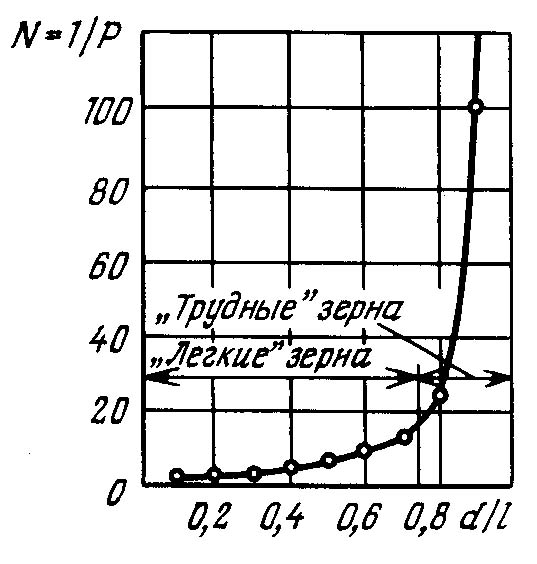 Рис. 4.18. Зависимость обратной вероятности прохождения зерен через сито 1/р от относительного размера зерна d/l Следовательно, теория вероятностей подтверждает принятое практикой деление зерен на «легкие» (d< 0,75l) и «трудные» (d> 0,75l). Если учитывать толщину проволок сита (см. рис. 4.17, б), то, рассуждая аналогично предыдущему, получаем следующее выражение для вероятности прохождения зерна сквозь сито: Первый член этого выражения l2/(l+а)2 - коэффициент живого сечения сита. Отсюда видно, что вероятность прохождения зерна прямо пропорциональна живому сечению сита. Если учесть что частица может пройти сквозь отверстие после отражения от проволоки, то вероятность: 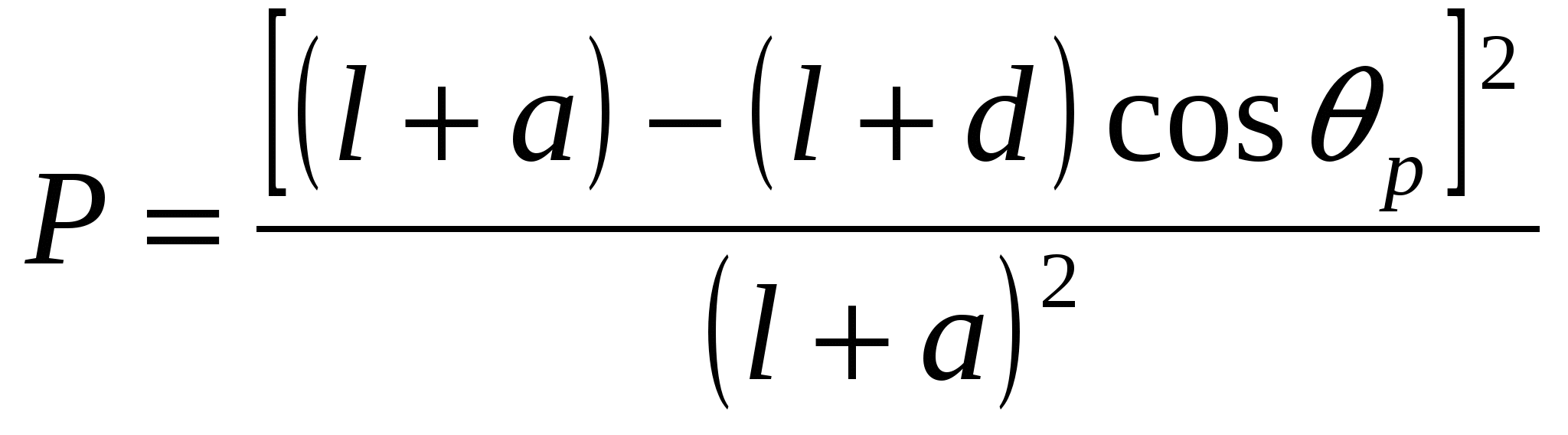 , (4.32) , (4.32)где |
