Статистика задачи. Статистика Решебник. Учебнометодическое пособие по дисциплине Статистика составлено по разделу Теория статистики
 Скачать 359.42 Kb. Скачать 359.42 Kb.
|
22 % P 38 %p W W 0,3 0,08 или Задача № 2. Используя данные и решение задачи № 1 определите, какое число пачек чая следует подвергнуть наблюдению при условии, что предельная ошибка выборки для бесповторного отбора при определении среднего веса пачки чая была бы не более 0,1 грамма при вероятности 0,997, а предельная ошибка доли пачек чая с весом 51-55 грамм была бы не более 3 %. Решение: Для определения численности выборочной совокупности при механическом бесповторном отборе используются формулы: Для средней: t2 2 N nx 32 3,04 400 10944 349 пачек x x 2 N t2 2 0,12 400 32 3,04 31,36 Для доли: t2 w 1 w N 32 0,3 1 0,3 400 756 n 2 w N t2w 1 w 0,032 400 32 1 0,3 2,25 336 пачек ТЕМА 6. СТАТИСТИЧЕСКИЕ МЕТОДЫ ИЗУЧЕНИЯ СВЯЗЕЙ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ руб. Задача № 49. Имеются следующие данные по торговым предприятиям фирм, тыс.
Для установления связи между издержками обращения и товарооборотом рассчитайте ранговый коэффициент Спирмена. Задача № 50. По ряду районов края определены: среднесуточное количество йода в воде и пище и пораженности населения заболеванием щитовидной железы.
Для оценки тесноты связи пораженности заболеванием щитовидной железы с количеством йода в воде и пище определите коэффициенты корреляции рангов Спирмена, Кендалла и Фехнера. Задача № 51. При проверке качества товара, поступившего в магазин, получены следующие данные, в %%:
Установите тесноту связи между качеством товара и удельным весом стандартной и нестандартной продукции с помощью коэффициентов взаимной сопряженности Пирсона и Чупрова. Задача № 52. Используя коэффициент взаимной сопряженности Пирсона ответьте на вопрос: являются ли конфликтные ситуации фактором гипертонической болезни?
Задача № 53. С помощью коэффициента взаимной сопряженности Пирсона определите: является ли работа на компьютере фактором ухудшения зрения, чел.
Задача № 54. По материалам одного из обследований домашних хозяйств получены следующие данные:
Найдите коэффициент ассоциации между источниками доходов (наличием дохода от предпринимательской деятельности) и уровнем дохода. Задача № 55. В результате обследования населения региона получены следующие данные:
Установите тесноту связи между семейным положением и наличием садового участка, рассчитав коэффициент контингенции. Задача № 56. Зависимость между объемом реализации и валовой прибылью по предприятиям одной из отраслей характеризуется следующими данными:
Для изучения влияния объема реализации на величину валовой прибыли постройте уравнение прямой, рассчитайте параметры уравнения и определите тесноту связи с помощью линейного коэффициента корреляции. Сделайте выводы. Задача № 57. По 16 предприятиям, изготавливающим одноименные запасные детали к сельскохозяйственным машинам, были получены следующие данные об объеме производства деталей и долей ручных работ:
Определите вид корреляционной зависимости, постройте уравнение регрессии, рассчитайте параметры уравнения, коэффициент эластичности между фактором и результатом, вычислите показатель тесноты связи, проанализируйте полученные данные. Решение типовых задач Задача№ 1. Экспертами оценивались вкусовые качества вин. Суммарные оценки получены следующие:
Согласуетсялиоценка вина с его ценой? Проверимэту гипотезу методом ранговой корреляции Спирмена и коэффициентом Фехнера. Решение: Оценку тесноты связи с помощью коэффициента Спирмена и Фехнера рассчитываем в табличной форме:
Коэффициент Спирмена: 6d2 6 27 162 Р 1 n(n2 1) 1 10(100 1) 1 990 1 0,164 0,836 Следовательно, связь прямая и тесная. Проверяем значимость полученных результатов по t-критерию t P 0,836 4,309 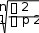 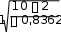 Стьюдента p . При уровне Стьюдента p . При уровнезначимости 0,05 tT 2,262 . Следовательно, значимость результатов подтверждается т.к. tp tT. Для определения коэффициента Фехнера рассчитаем среднее значение цены: x x 1,57 1,602,002,10 1,70 1,85 1,80 1,152,302,10 1,817 1,82 у.е. n 10 и среднее значение оценки x x и y y y y 155 15,5 балла. n 10 Тогда количество совпадений знаков отклонений будет восемь, а несовпадений два. Отсюда коэффициент Фехнера: К a b 8 2 0,6 фa b 8 2 Следовательно, связь прямая и существенная. Задача № 2. На основании следующих условных данных необходимо исследоватьсвязь между успеваемостью студентов-заочников одного из вузов и их работой по специальности с помощью коэффициентов ассоциации и контингенции.
Решение: Коэффициент ассоциации: Ка ad bcad bc 180 60 140 20 180 60 140 20 8000 13600 0,6 Связь подтверждается, так как Коэффициент контингенции: Ka 0,5 . Kk ad bc   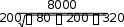 8000 800032000 0,3 Связь подтверждается, так как Kk 0,3 . Задача № 3. С помощью коэффициентов взаимной сопряженности Пирсона и Чупрова необходимо исследовать связь между себестоимостью продукции и производительностью труда на основании нижеследующих данных:
Решение: 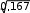 Коэффициент Пирсона: Коэффициент Пирсона: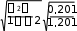 KП KП 0,4 , так как n 2 2 2 2 2 2 2 2 2 xy192 12 9 7 18 15 4 10 26 1 2 ny 30 40 50 30 40 50 30 40 50 nx 40 40 40 0,431 0,356 0,414 1,201, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
