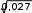Статистика задачи. Статистика Решебник. Учебнометодическое пособие по дисциплине Статистика составлено по разделу Теория статистики
 Скачать 359.42 Kb. Скачать 359.42 Kb.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | А | В |
| | Месяц | Товарооборот, млн. руб. |
| 1 | Январь | 18,9 |
| 2 | Февраль | 24,2 |
| 3 | Март | 23,7 |
| 4 | Апрель | 24,8 |
| 5 | Май | 19,5 |
| 6 | Июнь | 19,2 |
| 7 | Июль | 19,7 |
| 8 | Август | 21,5 |
| 9 | Сентябрь | 22,3 |
| 10 | Октябрь | 20,7 |
| 11 | Ноябрь | 23,5 |
| 12 | Декабрь | 20,4 |
Активизируем любую свободную ячейку, в которой мы хотим поместить результат вычисления того или иного показателя. Например, В16. Запускаем мастер функций командой Функция из меню Вставка или щелчком по кнопке вызова мастера функций на панели управления – fx. В открывшемся диалоговом окне Мастер функций – шаг 1 из 2 выбираем категорию Статистические и затем перемещаем строку выделения по списку функций до необходимой статистической функции. В нижней части окна будет представлена краткая информация о выделяемых функциях. В списке функций вы найдете все вычисленные для нашего примера функции:
СРЗНАЧ – рассчитывает среднюю арифметическую простую для заданных аргументов;
МОДА – отображает наиболее часто встречающиеся значения аргументов;
МЕДИАНА – рассчитывает медиану заданных аргументов;
СТАНДОТКЛОН – оценивает генеральное среднее квадратическое отклонение по выборке (если совокупность является генеральной, следует воспользоваться функцией СТАНДОТКЛОНП);
ДИСП – оценивает генеральную дисперсию по выборке (если совокупность является генеральной, следует воспользоваться функцией ДИСПР) и др.
Предположим, мы хотим рассчитать среднее квадратическое отклонение. После выбора функции щелкаем по кнопке ОК для перехода в следующее диалоговое окно Аргументы функции, в котором необходимо задать аргументы. Задать аргументы можно разными способами. Например, выделить блок ячеек с исходными данными, в нашем случае В4:В15. Для этого устанавливаем указатель мыши в ячейку В4 и, удерживая левую кнопку мыши, протаскиваем указатель до ячейки В15. Убедитесь, что в окне Аргументы функций появилась запись В4:В15, а в строке формул отражена функция, по которой будет производиться вычисление – = СТАНДОТКЛОНП(В4:В15). Щелкаем ОК. В ячейке В16 появляется результат вычислений, равный 2,016322.
Возможен и другой порядок расчета. После формирования на рабочем листе Excel таблицы с исходными данными в меню Сервис выбираем команду Анализ данных. Появляется окно с одноименным названием, в котором представлен список, реализованных в Excel методах статистической обработки данных. Выделяем указателем мыши режим Описательная_статистика'>Описательная статистика и щелкаем по кнопке ОК. В диалоговом окне режима Описательная статистика задаем параметры:
Выходной интервал – В4 : В15.
Группирование – по столбцу.
Выходной интервал – указываем любую свободную ячейку. Она будет верхней левой ячейкой выходной таблицы с результатами вычислений.
Итоговая статистика – устанавливаем в активное состояние. Щелкаем
ОК.
Показатели, рассчитанные в данном режиме, представлены в таблице.
Итоговая статистика:
| А | В |
| Среднее | 21,53 |
| Стандартная ошибка | 0,61 |
| Медиана | 21,10 |
| Мода | #Н/Д |
| Стандартное отклонение | 2,11 |
| Дисперсия выборки | 4,44 |
| Эксцесс | -1,55 |
| Асимметричность | 0,29 |
| Интервал | 5,90 |
| Минимум | 18,90 |
| Максимум | 24,80 |
| Сумма | 258,40 |
| Счет | 12,00 |
Обратите внимание, что показатель среднее квадратическое отклонение (стандартное отклонение) несколько отличается от рассчитанного ранее. Это связано с тем, что в режиме Описательная статистика все функции реализуются по формулам для выборочных совокупностей.
ТЕМА 5. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Задача № 44.
Для определения срока службы оборудования было проведено 10 %-е выборочное обследование по методу случайного бесповторного отбора, в результате которого получены следующие данные:
| Срок службы, лет | Количество оборудования |
| А | 1 |
| До 4 | 11 |
| 4-6 | 24 |
| 6-8 | 35 |
| 8-10 | 25 |
| 10 и более | 5 |
| Итого | 100 |
С вероятностью 0,997 определите предельную ошибку выборки и пределы, в которых ожидается средний срок службы оборудования.
С вероятностью 0,954 определите предельную ошибку репрезентативности для доли и пределы удельного веса оборудования со сроком службы более 10 лет.
Задача № 45.
Принимая распределение оборудования по сроку службы, приведенного в задаче № 44, за результаты ранее проведенного выборочного наблюдения, рассчитайте, какое количество оборудования подвергнуть наблюдению при условии, что предельная ошибка выборки при определении среднего срока службы была бы не более одного года при вероятности 0,997, а предельная ошибка доли оборудования со сроком службы 8-10 лет при вероятности 0,954 была бы не более 5 %.
Задача № 46.
Для оценки средней урожайности пшеницы посевную площадь совхоза в 5000 га разделили на 50 равных участков. Из них по методу случайной бесповторной выборки отобрали пять участков, где произвели сплошной учет фактического урожая. В результате были получены следующие данные:
| Показатели | Номер участка | ||||
| 1 | 2 | 3 | 4 | 5 | |
| А | 1 | 2 | 3 | 4 | 5 |
| Средняя урожайность, ц/га | 26 | 27 | 28 | 29 | 30 |
| Погибшие посевы, % | 3,0 | 2,5 | 2,0 | 1,5 | 1,0 |
Определите:
с вероятностью 0,997 предельную ошибку выборочной средней и границы, в которых будет находиться средняя урожайность по совхозу;
с вероятностью 0,954 предельную ошибку выборочной доли и границы, в которых будет находиться процент погибших посевов пшеницы.
Задача № 47.
С целью определения среднего эксплуатационного пробега 10000 шин легковых автомобилей, распределенных на партии по 100 штук, проводится серийная 4 %-я бесповторная выборка. Результаты испытания отобранных шин характеризуются следующими данными:
| Показатели | Партии | |||
| 1 | 2 | 3 | 4 | |
| А | 1 | 2 | 3 | 4 |
| Средний эксплуатационный пробег шин, тыс. км. | 40 | 42 | 45 | 48 |
| Доля шин с пробегом не менее 42 тыс.км. | 0,80 | 0,85 | 0,90 | 0,95 |
шин;
Определите:
среднюю ошибку репрезентативности эксплуатационного пробега
среднюю ошибку репрезентативности удельного веса шин с
пробегом не менее 42 тыс. км;
с вероятностью 0,954 пределы, в которых будет находиться средний эксплуатационный пробег всех исследуемых шин;
с вероятностью 0,954 пределы, в которых будет находиться доля шин, пробег которых не менее 42 тыс. км. в генеральной совокупности.
Задача № 48.
Используя условие и решение задачи № 47, определите вероятность того, что:
предельная ошибка выборки при установлении среднего эксплуатационного пробега шин не превышает 40 тыс. км.;
доля шин с пробегом не менее 42 тыс. км. будет находиться в пределах 83 %-92 %.
Решение типовых задач
Задача№1.
Для проверки веса чая в пачках произведена 25 %-я механическая выборка, по результатам которой получены следующие данные:
| Вес пачки чая, грамм. | Количество пачек |
| А | 1 |
| 47-49 | 20 |
| 49-51 | 50 |
| 51-53 | 20 |
| 53-55 | 10 |
| Итого | 100 |
Определите:
с вероятностью 0,954 предельную ошибку выборки и границы, в которых можно ожидать средний вес пачки чая во всей партии;
с вероятностью 0,954 предельную ошибку выборки для доли пачек чая весом 51-55 грамм.
Решение:
Для нахождения среднего веса пачки в выборочной совокупности можно использовать метод моментов, так как интервал группировки равный.
Расчетная таблица
| Вес пачки чая, грамм. | Количество пачек ( f) | Середина интервала ( x) | x AA 50 | x A i i 2 | x A fi | x A2 f i |
| А | 1 | 2 | 3 | 4 | 5 | 6 |
| 47-49 | 20 | 48 | -2 | -1 | -20 | 20 |
| 49-51 | 50 | 50 | - | - | - | - |
| 51-53 | 20 | 52 | 2 | 1 | 20 | 20 |
| 53-55 | 10 | 54 | 4 | 2 | 20 | 40 |
| Итого | 100 | Х | Х | Х | 20 | 80 |
1) Средний вес пачки чая в выборочной совокупности:
x m1 i A 0,2 2 50 50,4
так как:
гр.,
x A f
m1
i
f
20 100
0,2
При бесповторном отборе предельная ошибка выборки для среднего веса пачки чая определяется по формуле:
 x t ,
x t ,где t– коэффициент доверия, равный при вероятности 0,954 двум, n
– численность выборочной совокупности, равная 100, N – численность
генеральной совокупности, равная при 25 % отборе 100
0,25
400 .
Дисперсия среднего веса пачки чая в выборочной совокупности по методу моментов:
2
2 i2 m
m2 4 0,8 0,22 3,04 ,
1
x A2
так как
m2
f
i
f
80
100
0,8
Следовательно, границы генеральной средней будут
x 50,4гр. 0,3гр.
2) Предельная ошибка доли пачек чая с весом 51-55 гр. при бесповторном отборе определяется по формуле:
 w t ,
w t ,где w– доля пачек чая с весом 51-55 гр.
В выборочной совокупности
w 20 10 0,3
100
или 30 %
 w 2 или 8 %.
w 2 или 8 %.Тогда доля пачек с весом 51-55 грамм в генеральной совокупности