Статистика задачи. Статистика Решебник. Учебнометодическое пособие по дисциплине Статистика составлено по разделу Теория статистики

• Название: Учебнометодическое пособие по дисциплине Статистика составлено по разделу Теория статистики
• Анкор: Статистика задачи
• Дата: 04.06.2022
• Размер: 359.42 Kb.
• Имя файла: Статистика Решебник.docx
• Тип: Учебно-методическое пособие; #569460
• страница: 7 из 23

 ^129,8  1,62 (кг) 80

г) дисперсия: ^2

_(x x)² f

 <sub> f

</sub> 313,2

80
 3,915

д) среднее квадратическое отклонение: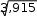
    1,98 (кг)
е) линейный коэффициент вариации:

V_d

^d100 %  ^1,62 100 %  23,5 %.

x 6,9

Задача № 2.

На основании нижеследующих данных определите: а) средний размер основных промышленно-производственных фондов на один завод (упрощенным способом); б) дисперсию (упрощенным способом); в) среднее квадратическое отклонение; г) коэффициент вариации.

Группы заводов по стоимости основных фондов, млн. руб.	Число заводов ( f)	Середина интервала ( x)	x A A 9	x A i i 2	( x A) fi	( x A)2 f i
А	1	2	3	4	5	6
4-6	2	5	-4	-2	-4	8
6-8	3	7	-2	-1	-3	3
8-10	5	9	-	-	-	-
10-12	6	11	2	1	6	6
12-14	4	13	4	2	8	16
Итого	20	Х	Х	Х	7	33

Решение:

Так как интервал группировки равный, для расчета можно использовать упрощенный метод моментов (и для средней, и для дисперсии):

x m₁  i А
а) средний размер основных фондов,
где ^m₁ момент первой степени:



_ x A_{ f}

m₁ 

 


i


_{  } 7

f 20

 0,35

, тогда

1

2

2
x 0,35  2  9  9,7

млн. руб.

б) дисперсия ^2

 i²  m

^{ m2 }, где ^m


_ x A_2

m₂ 

  ^f


i
 

_ f

_ 33

20
 1,65
, тогда

 ²  2² (1,65  0,35² )  6,11

в) среднее квадратическое отклонение

  

6,11  2,47

млн.руб.

г) коэффициент вариации:

V  ^

d _x

100 % 

^2,47 100 %  25,5 %.

9,7

Задача № 3.

По нижеследующим данным определите: а) среднюю урожайность озимой пшеницы; б) дисперсию (упрощенным способом); в) среднее квадратическое отклонение; г) коэффициент вариации.

Урожайность, ц/га	Посевная площадь, га ( f)	Середина интервала ( x)	Сокращенные веса в 50 раз ( f)	xf	x2 f
А	1	2	3	4	5
20-22	150	21,0	3	63,0	1323,00
22-25	50	23,5	1	23,5	552,25
25-30	100	27,5	2	55,0	1512,50
30-40	200	35,0	4	140,0	4900,00
Итого	500	Х	10	281,5	8287,75

Решение:
а) средняя урожайность:
_{x } xf

_ f