Статистика задачи. Статистика Решебник. Учебнометодическое пособие по дисциплине Статистика составлено по разделу Теория статистики

• Название: Учебнометодическое пособие по дисциплине Статистика составлено по разделу Теория статистики
• Анкор: Статистика задачи
• Дата: 04.06.2022
• Размер: 359.42 Kb.
• Имя файла: Статистика Решебник.docx
• Тип: Учебно-методическое пособие; #569460
• страница: 8 из 23

 ^281,5  28,15 (ц/ гa);

10

б) так как интервал группировки неравный, дисперсия находится упрощенным способом:

 ²  x²  (x)²

_ x² f

 <sub> f

 ( </sub> xf

_ f
)² 

8287,75


10

 28,15² 

 828,775  792,422  36,35

в) среднее квадратическое отклонение: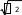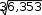
    6,03 _ц/га;

г) коэффициент вариации: ^V

 ^ 100% 

x

6,03


28,15
100%  21,4%.

Задача № 4.

По нижеследующим данным о группировке магазинов по размеру товарооборота определите: а) среднюю величину товарооборота на один магазин по каждому району и в целом по всей совокупности магазинов; б) дисперсию признака по каждому району и в целом по всей совокупности магазинов; в) среднюю из групповых дисперсий; г) межгрупповую дисперсию; д) результаты проверьте правилом сложения дисперсий; е) для характеристики влияния на вариацию территориального признака рассчитайте эмпирический коэффициент детерминации и корреляционное отношение.

Группы магазинов по величине товарооборота, тыс. руб.	Число магазинов
	Район А	Район Б	Итого
А	1	2	3
400-600	6	3	9
600-800	17	20	37
800-1000	35	22	57
1000-1200	33	40	73
1200-1400	9	25	34
Итого	100	110	210

Решение:

Промежуточные расчеты делаем в табличной форме:

Группы магазинов по величине товарооборота, тыс. руб.	Число магазинов
	Район А ( f1 )	Район Б ( f2 )	Итого ( f)
А	1	2	3
400-600	6	3	9
600-800	17	20	37
800-1000	35	22	57
1000-1200	33	40	73
1200-1400	9	25	34
Итого	100	110	210

Cере- дина интер- вала (x)	x  AA 900		x A	 x A   f1  i 	 x A   f2  i 	 x  A   f  i 	 x  A2   f1  i 	 x A2   f2  i 	 х А   f  i 
			i i 200
4	5	6		7	8	9	10	11	12
500	- 400	-2		-12	-6	-18	24	12	36
700	- 200	-1		-17	-20	-37	17	20	37
900	-	-		-	-	-	-	-	-
1100	200	1		33	40	73	33	40	73
1300	400	2		18	50	68	36	100	136
Итого	Х	X		22	64	86	110	172	282

а) Тогда средний товарооборот определяется по методу моментов:

x m₁  i А _,



_ x A_{ f}

где

 


i

f
_m1 _ _ 

Средний товарооборот одного магазина в районе А:

x₁ 

22


100
 200  900  0,22  200  900  944 тыс. руб.

Средний товарооборот одного магазина в районе Б:

x₂ 

64


100
 200  900  0,58 200  900  1016 тыс. руб.

Средний товарооборот одного магазина по всей совокупности магазинов:

_x 86

210

 200  900  0,41 200  900  982 тыс. руб.


_ x A_2

б) ^2

 i²  m

• 
  ^{m2 }, где
  

m₂ 

  ^f


i
 

_ f

1

2
Дисперсия по району А:

 ²  200² ^110  0,22^{2 }  42064




^{1 }100 ^

Дисперсия по району Б:

 ²  200² ^172  0,58^{2 }  49088




^{1 }100 ^

Общая дисперсия:

 ²  200² ^{ 282}  0,41^{2 }  46992




^ 210 ^

в) средняя из внутригрупповых дисперсий:

_ 2

 ² f

  ² f

42064 100  49088110

9606080

 ² 

ⁱ _1 1 2 2 _

  45743

i
i _{ f}

 ^f1

 _ f₂

210

210

г) межгрупповая дисперсия:

 ² 

_x_i

• 
  x2 f
  

_ x₁

 x² _ f

 x₂

• 
  x² f
  



2


i

1
^{ f}i ^{ f}1 ^{  f}2




944  982²100  1016  982²110 210

271560


210

 1293

д) правило сложения дисперсий:

i
 ²  ²  ²

 45743 193  47036 _{, т.е. 2 ,}
полученная по методу

моментов

46992  47000

равна

 ² ,

полученной как сумма средней из

групповых дисперсий и межгрупповой дисперсии

^{47036  47000} .

е) эмпирический коэффициент детерминации:

 ²  ^2

_ 2