Статистика задачи. Статистика Решебник. Учебнометодическое пособие по дисциплине Статистика составлено по разделу Теория статистики
 Скачать 359.42 Kb. Скачать 359.42 Kb.
|
0,543n(n1) 15 15 1 15 14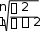 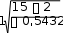 Проверяем значимость коэффициента Кендалла по t критерию Стьюдента: Проверяем значимость коэффициента Кендалла по t критерию Стьюдента:tp 0,543 2,332 При уровне значимости 0,05 tT 2,145 . Следовательно, значимость подтверждается т.к. tp tT Задача № 5. По данным о стоимости основных фондов и объеме произведенной продукции определите уравнение связи и тесноту связи:
Решение: Связь предполагается линейная, уравнение прямой  yx a0 a1 x Решаем систему уравнений методом наименьших квадратов: n a0 a1 x y, 2 a0 x a1 x xy 10 a0 55a1 55a0 385а1 445, 2907 a0 13,8; a1 5,6; yx13,8 5,6x Коэффициент регрессии a1 свидетельствует о том, что при увеличении объема основных фондов на 1 млн. руб. количество произведенной продукции увеличится на 5,6 млн. руб. Тесноту связи определяем по линейному коэффициенту корреляции: 2907 55 446r xy x y 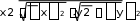 xy x y xy x y |
| № № с/х пред- прият ия | Внесено удо- бре- ний на 1 га, ц ( x) | Уро- жай- ность ц\га ( y) | x2 | x3 | x4 | xy | x2 y | yx | y2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0,4 | 14 | 0,16 | 0,064 | 0,0256 | 5,8 | 2,24 | 14,98 | 196 |
| 2 | 0,5 | 16 | 0,25 | 0,125 | 0,0625 | 8,0 | 4,00 | 17,11 | 256 |
| 3 | 0,5 | 19 | 0,25 | 0,125 | 0,0625 | 9,5 | 4,75 | 17,11 | 361 |
| … | … | … | … | … | … | … | … | … | … |
| 29 | 1,4 | 32 | 1,96 | 2,744 | 3,8416 | 44,8 | 62,72 | 30,02 | 1024 |
| 30 | 1,5 | 30 | 2,25 | 3,375 | 5,0625 | 45,0 | 67,50 | 30,77 | 900 |
| Итого | 30,0 | 750 | 32,90 | 38,484 | 47,0762 | 791, 1 | 899,9 5 | 750,0 | 2040 0 |
Решение:
Произведем выравнивание по параболе второго порядка:

yx a0
a1
x a2
x2 ;
Решаем систему нормальных уравнений:
n a0
a1 x a2
x2
y,
2
a0 x a x a
2
x3 xy,
2
3
4
а0 x
a1 x
a2 x
x2 y
30а0 30а1 32,90а2
750,00,
30а0 32,90а1 38,484а2 781,10,
0
32,90а 38,484а 47,0762а
1 2
899,95
Решение этой системы уравнений методом наименьших квадратов дает следующие значения параметров:
a0 5,086
a1 27,511
a2 6,927
0
y 5,086 27,511x 6,927x2
Так как связь криволинейная, для определения тесноты связи используется корреляционное отношение:
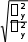 Э ,
Э ,y
где общая дисперсия признака y, 2
___
y2 ( y)2 ¸
а межгрупповая дисперсия:
 2
2 ( yi
y)2

i
y f
Общая дисперсия определятся по исходным (не сгруппированным) данным, т.е.
___
20400 750 2
y
2 y2 ( y)2
30
30
680 625 55
Для нахождения межгрупповой дисперсии необходимо произвести группировку предприятий по количеству внесенных минеральных удобрений.
Результат группировки данных по количеству внесенных минеральных удобрений на 1 представлен в нижеследующей таблице:
| Группы с/х предприятий по количеству внесенных минеральных удобрений на 1 га, ц. | Количество предприятий | Средняя урожайность, ц/га |
| А | 1 | 2 |
| 0,3 – 0,5 | 4 | 14 |
| 0,5 – 0,7 | 5 | 16 |
| 0,7 – 0,9 | 9 | 32 |
| 0,9 – 1,1 | 6 | 29 |
| 1,1 - 1,3 | 4 | 28 |
| 1,3 и более | 2 | 20 |
В данной задаче факторный признак количество минеральных
удобрений
, а результативный – урожайность
) . Межгрупповая
дисперсия
2
( yi
y)2
;
2 вычисляем по данным группировки в
i
y f y
вышеизложенной таблице
___ 2


y
i


 – средняя урожайность в каждой группе, то
– средняя урожайность в каждой группе, то есть
естьy1 14 ;
y2 16 ;
y3 32 ;
y4 29 ;
y5 28 ;
y6 20 .
Общая средняя признака
y 750 25 ,
30
fi – число предприятий в
каждой группе,
fi 30
заводам.
 Составим расчетную таблицу:
Составим расчетную таблицу:| yi | fi | ( yi y) | ( y y)2 i | ( y y)2 f i i |
| 1 | 2 | 3 | 4 | 5 |
| 14 | 4 | -11 | 121 | 484 |
| 16 | 5 | -9 | 81 | 405 |
| 32 | 9 | 7 | 49 | 441 |
| 29 | 6 | 4 | 16 | 96 |
| 28 | 4 | 3 | 9 | 36 |
| 20 | 2 | -5 | 25 | 50 |
| Итого | 30 | Х | Х | 1512 |