Пономаренко-Математика. Кратные интегралы. Учебное пособие предисловие данное учебное пособие предназначено для студентов немате

• Название: Учебное пособие предисловие данное учебное пособие предназначено для студентов немате
• Дата: 27.03.2023
• Размер: 0.93 Mb.
• Имя файла: Пономаренко-Математика. Кратные интегралы.docx
• Тип: Учебное пособие; #1019168
• страница: 4 из 17

Вычисление двойного интеграла

Двойной интеграл вычисляется обычно при помощи сведения его к повторному интегралу того или иного вида.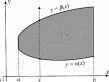




Рис.5

Теорема 1. Если:

1. 
   
   ∫∫
   область интегрирования (S) ограничена снизу кривой с уравне- нием y= α(x), сверху y= β(x), с боков прямыми x = a, x = b, причем функции α(x), β(x) непрерывны на сегменте [a,b] (рис. 5);
   
2. 
   существует f(x,y) dxdy;
   

(S)

3. 
   для любого x, x∈ [a,b], существует
   

β(x)

∫
α(x)

f(x,y) dy, то

b ^β(x)

∫∫ f(x,y) dxdy= ∫ dx∫ f(x,y) dy,

где

(S)


∫

_∫b
β(x)

a
_∫b⎛

α(x)

∫
β(x) ^⎞

dx

^a α(x)

f(x,y) dy

def

=

a

⎝⎜ α(x)

^{f(x,y) dy⎟}⎠ ^dx.

Последний интеграл называется повторным. Внутренний интеграл вычисляется при постоянном значении xиз [a,b].

Теорема 2. Если:

1. 
   область интегрирования (S) ограничена снизу прямой с урав- нением y = c, сверху y = d, слева кривой с уравнением x = μ(y), справа x = ν(y), причем функции μ, ν непрерывны на сегменте [c, d] (рис. 6);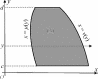
   

∫∫
Рис.6

2. 
   существует f(x,y) dxdy;
   

(S)
ν(y)

3. 
   для любого y, y∈ [c,d], существует
   

μ(∫y)

f(x,y) dx, то

∫∫

∫

∫
d ^ν(y)

(S)

f(x,y) dxdy=

c

dy

μ(y)

f(x,y) dx,

где


∫

_∫d
ν(y)

_∫d^{⎛ ν}_∫^{(y) ⎞}

dy

^c μ(y)

f(x,y) dx

def

=

c

⎜⎝μ(y)

^{f(x,y) dx⎟}⎠ ^dy.

∫∫
Интеграл в правой части последнего равенства также называ- ется повторным. Внутренний интеграл находится при постоянном значении yиз [c,d].

Пример 1. Вычислить интеграл I= (x+ 2y) dxdy, где (S) —

(S)

область, ограниченная линиями с уравнениями y= x², y= x.

Решение.Вычислим интеграл Iдвумя способами.

1. 
   Сведем рассматриваемый интеграл к повторному, используя теорему 1. Область интегрирования (S) проектируется на ось Ox в сегмент [0,1] (рис. 7). Поэтому пределы интегрирования во внешнем (левом) интеграле повторного интеграла равны 0 и 1.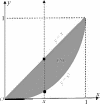
   

Рис.7
Внутренний интеграл находится при фиксированном (постоян- ном) значении x. Возьмем какую-нибудь точку xиз сегмента [0,1] и проведем через нее прямую, параллельную оси Oy. Рассмотрим ось, совпадающую с этой прямой и направленную так же, как ось Oy. Эта ось входит в область интегрирования, пересекая парабо- лу y = x², выходит, пересекая прямую y = x (см. рис. 7). Поэтому пределы внутреннего интеграла равны x² и x соответственно. (Это означает, что при фиксированном x переменная y изменяется от y= x² до y= x.)

Имеем


∫

∫
1 x

I= dx

⁰ x²


(x+ 2y) dy=

1




(xy+ y²) y=x


∫

^{. 2}y=x

.
0


dx=

_.

=


0


(x² + x²) − (x³ + x⁴)


dx=


0


(2x² − x³ − x⁴) dx=

_∫1 _∫1

= x³ x⁴


2

−

1

−
3 4

1 _x5

5

1 ₂


=
._{0 3}

1 1 13

— ₄ − ₅ = ₆₀ .

Рис.8

2. 
   Используем теорему 2. Спроектируем область интегрирова- ния (S) на ось Oy. Получим снова сегмент [0, 1]. Пределы внешнего интегрирования, как и ранее, равны 0 и 1. Для определения преде- лов внутреннего интегрирования возьмем точку y из сегмента [0, 1] и зафиксируем ее. Ось, проходящая через эту точку и параллель- ная оси Ox, входит в область интегрирования, пересекая прямую x= y, выходит, пересекая ветвь той же параболы (рис. 8) Отсюда
   

^.x=y
₁ ^√y₁




I= ∫ dy∫ (x+ 2y) dx= ∫ (0.5x² + 2xy)^.x=√y dy=

0 y0


∫
1

1 3 1

= ₂ y+ 2y² − ₂
y² − 2y²
dy=

.




= 4 ⁺ 5 ⁻ 6 ⁼ 60 ^.



₄ + ₅ y² − ₆ y

=
y² 4 5


₅ 3 _.1

1 4 5 13

Пример 2. Изменить порядок интегрирования в интеграле I=


∫

dx


1


1−^√4x−x²−3


f(x,y) dy.


∫
3 1

Решение.Интеграл I— результат сведения к повторному двой-


∫∫
ного интеграла f(x,y) dxdy, где (S) определена пределами инте-

(S)


√
грирования повторного интеграла:




(S) = {(x,y)| 1 ≤ x≤ 3,1 − 4x− x² − 3 ≤ y≤ 1}.


— −

— − −
Уравнение y = 1 ^√4x x² 3 — уравнение нижней половины окружности (x 2)²+(y 1)² = 1 (рис. 9). Спроектируем область ин-


√
тегрирования (S) на ось Oy(рис. 10). Решим последнее уравнение

(x− 2)² + (y− 1)² = 1 относительно x: x= 2 ± 2y− y².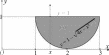






Рис.9 Рис.10
Теперь применим теорему 2. Получим

∫
1

I= dy

2+^√2y−y²

∫ f(x,y) dx.

⁰ 2−^√2y−y²
Пример 3. Изменить порядок интегрирования в интеграле


dx

f(x,y) dy.
_∫1 _∫2x


0


x




Решение.Интеграл получен в результате сведения к повторному


∫∫
двойного интеграла f(x,y) dxdy, где область интегрирования

(S)
(S) = {(x,y)| 0 ≤ x≤ 1,x≤ y≤ 2x}

определена пределами интегрирования данного повторного инте- грала (рис. 11).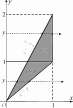

Рис.11 Рис.12
Спроектируем область интегрирования (S) на ось Oy(рис. 12). Решим уравнения y = x, y = 2xотносительно x: x = y, x = ^y.

2

Правая граница области интегрирования состоит из отрезков двух


, ,

y
прямых x = yи x= 1. Одним уравнением эту часть границы запи- сать не удастся.


1

2

2
Введем области (S) = (x,y)| 0 ≤ y≤ 1, ≤ x≤ y и (S ) =


1

2
,(x,y)| 1 ≤ y≤ 2,^y≤ x≤ 1,. Так как (S) = (S) ∪ (S), то




∫∫

(S)

^(S1⁾
по свойству аддитивности ^∫∫ f(x,y) dxdy = ^∫∫ f(x,y) dxdy +

f(x,y) dxdy. Сведя каждый из интегралов в правой части по-

^(S2⁾

следнего равенства к повторному, имеем

∫∫
(S)
1 ^y


∫

∫
f(x,y) dxdy= dy

₀ y

2
2


∫
f(x,y) dx+

1
1


∫
dy f(x,y) dx.

y

2

∫∫
Замечание. По аналогии с определенным интегралом Рима- на доказывается утверждение о геометрическом смысле двойного интеграла: двойной интеграл f(x,y) dxdyравен алгебраической

(S)

сумме объемов тел, ограниченных поверхностью z = f (x, y), плос- костью Oxy и цилиндрической поверхностью с образующими, па- раллельными оси Oz, проходящей через границу области интегри- рования (S); при этом объемы тел, расположенных над плоскостью

−
Oxy, берутся в этой сумме со знаком «+», под плоскостью Oxy— со знаком « » (предполагается, что ось Oz направлена снизу вверх). Это замечание часто удобно использовать при нахождении объ-

емов различных тел.

Задание. Из задачника [4] решить примеры № 3465, 3478, 3481,

3488–3494, 3498–3504, 3506–3510, 3562, 3564, 3565, 3601.