∫∫
Замена переменных в двойном интеграле
Замена переменных интегрирования в интеграле f(x,y) dxdy
(S)
состоит в переходе от переменных xи yк новым переменным uи
v, связанным со старыми соотношениями
x= x(u,v),
y= y(u,v).
(4)
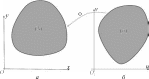 Рис.13 Рис.13
При этом система (4) представляет собой отображение Φ = x(u,v) некоторой замкнутой ограниченной области ( σ) в плос- y( u,v) кости O1uvна замкнутую ограниченную область ( S) в плоскости Oxy(рис. 13). Если выполняются условия:
отображение (4) взаимно однозначно;
функции x(u, v), y(u, v) в (4) непрерывно дифференцируемы в (σ);
якобиан отображения (4)
..
∂y..
.
∂x
J(u,v) = ∂u
∂y
∂u
∂x
.
∂v= 0 в (σ),
∂v
то имеет место формула4
∫∫
(S)
f(x,y) dxdy=
∫∫
(σ)
f(x(u,v),y(u,v)) |J(u,v)| dudv.(5)
При этих условиях существует обратное отображение Φ −1 : (S) −→ (σ),Φ−1 = u( x,y) , т. е. u= u( x,y) ,(6)v( x,y) v= v( x,y) .
Φ
Далее, ∀ N ∈ ( σ), N( u,v) −→ M( x( u,v) ,y( u,v)), M ∈ ( S); u, vназываются криволинейнымикоординатамиточки M 5. Кри- вые u(x, y) = const, v( x, y) = const называются координатнымилиниями. Через каждую точку M области ( S) проходят две коор- динатные линии u = const, v = const. (Аналогично для каждой точки N∈ ( σ).) 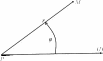
Рис.14Во многих задачах в качестве криволинейных координат часто используются полярные координаты r, ϕ, которые определяются следующим образом (рис. 14). Вводится полярная ось ( l) с началом в полюсе (точка P ). Из Pпроводится луч PM в точку M ( M — лю- бая точка плоскости, не совпадающая с точкой P ). Первая коорди- ната r— полярный радиус-вектор точки M— задается равенством r= PM, вторая коо рдина та ϕ— угол ме жду вектором P−−M→ и ос ью
∞
( l), 0 ≤ r< + , 0 ≤ ϕ<2 π. При r= 0 угол ϕне определен, для него можно задать любое значение. 4 Доказательство этого утверждения желательно изучить самостоятельно, используя учебники, например [1]. 5 Криволинейные координаты u,vзаписывают так же, как и декартовы (в круглых скобках рядом с точкой: M( u,v)).
Во многих случаях полярные координаты связывают с декарто- выми. Если полярную ось совместить с неотрицательной полуосью Ox прямоугольной декартовой системы координат Oxyтак, чтобы полюс P совпал с точкой O, то получим формулы
x = r cos ϕ,y= rsin ϕ.
Найдем якобиан преобразования:
∂x∂x
. . . .
.
∂y
. ∂r
∂y
∂ϕ.
sin ϕ rcos ϕ.
J(r,ϕ) = ∂r
∂ϕ. = .cos ϕ −rsin ϕ. = r.
Формула (5) запишется в виде
∫∫
∫∫
f( x,y) dxdy= f( rcos ϕ,rsin ϕ) rdrdϕ. (7) ( S) ( σ) Приведем примеры замены переменных.
x
(S)
Пример_1.'>Пример 1. Вычислить интеграл I= ∫∫ y 2 ( x2 + 2) dxdy, ( S) расположена в 1-м координатном квадранте и ограничена линиями с уравнениями xy= 1, xy= 2, y= x, y= 3 x(рис. 15). 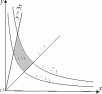
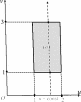
Рис.15 Рис.16
Решение. Введем новые переменные интегрирования u и v
y
по формулам u= xy. Область (S) перейдет в область (σ) =
v=
x
⎧
{( u,v)| 1 ≤ u≤ 2 , 1 ≤ v ≤ 3} (рис. 16). Выразим x и y через 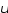
uи v: ⎨x= v. Найдем якобиан преобразования:
⎩y= √uv
. ∂x
∂x.
1
1 u.
J( u,v) = ∂u ∂v ∂v 2 √uv− 2
= .
. v3 1 1 1
.
= + = .
∂y∂y
. .
. 1 v
1 u. 4v 4v 2v
.
∂u ∂v
. 2 u
2 v .
Вычиcлим далее интеграл I.
I = ∫∫
v2 u+ 2 1
dudv=
1 ∫2
(σ)
∫
−
∫∫
1
.
=
2
1
du
v=1
du=
∫3
v 2v
(u+ 2v)dv=
2
1
(uv+ v2)
1 ∫2
.v=3
2
1
= 2 (3u+9 − u− 1)du=
1
2
∫
(u+ 4)du=
1
u2
+ 4u
2
2 11
.
=
.
.1 2
Пример 2. Вычислить интеграл I= ( x2 + 3 y2) dxdy, где ( S) ( S) ограничена частью лемнискаты Бернулли ( x2 + y2) 2 = 4( x2 y2), 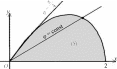 лежащей в первом квадранте, и осью Ox(рис. 17). Рис.17
Решение.Введем полярные координаты r,ϕ: x= rcos ϕ.
y= rsin ϕ
√
Уравнение лемнискаты Бернулли запишется в виде r =
cos 2ϕ.Точка (r,ϕ) находится в области интегрирования (S), ес-
4
ли 0 ≤ ϕ≤ π, 0 ≤ r≤ 2√cos 2ϕ. Поэтому
∫
π
4
I= dϕ
0
π
2√cos 2ϕ
∫
r2(1+2 sin2 ϕ) · rdr=
0
π
∫
4
(2−cos 2ϕ)dϕ
0
.
4 r=2
cos 2ϕ
.
2
π
2√cos 2ϕ
∫
r3dr=
0
(2 − cos 2ϕ) r r=0 dϕ= 4
0
=
4
1 ∫4  √ ∫4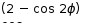 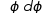
∫
∫
π π
4 4
= 4 (1+ cos 4ϕ)dϕ− 4
0 0
∫
π
4
ππ
cos3 2ϕdϕ=
= 4 · 4
+ sin 4ϕ| 4 − 2
0
0
(1 − sin2 2ϕ)d(sin 2ϕ) =
2
= π+0 − 2 · 1+ 3
sin3
π
0
4
3
2ϕ. 4 = π− .
Задание. Из задачника [4] решить примеры № 3525–3527, 3530, 3539, 3540, 3602–3605. |
 Скачать 0.93 Mb.
Скачать 0.93 Mb.