Учебное пособие управляющего типа Агарков В. И., Бутева Л. В. Грищенко С. В. Донецк Донгму, 2006. 277 с
 Скачать 3.03 Mb.
|
Таблица 5Распределение больных с ОРЗпо длительности нетрудоспособности
Способ моментов. Этот более простой способ вычисления средней арифметической взвешенной величины применяется при большом числе наблюдений и вариантах, выраженных большими числами. Он основан на том, что алгебраическая сумма отклонений отдельных вариант вариационного ряда от средней арифметической равна нулю, т.е. Σ(– d)=Σ(+ d), где d – истинные отклонения варианты от истинной средней арифметической величины. Данное свойство средней используется при проверке правильности ее расчетов. Если сумма отклонений вариант от средней равна нулю, то можно сделать вывод, что средняя вычислена правильно. Например, возьмем следующие пять вариант: 2, 4, 4, 6, 9. Их средняя М=(2+4+4+6+9):5=5. Выпишем отклонения каждой варианты от средней и просуммируем их:
Сумма отклонений равна нулю, значит средняя рассчитана правильно. В практике, однако, случается, что сумма всех положительных и отрицательных отклонений вариант от средней арифметической не равняется нулю, и это не должно смущать исследователя: такие случаи указывают на погрешности, допущенные при округлении дробных чисел. Если условная средняя (А), используемая при расчете по способу моментов равна истинной средней арифметической величине (М), то сумма отклонений вариант от условной средней будет равна нулю, т.е. при А=М сумма отклонений равна нулю, при А>М, Σd будет отрицательной величиной, наконец при А<М, Σd будет положительной величиной. Средняя арифметическая по способу моментов определяется по формуле:  ,где: А – условно принятая средняя; а – условное отклонение каждой варианты от условной средней (V – А); i – величина интервала, т.е. разность между соседними вариантами. Следует обратить внимание на то, что если величина интервала (i) между соседними вариантами равна единице, формула расчета средней арифметической по способу моментов имеет следующий вид:  Именно такая формула представлена во многих учебниках. Если величина интервала меньше или больше единицы, то для упрощения расчетов разность между соседними вариантами принимают за единицу, фактическое же значение этой разности вводится в последующем в формулу, и она приобретает следующий вид: Причем условные отклонения (а) (в табл. 6, графа 7) в этом случае не рассчитываются как разность V–А, а приравниваются условно порядковым номерам в порядке возрастания вариант вариационного ряда: +1, +2, +3 и т.д. (или по мере их уменьшения: –1, –2, –3 и т.д.) (табл. 6, пример 2). Примеры расчета средней арифметической взвешенной величины по способу моментов Пример 1. В результате измерения длины тела (в см) при рождении у 47 девочек были получены следующие данные: 48, 51, 53, 49, 51, 53, 51, 48, 52, 51, 53, 49, 50, 53, 48, 52, 50, 52, 50, 52, 50, 51, 52, 53, 47, 52, 48, 48, 50, 52, 46, 46, 54, 55, 56, 48, 52, 52, 51, 53, 53, 48, 50, 54, 48, 50, 50. Пример 2. Результаты измерения температуры тела у 22 новорожденных были следующими: 37,0; 36,6; 37,2; 36,9; 36,6; 37,0; 37,1; 36,8; 37,0; 36,9; 37,2; 37,1; 36,8; 36,7; 36,9; 36,6; 37,0; 36,9; 36,7; 36,8; 37,0; 36,6. Используя методику расчета средней арифметической взвешенной по способу моментов, определим среднюю длину тела у девочек при рождении и среднюю температуру тела у новорожденных. Для этого необходимо: 1. Построить вариационный ряд, расположив варианты в возрастающем или убывающем порядке с соответствующими им частотами. В нашем примере варианты расположены в убывающем порядке (табл. 6, графы 1, 2). Таблица 6 Распределение девочек при рождении по длине и температуре тела
2. Выбрать условную среднюю (А). За условную среднюю можно взять любую варианту ряда, но чаще всего принимают наиболее часто встречающуюся варианту. В примере №1 наиболее часто встречается варианта 52, она встречается у 9 девочек, т.е. А=52. В примере №2 условная средняя равна 37°С. 3. Определить условные отклонения (графа 3). Условное отклонение (a) вычисляется как разность между каждой вариантой и условной средней (V–А). Вычисленные значения условных отклонений занесем в графу 3 табл. 6 с учетом алгебраических знаков. Условным отклонениям (а) в графе 7 приданы порядковые номера. 4. Перемножить значение каждого условного отклонения с соответствующей частотой (ар), результаты занести в графу 4 и 8 табл. 6 и найти их сумму (Σар). 5. Подставить все значения в формулы:  смВ формуле расчета М1 величина интервала (i) не используется, т.к. разность между соседними интервалами равна единице. В формулу для расчета М2 введена величина интервала (i), равная 0,1 (36,7°С – 36,6°С=0,1). Т.к. для упрощения расчетов разность между соседними вариантами была принята за единицу, а условным отклонениям (графа 7 табл.6) приданы порядковые номера с учетом алгебраических знаков:  °СВыводы. 1. Длина тела у девочек при рождении составила в среднем 50,74 см. 2. Средняя температура тела у новорожденных составила 36,9°С. Средняя арифметическая взвешенная по способу моментов может быть вычислена и в случае сгруппированного (интервального) вариационного ряда. Методика расчета средней арифметической по способу моментов в сгруппированном ряду такая же, как и в не сгруппированном ряду, за некоторым исключением. В сгруппированном ряду расчет средней арифметической начинается с определения середины интервала (центральной варианты). Центральная варианта в непрерывных вариационных рядах определяется как полусумма наименьших значений двух соседних групп. Например: Группы вариант Центральная варианта 10,0 – 11,9  12,0 – 13,9  14,0 – 15,9  и т.д. и т.д. Центральная варианта в дискретных вариационных рядах (варианты выражены целыми числами) определяется как полусумма крайних значений каждой группы. Для данных табл. 3, графа 4, центральными вариантами будут  ,  и т.д. В сгруппированном ряду для еще большего упрощения расчетов разность между соседними вариантами принимают за единицу, фактическое же значение этой разности (i)вводится в последующем в формулу и она приобретает следующий вид:  В качестве примера рассчитаем среднюю частоту пульса перед экзаменом у студентов-медиков (по способу моментов), используя данные табл. 3, в которой сгруппированный ряд был составлен нами ранее. В табл. 7 сведены некоторые данные табл. 3 и определены центральные варианты (графа 3), как указывалось выше, определены условные отклонения (графа 4), причем, для упрощения расчетов разность между соседними центральными вариантами принята за 1, вместо действительной разности, равной 3 (81 – 78), что будет учтено в формуле расчета в дальнейшем. Средняя арифметическая взвешенная в сгруппированном ряду по способу моментов рассчитывается по формуле: , где:А – условная средняя (наиболее часто встречающаяся варианта, в нашем примере А=75, такая частота пульса встречалась у 16 студентов); i – величина интервала, т.е. разность между соседними центральными вариантами, в нашем примере i=3. Остальные обозначения известны. Таблица 7 Распределение студентов-медиков по частоте пульса перед экзаменом
Подставим все данные в формулу:  уд/минВывод. Частота пульса у студентов-медиков перед экзаменом составляла в среднем 71,9 (≈72) удара в минуту. Расчет средней арифметической величины, которая используется для характеристики количественного признака изучаемого явления, относится к методам «классической» вариационно-статистической обработки материалов медицинских и биологических исследований или, так называемым, параметрическим методам. Существуют и непараметрические методы статистической обработки, к которым относится расчет моды и медианы. Мода (Мо) – наиболее часто встречающаяся варианта в вариационном ряду. Для распределения, представленного в табл. 8, моде соответствует варианта, равная 10, она встречается чаще других – 6 раз. Таблица 8 Распределение больных по длительности пребывания на больничной койке (в днях)
Иногда точную величину моды установить трудно, поскольку в изучаемых данных может существовать несколько наблюдений, встречающихся «наиболее часто». Медиана (Ме) – непараметрический показатель, делящий вариационный ряд на две равные половины: в обе стороны от медианы располагается одинаковое число вариант. Например, для распределения, указанного в табл. 8, медиана равна 10, т.к. по обе стороны от этой величины располагается по 14 вариант, т.е. число 10 занимает центральное положение в этом ряду и является его медианой. Учитывая, что число наблюдений в этом примере четное (n=34), медиану можно определить таким образом:  Это означает, что середина ряда приходится на семнадцатую по счету варианту, которой соответствует медиана, равная 10. Для распределения, представленного в табл. 8, средняя арифметическая равна:  .Итак, для 34 наблюдений из табл. 8, мы получили: Мо=10, Ме=10, средняя арифметическая (М) равна 10,1. В нашем примере все три показателя оказались равными или близкими друг к другу, хотя они совершенно различны. Средняя арифметическая является результативной суммой всех влияний, в формировании ее принимают участие все без исключения варианты, в том числе и крайние, часто нетипичные для данного явления или совокупности. Мода и медиана, в отличие от средней арифметической, не зависят от величины всех индивидуальных значений варьирующего признака (значений крайних вариант и степени рассеяния ряда). Средняя арифметическая характеризует всю массу наблюдений, мода и медиана – основную массу. Такое совпадение показателей (Ме=Мо=М) характерно для распределений симметричных или приблизительно симметричных, характерной особенностью которых является симметричное распределение частот, причем наибольшее количество частот соответствует варианте, близкой по размерам к средней величине, а по обе стороны от нее частоты постепенно уменьшаются. Представим графически данные табл. 8 (рис. 1). 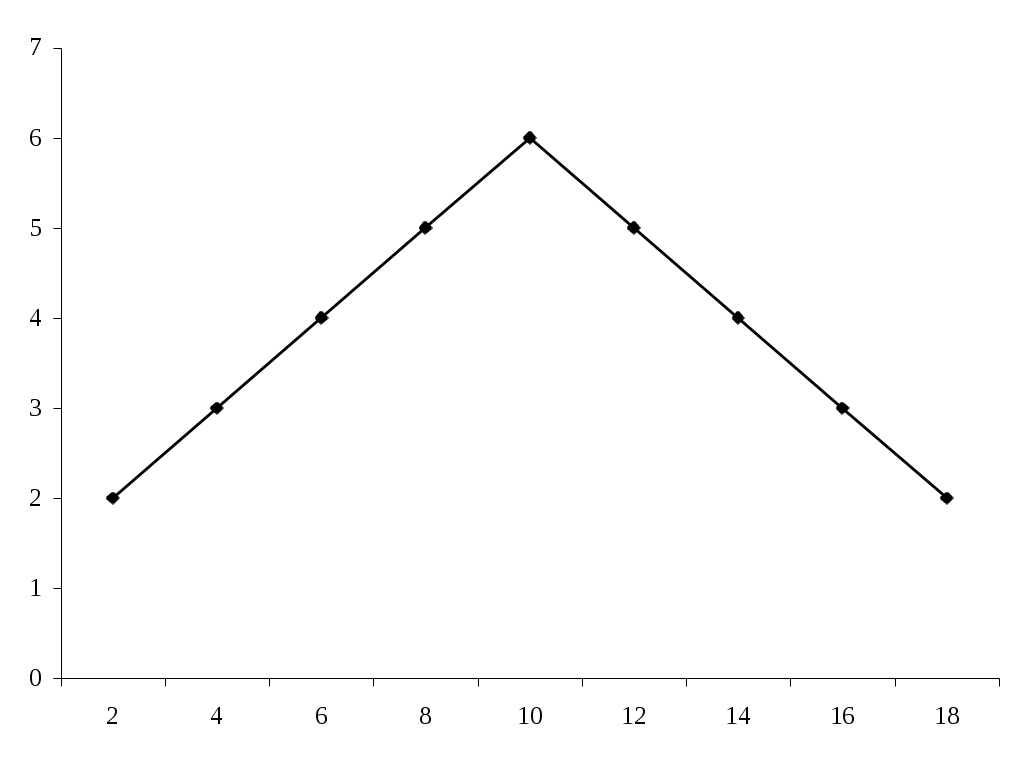 Рис. 1. Распределение больных по длительности пребывания на больничной койке (в днях) Распределения могут быть и не симметричными, в этом случае для характеристики данных необходимо пользоваться другими способами, что позволит обобщить основные особенности конкретной совокупности данных достаточно точно. Несмотря на то, что в предыдущем примере мода, медиана и средняя арифметическая оказались равными или близкими друг к другу, они различны по содержанию. Суть этих различий можно увидеть в табл. 9. Таблица 9 Содержание и применение средних величин
Медиана может быть определена и с учетом центральных вариант. Например, для распределения с вариантами 6, 9, 11, 14, 16, 17, 19, 21 медиана определяется с учетом центральных вариант. В данном случае центральными вариантами являются 4-я и 5-я. Медиана будет равна:  При нечетном числе наблюдений медианой является варианта, имеющая в вариационном ряду порядковый номер (n +1)/2. Учитывая, что на величину моды и медианы, в отличие от средней арифметической, не оказывают влияние значения крайних вариант и степень рассеяния ряда, применение моды и медианы целесообразно в тех случаях, когда при небольшом числе наблюдений крайние варианты велики и в значительной мере определяют величину среднеарифметической. Так, например, изучались сведения о продолжительности заболевания всего лишь у 11 больных. Они распределились следующим образом (табл. 10). Таблица 10 Сведения о продолжительности заболевания (в днях)
Мы видим, что у одного из больных заболевание продолжалось более длительно, чем у остальных (46 дней). Данные этого одного больного в большей мере определяют величину средней арифметической, которая равна 9 дням (  ) и, по сути дела, не дает правильного представления о длительности заболевания. Врача интересует так называемая обычная, наиболее часто встречающаяся длительность заболевания, а не отвлеченная средняя ее величина. Поэтому в этом случае мода является более приемлемой, чем средняя арифметическая величина. Продолжительность заболевания в 6 дней наблюдалась наиболее часто, она является модой для данного ряда.Средняя величина может быть рассчитана не только на основе абсолютных данных, но и среди показателей. При одинаковых числах наблюдений ее находят как среднюю простую, т.е. достаточно суммировать размеры показателей и затем поделить на их число. При разных числах наблюдений среднюю величину среди показателей следует определять всегда как среднюю взвешенную. В своей практической деятельности врачи часто используют средние показатели работы различных учреждений. Однако использование в этих случаях обычных средних арифметических приводит к тому, что врач опирается не на опыт работы лучших, передовых коллективов, а на опыт «всех», т.е. и отсталых, плохо работающих. Поэтому рекомендуется применять не просто средние, а среднепрогрессивные показатели, основанные на опыте работы не всех, а только передовых учреждений, т.е. средняя прогрессивная вычисляется по той части вариант, которые характеризуют лучшие показатели. Рассмотрим суть средней прогрессивной на примере. Пример. Главный областной педиатр при анализе уровней детской смертности за прошлый год обнаружил в разных районах области довольно резкое их варьирование (табл. 11). Таблица 11 Уровень детской смертности в различных районах области
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
см
С°