Учебное пособие управляющего типа Агарков В. И., Бутева Л. В. Грищенко С. В. Донецк Донгму, 2006. 277 с
 Скачать 3.03 Mb. Скачать 3.03 Mb.
|
|
Коэффициент наглядности имеет целью представить сравниваемые, обычно самостоятельные, величины в более отчетливом, обозримом, наглядном виде. Разберем теперь методику расчета показателей наглядности. Показатель наглядности показывает во сколько раз или на сколько процентов изменяются (различаются) изучаемые величины не связанные друг с другом.
Показатели наглядности могут быть выражены и простым кратным соотношением, например, увеличение или уменьшение в 2-3 раза и т.п. Этот, в сущности, наиболее простой коэффициент получают путем преобразования ряда величин по отношению к одной из них, так называемой базисной, ил исходной (любой, не обязательно начальной – подчас наиболее яркой). За 100% можно принять не только одну из величин данного ряда, но даже отсутствующую в нем. Так, сравнивая материалы по данным здравоохранения за ряд последних лет (число врачей, инфекционных заболеваний и т.д.), в качестве базисной величины можно взять уровень дореволюционного (1913 г.), послевоенного (1946 г.), другого государства (США) и т.д. или принять за 100% среднюю из величин данного ряда. Сравнивать можно две или несколько статистических величин в статике, т.е. за один год, или в динамике за ряд лет. В коэффициенты наглядности можно преобразовывать не только абсолютные, но и относительные и средние величины. Например, необходимо сравнить заболеваемость корью детей в возрасте 0-4 лет в разных городах области (табл. 3). Таблица 3 Уровень заболеваемости корью детей в возрасте 0-4 лет в разных городах и области в отчетном году
Вывод. Заболеваемость корью детей в возрасте 0-4 лет в указанных городах значительно отличаются друг от друга. На уровне областных значений она находится только в городе С. Наиболее высокие показатели характерны для города А. Они на 50% выше среднеобластных значений. В то же время, в городе В. заболеваемость корью на 25% ниже, чем по области. Таким образом, изучение состояния здоровья населения или другого явления с помощью относительных величин позволяет определить не только размер, уровень изучаемого явления, но и определяющие его закономерности. В учреждениях здравоохранения постоянно осуществляется анализ результатов работы путем текущих или единовременных, сплошных или выборочных статистических исследований. Учитывая то, что относительные величины дают картину качественных признаков, в деятельности ЛПУ они используются для сравнения и сопоставления однородных величин за аналогичные периоды времени. Широкое применение полученные результаты находят при анализе показателей деятельности ЛПУ. Врач постоянно работает с относительными величинами, что позволяет ему оперативно следить как за состоянием здоровья населения своего района, города, области, так и за тенденциями и закономерностями развития здравоохранения в целом. ЗАДАНИЯ ДЛЯ КОРРЕКЦИИ УМЕНИЙ В соответствии с первой конкретной целью обучения по заданной теме – «Уметь определить возможность использования абсолютных величин или необходимость применения относительных коэффициентов» необходимо решить следующие задачи: Задача 1 На каждом курсе одного из вузов обучается по 800 студентов. В отчетном году среди них было зарегистрировано 105 заболеваний желудочно-кишечного тракта, которые распределились среди обучающихся следующим образом: 1 курс – 15 случаев; 2 курс - 20 случаев; 3 курс - 24 случая; 4 курс - 26 случаев; 5 курс - 20 случаев. Задача 2 В трех ведущих вузах города К. обучается немногим более 15 тыс. студентов. Среди них в отчетном году на медицинском осмотре было выявлено 165 случаев патологии со стороны органов пищеварения. В таблице представлены эти данные по вузам:
Задание. В какой из приведенных задач можно оценить заболеваемость студентов по абсолютным данным и почему? Ответ. Главной составной частью оценки заболеваемости является сравнение имеющихся данных между собой. В первой задаче сравнение можно провести по абсолютным величинам, так как среда, продуцирующая изучаемое явление (количество обучающихся студентов) одинакова на всех курсах. Во второй задаче возникает необходимость расчета относительных величин, в частности показателя интенсивности (частоты), так как количество обучающихся в указанных вузах различна. Если Вы дали правильный ответ, приступайте к отработке следующих умений: «Уметь выбрать соответствующий вид относительных величин, адекватный целям анализа и характеру имеющихся данных». «Уметь рассчитать относительные величины». Для этого решите следующую задачу: Задача 3 Городская больница №7 обслуживает 90 тысяч населения. В отчетном году в поликлинике больницы работало 340 врачей, в стационаре – 60 специалистов. Для оказания стационарной помощи населению закрепленной территории развернуто 950 коек. Среди обслуживаемого населения было зарегистрировано 112500 случаев заболеваний, в том числе 35000 болезней органов дыхания, из последних 22750 заболеваний носили хронический характер. В отчетном году уровни распространенности заболеваний среди населения выросли на 14% по сравнению с данными трехлетней давности. Примечание: В отчетном году распространенность заболеваний среди жителей области составила 1187,3 случаев на 1000 населения. Задания. 1. Укажите статистический характер показателя, который необходим для характеристики обеспеченности населения врачами и койками в указанной городской больнице. 2. Укажите статистический характер показателей, которые необходимы для определения: а) распространенности заболеваний среди населения; б) частоты болезней органов дыхания; в) уровня хронических болезней органов дыхания; г) удельного веса болезней органов дыхания среди всех заболеваний; д) доли хронических болезней среди всех болезней органов дыхания. 3. Укажите статистический характер показателя, который использован в задаче для сравнения распространенности заболеваний в отчетном году с данными трехлетней давности. 4. Укажите статистический характер показателя, который необходимо использовать для сравнения распространенности заболеваний в больнице со среднеобластными данными. 5. Рассчитайте следующие показатели: а) обеспеченность населения койками; б) распространенность заболеваний среди населения; в1) частоту болезней органов дыхания; в2) их удельный вес среди всех заболеваний; г1) уровень хронических болезней органов дыхания; г2) их долю среди всех болезней этого класса; д) обеспеченность населения врачами. 6. Сравните распространенность заболеваний в больнице со среднеобластными данными и сделайте выводы. Ответ. 1. – показатель соотношения; 2. (а, б, в) – интенсивный показатель; (г, д) – экстенсивный показатель; 3 – показатель наглядности; 4 – показатель наглядности; 5. а – обеспеченность населения койками составляет: б – распространенность заболеваний среди населения составляет: в1 – частота болезней органов дыхания составляет: в2 – удельный вес болезней органов дыхания среди всех заболеваний составляет: г1– уровень хронических болезней органов дыхания составляет: дыхания на 1000 населения; г2 – доля хронических болезней органов дыхания среди всех болезней этого класса составляет: д – обеспеченность населения врачами составляет: 6. Для сравнения показателей необходимо использовать показатель наглядности: 1187,3 случаев на 1000 населения (среднеобластной показатель) → 100 % 1250,0 случаев на 1000 населения (показатель по ГБ №7) →Х%, следовательно, Вывод. Распространенность заболеваний среди населения, обслуживаемого городской больницей №7 на 5,3% выше, чем по области. Если Ваши ответы совпали с нашими, приступайте к решению задачи, которая охватывает следующую цель темы: «Уметь оценить полученные данные и сделать выводы». Задача 4 В таблице приведены данные о числе умерших среди городского населения Н-ской области от травм за отчетный год. Данные приведены по возрастным группам. Имеются также данные о численности населения в этих возрастных группах и приведены некоторые относительные величины.
Задания. 1. Можно ли по абсолютным данным характеризовать повозрастную смертность от травм в конкретной ситуации? 2. Можно ли с помощью приведенных экстенсивных показателей утверждать, что самая высокая смертность от травм отмечается в возрастной группе 15-49 лет и почему? 3. Определите смертность от травм среди городского населения Н-ской области. 4. Сделайте выводы. Ответ. 1. Нет, т.к. все возрастные группы имеют разную численность. 2. Нет, т.к. экстенсивный показатель отражает только распределение случаев смерти от травм среди возрастных групп населения, а не показывает уровень смертности. 3. Для расчета смертности от травм среди городского населения Н-ской области используем интенсивный показатель:
т.е. 4. Выводы. 1) В отчетном году из каждых 10 тыс. городского населения погибло от травм примерно 3 человека. 2) Самые высокие уровни смертности от травм характерны для старшей возрастной группы (50 лет и старше), более низкие – среди детей. 3) Примерно каждый второй из общего числа умерших от травм входил в возрастную группу 15-49 лет и один из трех – в группу 50 лет и старше. Только немногим более 16% погибших были из числа детского населения. Приложение 1 Граф логической структуры темы «ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ, ИХ ИСПОЛЬЗОВАНИЕ В ЗДРАВООХРАНЕНИИ» 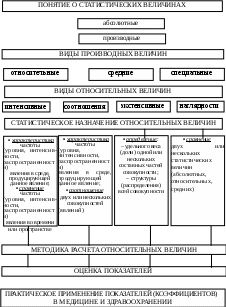                   Приложение 2 КЛАССИФИКАЦИЯ СТАТИСТИЧЕСКИХ ВЕЛИЧИН  ТЕМА 3.СРЕДНИЕ ВЕЛИЧИНЫ, ИХ ИСПОЛЬЗОВАНИЕ В ЗДРАВООХРАНЕНИИ Актуальность темы. В практической деятельности часто возникает необходимость обобщения больших массивов числовых данных. В этом случае определяют средний уровень изучаемого количественного признака. Средний уровень измеряют с помощью показателей, которые носят название средних величин. Врачи разных специальностей широко используют средние величины при: изучении физического развития различных групп населения (средний рост, вес, окружность грудной клетки и т.д.); характеристике физиологического состояния органов и систем организма человека (средняя частота пульса, средняя величина артериального давления, жизненной емкости легких, среднее содержание белка крови и т.д.); изучении закономерностей течения различных процессов в здоровом и больном организме; оценке эффективности применения лекарственных препаратов; гигиенической характеристике внешней среды (среднее содержание пыли и газов в воздухе производственных помещений и в атмосфере, средний уровень шума, вибрации и т.д.). Средние величины удобно сравнивать между собой и выявлять закономерности. Но если средние величины определены в неоднородных совокупностях, при малом числе наблюдений, они не только не вскрывают, но могут и затушевать истинную картину изучаемого явления. Так, за благополучными средними данными о здоровье населения или работе учреждений здравоохранения по области или городу в целом можно не заметить неудовлетворительные показатели здоровья населения или деятельности медицинских учреждений по городам, районам, соответственно. К средней обращаются всякий раз, когда надо исключить случайное влияние отдельных факторов, выявить общие черты, существующие закономерности. Учитывая изложенное, перед студентами поставлены следующие цели: ЦЕЛИ ЗАНЯТИЯ Общая цель: уметь применять средние величины для характеристики состояния здоровья населения и деятельности лечебно-профилактических учреждений. Общая цель достигается через конкретные умения: Определить целесообразность и необходимость расчета средних величин. Построить вариационный ряд и оценить его с помощью графического изображения. Рассчитать параметрические и непараметрические (мода, медиана) средние арифметические величины разными способами в зависимости от вида вариационного ряда. Рассчитать показатели колеблемости вариационного ряда (лимиты, амплитуду, среднее квадратическое отклонение, коэффициент вариации). Оценить вариационный ряд с помощью показателя асимметрии и сделать выводы. ИСТОЧНИКИ УЧЕБНОЙ ИНФОРМАЦИИ (рекомендуемая литература) Соціальна медицина та організація охорони здоров’я / Під ред. Вороненка Ю.В., Москаленка В.Ф. – Тернопіль: Укрмедкнига, 2000. – С. 52-62. Социальная гигиена и организация здравоохранения / Под ред. Серенко А.Ф., Ермакова В.В. – М.: Медицина, 1984. – С. 123-139. Руководство к практическим занятиям по социальной гигиене и организации здравоохранения / Под ред. Лисицына Ю.П., Копыта Н.Я. – М.: Медицина, 1984. – С. 72-86. Руководство по социальной гигиене и организации здравоохранения / Под ред. Лисицына Ю.П. – М.: Медицина, 1987. – Т.1. – С. 262-267. Граф логической структуры содержания темы (приложения 1-3). ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ ТЕМЫ Понятие о средних величинах, их характеристика. Принципы построения вариационного ряда. Виды и параметры вариационных рядов, их характеристики. Графическое изображение вариационного ряда. Методика расчета средних величин, в том числе средней арифметической величины различными способами в зависимости от вида вариационного ряда. Методика расчета показателей колеблемости вариационного ряда (лимита, амплитуды, среднего квадратического отклонения, коэффициента вариации, показателя асимметрии). Практическое применение средних величин в медицине и здравоохранении. ОСНОВНЫЕ ВОПРОСЫ И КЛЮЧЕВЫЕ ПОНЯТИЯ, НА КОТОРЫЕ СЛЕДУЕТ ОБРАТИТЬ ВНИМАНИЕ ПРИ ПОДГОТОВКЕ ТЕМЫ Как уже указывалось выше, для характеристики и оценки состояния здоровья населения и деятельности лечебно-профилактических учреждений врачи могут использовать как абсолютные данные, относительные показатели (интенсивные, экстенсивные, соотношения, наглядности), так и средние величины. Средние величины используются, если результаты исследований многочисленны, причем они могут быть представлены как в качественном, так и количественном выражении. Чаще мы имеет дело с результатами исследований, которые представлены в количественном выражении. Например, у 21 студентов-медиков исследовалась частота пульса (число ударов в минуту), которая составила: 80, 66, 74, 70, 64, 80, 80, 74, 68, 70, 74, 64, 68, 68, 66, 84, 84, 80, 70, 74, 84. Приведенные данные представляются на первый взгляд мешаниной из различных чисел, отличающихся друг от друга по значению. Для расчета средней частоты пульса у студентов-медиков необходимо имеющиеся числовые значения упорядочить, расположить в определенной последовательности, т.е. построить вариационный ряд. Вариационный ряд – это ряд числовых значений изучаемого признака, отличающихся друг от друга по своей величине и расположенных в определенной последовательности (в восходящем или убывающем порядке). Каждое числовое значение ряда называют вариантой (V), а числа, показывающие, как часто встречается та или иная варианта в составе данного ряда, называется частотой (р). Общее число случаев наблюдений, из которых вариационный ряд состоит, обозначают буквой n. Различие в значении изучаемых признаков называется вариацией. В случае если варьирующий признак не имеет количественной меры, вариацию называют качественной, а ряд распределения – атрибутивным (например, распределение по исходу заболевания, по состоянию здоровья и т.д.). Если варьирующий признак имеет количественное выражение, такую вариацию называют количественной, а ряд распределения – вариационным. Вариационные ряды делятся на прерывные и непрерывные – по характеру количественного признака, простые и взвешенные – по частоте встречаемости вариант. В простом вариационном ряду каждая варианта встречается только один раз (р=1), во взвешенном – одна и та же варианта встречается несколько раз (р>1). Примеры таких рядов будут рассмотрены далее по тексту. Если количественный признак носит непрерывный характер, т.е. между целыми величинами имеются промежуточные дробные величины, вариационный ряд называется непрерывным. Например: 10,0 – 11,9 12,0 – 13,9 14,0 – 15,9 и т.д. Если количественный признак носит прерывный характер, т.е. отдельные его значения (варианты) отличаются друг от друга на целое число и не имеют промежуточных дробных значений, вариационный ряд называют прерывным или дискретным. Используя данные предыдущего примера о частоте пульса у 21 студентов, построим вариационный ряд (табл. 1). Таблица 1 Распределение студентов-медиков по частоте пульса (уд/мин)
Таким образом, построить вариационный ряд – означает имеющиеся числовые значения (варианты) систематизировать, упорядочить, т.е. расположить в определенной последовательности (в восходящем или убывающем порядке) с соответствующими им частотами. В рассматриваемом примере варианты расположены в восходящем порядке и выражены в виде целых прерывных (дискретных) чисел, каждая варианта встречается несколько раз, т.е. мы имеем дело со взвешенным, прерывным или дискретным вариационным рядом. Как правило, если число наблюдений в изучаемой нами статистической совокупности не превышает 30, то достаточно все значения изучаемого признака расположить в вариационном ряду в нарастающем, как в табл. 1, или убывающем порядке. При большом количестве наблюдений (n>30) число встречающихся вариант может быть очень большим, в этом случае составляется интервальный или сгруппированный вариационный ряд, в котором для упрощения последующей обработки и выяснения характера распределения варианты объединены в группы. Обычно число групповых вариант колеблется от 8 до 15. Их должно быть не меньше 5, т.к. иначе это будет слишком грубое, чрезмерное укрупнение, что искажает общую картину варьирования и сильно сказывается на точности средних величин. При числе групповых вариант более 20-25 увеличивается точность вычисления средних величин, но существенно искажаются особенности варьирования признака и усложняется математическая обработка. При составлении сгруппированного ряда необходимо учесть, что: группы вариант должны располагаться в определенном порядке (в восходящем или нисходящем); интервалы в группах вариант должны быть одинаковыми; значения границ интервалов не должны совпадать, т.к. неясно будет, в какие группы относить отдельные варианты; не рекомендуется оставлять открытых интервалов (50 лет и старше, до 0,6 мг% и т.д.). необходимо учитывать качественные особенности собираемого материала при установлении пределов интервалов (например, при изучении веса взрослых людей интервал 3-4 кг допустим, а для детей первых месяцев жизни он не должен превышать 100 г.) Построим сгруппированный (интервальный) ряд, характеризующий данные о частоте пульса (число ударов в минуту) у 55 студентов-медиков перед экзаменом: 64, 66, 60, 62, 64, 68, 70, 66, 70, 68, 62, 68, 70, 72, 60, 70, 74, 62, 70, 72, 72, 64, 70, 72, 76, 76, 68, 70, 58, 76, 74, 76, 76, 82, 76, 72, 76, 74, 79, 78, 74, 78, 74, 78, 74, 74, 78, 76, 78, 76, 80, 80, 80, 78, 78. Для построения сгруппированного ряда необходимо: Определить величину интервала; Определить середину, начало и конец групп вариант вариационного ряда. ● Величина интервала (i) определяется по числу предполагаемых групп (r), количество которых устанавливается в зависимости от числа наблюдений (n) по специальной таблице (табл. 2). Таблица 2 Число групп в зависимости от числа наблюдений
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
