Учебное пособие управляющего типа Агарков В. И., Бутева Л. В. Грищенко С. В. Донецк Донгму, 2006. 277 с
 Скачать 3.03 Mb.
|
Выборочная совокупность – часть генеральной совокупности, отобранная специальным методом и предназначенная для характеристики генеральной совокупности (см. раздел «Методика организации статистического исследования в здравоохранении»).При проведении выборочного исследования мы можем встретиться с общими ошибками и ошибками выборки. Общие ошибки могут иметь как системный характер (методические ошибки, недостатки измерительной аппаратуры), так и случайный (ошибки исследователя). Ошибки же выборочного исследования связаны с выбором единиц наблюдения. Это ошибки типичности, репрезентативности. Репрезентативность– это соответствие данных выборочной и всей (генеральной) совокупностей. В процессе анализа рассчитанные показатели (средняя длительность лечения, частота осложнений, уровень летальности и другие) рассматривают как обобщающие величины. Если результаты получены на основе достаточного за количеством и качественно однородного материала (требования к выборочной совокупности, являющиеся сущностью понятия репрезентативности), то можно считать, что они достаточно точно характеризуют исследуемые явления. Например, при изучении эффективности нового метода лечения, апробированного на 400 больных, установлено, что у 12 из них возникли осложнения. Частота их, следовательно, составляет 3 случая на 100 больных. Значение обобщающего результата состоит в том, что при проведении аналогичных выборочных исследований или для оценки всей совокупности больных с данной патологией (генеральной совокупности) мы могли бы предусмотреть получение аналогичных данных: 3 случая осложнений на 100 больных. Однако не исключена ситуация, когда при проведении повторных исследований показатель, определяемый путем выборочного наблюдения, в незначительной мере может отличаться от данного результата. Следовательно, оценить достоверность результатов выборочного исследования означает определить, в какой мере сделанные для него выводы (результаты) можно перенести на генеральную совокупность. То есть, на основании части явления рассуждать о явлении в целом и основных присущих ему закономерностях. Достоверность– это степень соответствия полученных показателей отображаемой действительности. Для оценки достоверности результатов каких-нибудь выборочных исследований определяют среднюю ошибку относительной или средней величины (ошибку репрезентативности). Ошибка репрезентативности (m) – это мера достоверности, которая показывает, на сколько отличается величина, полученная при выборочном методе исследования от величин, которые могли бы быть получены при сплошном методе исследований того же явления. Средняя ошибка для соответствующих показателей при значительном числе наблюдений (n>30) может быть рассчитана на основании следующих формул:  – средняя ошибка средней величины; – средняя ошибка относительной величины;где:  – среднеквадратическое отклонение;n – число наблюдений в выборочной совокупности. При малом числе наблюдений (менее 30) вместо n используется (n-1); P – относительный показатель; q – величина, обратная относительному показателю, т. е. вероятность того, что данное явление не будет зарегистрировано. Сумма двух противоположных вероятностей равно единице: P + q= 1. Если показатель рассчитан на 100 (%), то q= 100 – P; если на 1000 (‰), то q= 1000 – Pи т. д. Средняя ошибка относительного (интенсивного) показателя в приведенном выше примере составляет:  (на 100)Ошибка позволяет определить пределы, в которых с соответствующей степенью вероятности безошибочного прогноза находится истинное значение искомого показателя, т.е. доверительные границы. Доверительный интервал (∆) – показатель, с помощью которого с определенной вероятностью безошибочного прогноза (Рт) можно получить границы колебаний средней или относительной величины в генеральной совокупности(доверительные границы). Доверительный интервал ∆=.±tm. И соответственно доверительные границы средней и относительной величин определяют по формулам: Мген.= Мвыб.± ∆ = Мвыб.± t  – для средней величины;Рген.= Рвыб.± ∆ = Рвыб.± t  – для относительной величины; где: Мген. и Рген. – значения средней и относительной величин в генеральной совокупности; Мвыб. и Рвыб. – значения средней и относительной величин, рассчитанных для выборочной совокупности; и – средние ошибки соответствующих показателей;t – критерий достоверности (или вероятности). Вероятность безошибочного прогноза (Рt) – это вероятность, с которой можно утверждать, что в генеральной совокупности средняя или относительная величины будут находиться в пределах Мвыб+tmМ или Рвыб±tmp. Определенной степени вероятности безошибочного прогноза соответствует константное значение критерия «t», величина которого при n>30 определяется по таблице интеграла вероятности (например, при Рt =0,95 → t=2,0; при Рt =0,99 → t=3,0 и т.д.). При n<30 используется краткая таблица критических значений критерия «t» Стьюдента (табл. 1) Таблица 1 Краткая таблица критических значений критерия «t» Стьюдента
В медико-биологических и социально-гигиенических исследованиях минимальной достаточной вероятностью безошибочного прогноза является 95,5% (Pt=0,95), что допускает вероятность ошибки р=0,05. И только в наиболее ответственных случаях, когда необходимо сделать особенно важные в теоретическом или практическом отношении выводы, когда от результатов исследования зависит принятие решения, достаточной вероятностью считается 99,7% (Pt=0,99 или р=0,01). Таким образом, при определенной степени вероятности безошибочного прогноза (а ее задают на этапе планирования статистического исследования) и строго соответствующем ей критерии «t» величина доверительного интервала зависит от величины ошибки репрезентативности, значение которой уменьшается при увеличении числа наблюдений. В приведенном выше примере при применении нового метода лечения частота осложнений для генеральной совокупности с вероятностью 95,5% (t=2) находится в пределах: Рген.= Рвыб.±t =3,0±2*0,85=3,0±1,7 (т.е. от 1,3 сл. на 100 больных до 4,7 сл. на 100 больных);при вероятности же 99,7% (t=3): Рген.= Рвыб.±t =3,0±3*0,85=3,0±2,6 (т.е. от 0,4 сл. на 100 больных до 5,6 сл. на 100 больных).Практическая ценность использования средней ошибки заключается не только в определении доверительных границ для конкретного показателя, а и в оценке его достоверности. Достоверность показателя определяется на основе отношения его абсолютного значения к величине его средней ошибки (  ). Показатель считается достоверным с вероятностью безошибочного прогноза ≥95,5%, если это отношение ≥2; с вероятностью безошибочного прогноза ≥97,7%, если это отношение ≥3. Если отношение абсолютного значения показателя к его средней ошибке составляет менее 2, то в этом случае показатель, рассчитанный для выборочной совокупности, считается недостоверным, т.е. таким, который не может быть использован для каких-либо суждений и выводов о всей генеральной совокупности. В нашем примере:  = =3,5; т. е. полученный в выборочном исследовании показатель частоты осложнений достоверен с вероятностью безошибочного прогноза >97,7%.В медико-биологических исследованиях часто возникают ситуации, когда при сравнении отдельных параметров необходимо оценить значимость различий между ними. Значимая (достоверная) разница между отдельными показателями выборочного исследования свидетельствует о возможности перенесения полученных выводов на генеральную совокупность. 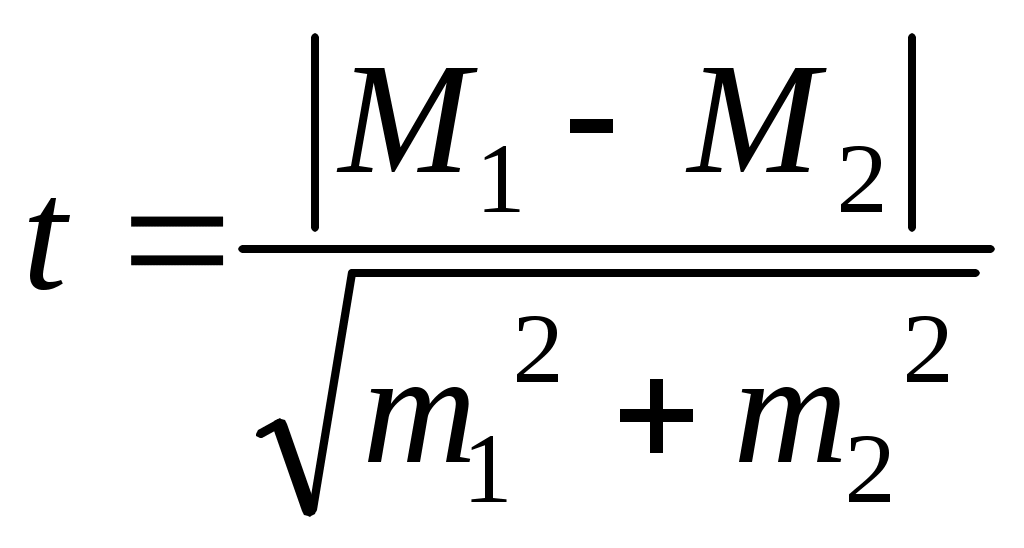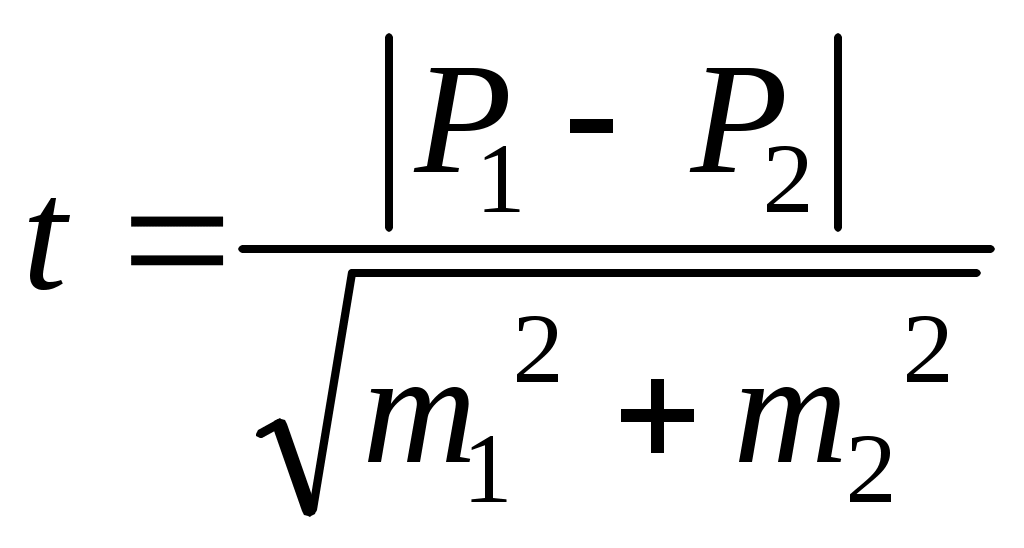Наиболее распространенный метод оценки достоверности разности между сравниваемыми выборочными результатами – метод непрямой разности, в основе которого лежит расчет коэффициента достоверности различий «t» (критерия Стьюдента):  – для средних величин; – для относительных величин.Разница между сравниваемыми выборочными величинами существенна и статистически достоверна с вероятностью безошибочного прогноза ≥95,5%, если величина критерия «t» равна или больше 2 (при n>30). В наиболее ответственных случаях t≥3 (Pt≥0,99, р≤0,01). Например: в школе обучается 1200 детей. Профилактические прививки против гриппа сделаны 900 детям. Заболело гриппом 350 школьников, в том числе 150 учащихся, среди которых не была проведена профилактическая вакцинация. Для оценки эффективности профилактической вакцинации против гриппа необходимо определить достоверность различий между уровнями заболеваемости гриппом среди привитых и непривитых школьников. Для этого следует: 1) определить интенсивные показатели заболеваемости гриппом среди привитых и непривитых детей: Р1=  случаев на 100 детейР2=  случаев на 100 детей2) определить средние ошибки рассчитанных интенсивных показателей: m1=  на 100 m2= на 1003) оценить достоверность различий на основании критерия Стьюдента:  Вывод: различия между показателями заболеваемости гриппом среди привитых и непривитых школьников достоверны с вероятностью безошибочного прогноза >99,7%, так как t >3. Ошибка репрезентативности, доверительные границы, критерий Стьюдента могут быть рассчитаны не только для относительной и средней арифметической величин, но и для любого параметрического критерия, полученного в результате выборочного наблюдения. При этом критерий Стьюдента используется в основном для нормального альтернативного распределения. ЗАДАНИЯ ДЛЯ КОРРЕКЦИИ УМЕНИЙ Для контроля усвоения темы и достижения целей занятия решите следующую задачу. Задача 1 В ЛОР-отделении по поводу паратонзиллярного абсцесса было пролечено 75 больных. Средняя длительность лечения больных составила 17,3 дня; среднее квадратичное отклонение – 9,2 дня. У 12 из 75 больных был использован новый метод лечения. Среди параметров, по которым оценивались результаты лечения, была частота пульса, которая составила в среднем до лечения 81,0±3,2 ударов в минуту, после лечения – 69,0 ударов в минуту (среднеквадратическое отклонение – 8,7 ударов в минуту). Задания: Обоснуйте выбор методики расчета ошибки репрезентативности и рассчитайте ее: для средней длительности лечения больных паратонзиллярным абсцессом; для частоты пульса после лечения. Определите возможность использования приведенных в ситуации средних величин в дальнейших исследованиях (т.е. их достоверность). Вычислите критерий достоверности различий в частоте пульса у больных до и после лечения новым методом. Определите доверительные границы средней длительности лечения больных по поводу паратонзиллярного абсцесса при вероятности безошибочного прогноза: 95,5% (Pt=0,95); 99,7% (Pt=0,99). Сделайте выводы. Ответ: 1. Учитывая, что средняя длительность лечения больных по поводу паратонзиллярного абсцесса была изучена на 75 больных, то есть число наблюдений (n) больше 30 (n>30), необходимо использовать следующую методику расчета ошибки репрезентативности: m1=± дняУчитывая, что средняя частота пульса у больных после лечения измерялось у 12 больных, то есть n<30, необходимо использовать следующую методику расчета ошибки репрезентативности:  m2 уд./ в мин.2. Для определения возможности использования приведенных в ситуации средних величин в дальнейших исследованиях необходимо среднюю величину сравнить с ее ошибкой: для средней длительности лечения больных по поводу паратонзиллярного абсцесса  для средней частоты пульса у больных после лечения  для средней частоты пульса у больных до лечения  Так как все рассчитанные критерии «t» больше 3, следовательно все приведенные в ситуации средние величины достоверны с вероятностью безошибочного прогноза более 99,7%, то есть могут быть использованы в дальнейших исследованиях. 3. Критерий достоверности различий в частоте пульса у больных до и после лечения новым методом определяется следующим образом: 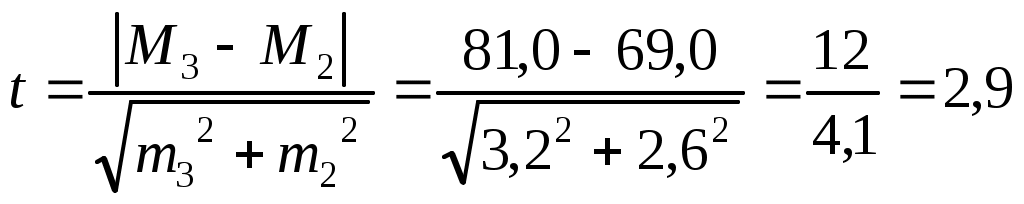 4. Учитывая, что при n>30 и Pt=0,95 критерий t равен 2, а при Pt=0,99 критерий t равен 3, определим доверительные границы показателя средней длительности лечения больных по поводу паратонзиллярного абсцесса в генеральной совокупности с различной вероятностью безошибочного прогноза:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||