Учебное пособие управляющего типа Агарков В. И., Бутева Л. В. Грищенко С. В. Донецк Донгму, 2006. 277 с

• Название: Учебное пособие управляющего типа Агарков В. И., Бутева Л. В. Грищенко С. В. Донецк Донгму, 2006. 277 с
• Дата: 24.03.2023
• Размер: 3.03 Mb.
• Имя файла: Posobie_po_med_statistike.doc
• Тип: Учебное пособие; #1011845
• страница: 15 из 35

2. 
   Построенный вариационный ряд – дискретный или прерывистый, т.к. варианты отличаются друг от друга на целое число и не имеют промежуточных дробных значений.
   
3. 
   Вариационный ряд – простой, т.к. каждая варианта встречается только один раз, т.е. р=1 (графа 2, табл. 2.1).
   
4. 
   Так как вариационный ряд простой, необходимо рассчитать простую среднеарифметическую величину по формуле: ≈168 студентов.
   
5. 
   Моду (Мо) рассчитать нельзя, т.к. р=1.
   
6. 
   Медиана (Ме) рассчитана с учетом центральных вариант. Центральными вариантами являются 4-ая и 5-ая варианты (169 и 171). студентов.
   
7. 
   Lim=175÷ 155 студентов; Am= 175 – 155= 20 студентов. Для расчета среднего квадратического отклонения (δ) определены истинные отклонения (d) вариант от истинной средней арифметической и заполнены графы 3, 4 табл. 2.1 студентов.
   

δ по Ермолаеву = студентов.

С_V= .

Выводы:

1. 
   Вариационный ряд – дискретный, простой.
   
2. 
   На лекциях по социальной медицине в весеннем семестре присутствовало в среднем 168 студентов IV курса лечебного факультета.
   
3. 
   Средняя арифметическая величина является характерной, типичной для данного вариационного ряда, т.к. в пределах 153,2 – 182,8 (М±2δ) находятся все варианты вариационного ряда, а достаточно 95%.
   
4. 
   Степень колеблемости вариационного ряда малая по коэффициенту вариации.
   

Задача 3

Сроки стационарного лечения 30 больных детей (в днях): 17, 7, 16, 18, 12, 12, 14, 14, 17, 18, 15, 18, 19, 17, 15, 15, 15, 17, 16, 9, 10, 10, 11, 16, 19, 20, 16, 17, 15, 15.
Задания.

1. 
   Постройте вариационный ряд и определите его вид (ответ обоснуйте).
   
2. 
   Рассчитайте среднюю арифметическую величину, моду, медиану.
   
3. 
   Определите показатели колеблемости вариационного ряда (лимит, амплитуду, среднее квадратическое отклонение, коэффициент вариации).
   
4. 
   Оцените полученные данные и сделайте выводы.
   

Ответ.

1. 
   Для построения вариационного ряда варианты были расположены в возрастающем порядке (графа 1, табл. 3.1).
   

Таблица 3.1

Распределение больных детей по срокам

стационарного лечения

Сроки стационарного лечения (в днях), V	Число больных р	Vр	d	d2	d2р
1	2	3	4	5	6
7 9 10 11 12 14 15 16 17 18 19 20	1 1 2 1 2 3 6 4 4 3 2 1	7 9 20 11 24 42 90 64 68 54 38 20	-8 -6 -5 -4 -3 -1 0 +1 +2 +3 +4 +5	64 36 25 16 9 1 0 1 4 9 16 25	64 36 50 16 18 3 0 4 16 27 32 25
	Σр=n=30	ΣVр=447			Σd2p=291

2. 
   Построенный вариационный ряд – дискретный или прерывистый, т.к. варианты отличаются друг от друга на целое число и не имеют промежуточных, дробных значений. Вариационный ряд – взвешенный, т.к. одна и та же варианта повторяется несколько раз, варианты как бы взвешиваются по числу соответствующих им частот – р>1 (графа 2, табл. 3.1).
   
3. 
   Учитывая, что вариационный ряд взвешенный, была рассчитана взвешенная среднеарифметическая величина по формуле: дней.
   
4. 
   Мода (Мо) – рассчитывалась как наиболее часто встречающаяся варианта, чаще всего (6 раз) встречались дети со сроком стационарного лечения 15 дней. Следовательно, Мо=15 дней.
   

5. 
   Число наблюдений в данной задаче четное, поэтому медиана (Ме) рассчитывалась следующим образом: 30 : 2 = 15, т.е. медиана соответствует 15-й по счету варианте, это варианта – 15 дней. Следовательно, Ме=15 дней.
   
6. 
   Lim=20÷7; Am=13. Для расчета среднего квадратического отклонения определялись истинные отклонения вариант от истинной среднеарифметической величины (d) и заполнялись графы 4, 5, 6 табл. 3.1).
   

дней.

δ по Ермолаеву = дней.

С_V= .

7. 
   Выводы.
   

• 
  Вариационный ряд – дискретный, взвешенный.
  
• 
  Мо=Ме≈М, что характерно для нормального распределения.
  
• 
  Сроки стационарного лечения больных детей составляет в среднем 14,9≈15 дней.
  
• 
  Средняя арифметическая величина является типичной для данного вариационного ряда, т.к. в пределах М±2δ находится около 97% вариант вариационного ряда.
  
• 
  Степень колеблемости вариационного ряда сильная по коэффициенту вариации, вместе с тем мы не можем говорить о ненадежности средней арифметической, т.к. С_V<40%.
  

Задача 4

Число состоящих на диспансерном учете больных с гипертонической болезнью у 50 участковых терапевтов города: 20, 21, 22, 23, 25, 25, 26, 27, 27, 25, 26, 27, 25, 22, 23, 24, 39, 23, 40, 22, 26, 30, 24, 26, 24, 25, 24, 25, 24, 28, 24, 29, 25, 26, 27, 27, 30, 31, 34, 31, 35, 32, 30, 30, 36, 25, 35, 38, 39, 28.

Задания.

1. 
   Постройте вариационный ряд и определите его вид (ответ обоснуйте).
   
2. 
   Рассчитайте среднюю арифметическую величину, моду, медиану.
   
3. 
   Определите показатели колеблемости вариационного ряда (лимит, амплитуду, среднее квадратическое отклонение, коэффициент вариации).
   
4. 
   Оцените полученные данные и сделайте выводы.
   

Ответ.

1. 
   Чтобы построить вариационный ряд, расположим варианты в возрастающем порядке (графа 1, табл. 4.1).
   

2. Построенный первоначальный ряд – дискретный, т.к. варианты отличаются друг от друга на целое число и взвешенный, т.к. варианты повторяются несколько раз (графа 2, табл. 4.1). Учитывая, что число наблюдений равно 50 (n>30), и для облегчения расчетов из первоначального ряда построим сгруппированный вариационный ряд с соответствующими частотами (графы 3, 4, табл. 4.1). Величина интервала (i) для сгруппированного ряда рассчитывалась по формуле: , где r – число предполагаемых групп (см. табл. 2). ≈ 2 больных.
Таблица 4.1

Распределение больных гипертонической болезнью,

состоящих на диспансерном учете у участковых терапевтов

Первоначальный ряд		Сгруппированный ряд
Число больных, состоящих на диспанс. учете, V	Число участковых терапевтов, р	Число больных, состоящих на диспан. учете, V	Число участковых терапевтов, р	V	р	а	ар	а2р
1	2	3	4	5	6	7	8	9
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40	1 1 3 3 6 8 5 5 2 1 4 2 1 0 1 2 1 0 1 2 1	20 – 21 22 – 23 24 – 25 26 – 27 28 – 29 30 – 31 32 – 33 34 – 35 36 – 37 38 – 39 40 – 41	2 6 14 10 3 6 1 3 1 3 1	21 23 25 27 29 31 33 35 37 39 41	2 6 14 10 3 6 1 3 1 3 1	-2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8	4 6 0 10 6 18 4 15 6 21 8	8 6 0 10 12 54 16 75 36 147 64
	∑р=n=50		∑р=n=50		n=50		∑ар=98	∑а2р=428

Так как вариационный ряд взвешенный, рассчитываем взвешенную среднюю арифметическую с использование способа моментов, т.к. число наблюдений n>30.

больных.

Величина интервала (i) вводится в формулу определения М и δ в том случае, если в графе 7 «условные отклонения» – а определяются не как разность между вариантами и условными средними (V – А), а даются условные обозначения –1, -2, 0, +1, +2 и т.д., предполагающие, что разность между центральными вариантами равна 1. Мо=25 больных; Ме=26 больных.

3. 
   Lim=40 ÷ 20; Am=20.
   

δ по Ермолаеву = больных.

С_V= .

Выводы.

1. 
   Вариационный ряд – дискретный, взвешенный, сгруппированный.
   
2. 
   Мо=25 больных; Ме=26 больных.
   
3. 
   Lim=40 ÷ 20; Am=20.
   
4. 
   У участковых терапевтов на диспансерном учете состоит в среднем 28,9≈29 больных.
   
5. 
   Средняя арифметическая величина является типичной для данного вариационного ряда, т.к. в пределах М±2δ (20,5 ÷ 37,7) находится 95% вариант вариационного ряда.
   
6. 
   Степень колеблемости вариационного ряда средняя (по коэффициенту вариации).
   

Задача 5

Результаты измерения роста у мальчиков 10 лет, обучающихся в школах-интернатах (в см): 127,0; 126,5; 128,0; 120,0; 123,0; 121,0; 126,0; 123,5; 122,0; 127,0; 123,0; 122,5; 127,0; 126,0; 128,5; 124,5; 127,0; 125,5; 125,5; 128,0; 125,0; 127,0; 130,0; 123,5 128,0; 126,0; 124,5; 127,0; 123,5; 127,0; 130,0; 126,5; 126,0; 128,0; 124,5; 127,0; 125,0; 124,5; 128,0; 128,5; 125,5; 128,0; 127,0; 126,0; 126,5; 131,0; 127,0; 127,0; 131,0; 126,0; 128,0; 124,5; 125,0; 127,0; 130,5; 125,0; 127,0; 124,5; 126,0; 128,5 125,0; 128,0; 126,5; 130,0; 125,5; 128,5, 126,0; 126,0; 130,5; 124,5; 128,0; 125,5; 125,0; 128,0; 125,5; 126,0; 124,0; 131,0; 125,5; 130,5; 129,5; 127,0; 128,5 126,5; 130,0; 130,0; 127,0; 127,0; 127,0; 127,0; 128,0; 128,0; 129,0; 129,0; 129,0; 134,5; 130,5; 132,0; 132,0; 133.

Задания.

1. 
   Постройте вариационный ряд и определите его вид (ответ обоснуйте).
   
2. 
   Рассчитайте среднюю арифметическую величину, моду, медиану.
   
3. 
   Определите показатели колеблемости вариационного ряда (лимит, амплитуду, среднее квадратическое отклонение, коэффициент вариации).
   
4. 
   Оцените полученные данные и сделайте выводы.
   

Ответ.

1. 
   Чтобы построить вариационный ряд, расположим варианты в возрастающем порядке (графа 1, табл. 5.1).
   
2. 
   Построенный первоначальный ряд – непрерывный, т.к. варианты имеют промежуточные, дробные значения, и взвешенный, т.к. одна и та же варианта встречается несколько раз (графа 2, табл. 5.1). Так как число наблюдений большое (n=100), для облегчения расчетов из первоначального ряда построим сгруппированный вариационный ряд с соответствующими группам частотами (графы 3, 4, табл. 5.1).
   

Таблица 5.1

Распределение мальчиков по росту (в см)

Первоначальный ряд		Сгруппированный ряд
Рост, V	Число мальчиков, р	Рост, V	Число мальчиков, р	V	р	а	ар	а2р
1	2	3	4	5	6	7	8	9
120,0 121,0 122,0 122,5 123,0 123,5 124,5 125,0 125,5 126,0 126,5 127,0 128,0 128,5 129,0 129,5 130,0 130,5 131,0 132,0 133,0 134,5	1 1 1 1 2 3 8 6 7 10 5 18 12 5 3 1 5 4 3 2 1 1	120,0 – 121,9 122,0 – 123,9 124,0 – 125,9 126,0 – 127,9 128,0 – 129,9 130,0 – 131,9 132,0 – 133,9 134,0 – 135,9	2 7 21 33 21 12 3 1	121,0 123,0 125,0 127,0 129,0 131,0 133,0 135,0	2 7 21 33 21 12 3 1	-6 -4 -2 0 +2 +4 +6 +8	-12 -28 -42 0 +42 +48 +18 +8	72 112 84 0 84 192 108 64
	∑р=n =100		∑р=n =100		n=100		∑ар =34	∑а2р =716

3. 
   Величина интервала (i) для сгруппированного ряда рассчитывалась по формуле: , где r – число предполагаемых групп (см. табл. 2).
   

≈ 2 см

Так как вариационный ряд взвешенный, рассчитываем взвешенную среднюю арифметическую. Учитывая, что число наблюдений большое, используем способ моментов:

см

Величина интервала (i) не введена в формулы определения М и δ, т.к. условное отклонение – а определялось как разность (V – А), где А – условная средняя, наиболее часто встречающаяся варианта.

4. 
   Lim=134,5 ÷ 120,0: Am=14,5.
   

см

δ по Ермолаеву = см.

С_V= .

Выводы.

1. 
   Вариационный ряд – непрерывный, взвешенный, сгруппированный.
   
2. 
   Мо=Ме=М, что характерно для нормального распределения.
   
3. 
   Lim=134,5 ÷ 120,0; Am=14,5.
   
4. 
   Средний рост мальчиков 10 лет, обучающихся в школах-интернатах, составляет 127,3 см.
   
5. 
   Средняя арифметическая величина является типичной для данного вариационного ряда, т.к. в пределах 116,5 – 138,1 см (М±2δ) находятся все варианты вариационного ряда.
   
6. 
   Степень колеблемости ряда слабая (С_V<10%).
   

Приложение 1

Граф логической структуры темы: «Средние величины, их использование в здравоохранении»


ПОНЯТИЕ О ВАРИАЦИОННОМ РЯДЕ, ЕГО РАЗНОВИДНОСТИ



ВИДЫ ВАРИАЦИОННЫХ РЯДОВ



По характеру количественного признака

По частоте встречаемости вариант



прерывные

взвешенные

простые

непрерывные



МЕТОДИКА СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ВАРИАЦИОННЫХ РЯДОВ



расчет средних величин

оценка достоверности

расчет показателей колеблемости

Ι ΙΙ


Виды средних величин

Критерии колеблемости признака, характеризующие



параметрические

непараметрические

границы совокупности

внутреннюю структуру совокупности





средняя арифметическая

средняя прогрессивная

мода

коэффициент вариации

среднее квадратическое отклонение

амплитуда

лимит

медиана






Виды средней арифметической величины





вычисленная по способу моментов


простая

взвешенная





методика расчета параметрических и непараметрических средних

методика расчета критериев колеблемости изучаемого признака



Практическое применение средних величин и критериев колеблемости изучаемого признака



Приложение 2

Логическая структура темы: «Средние величины, их использование в здравоохранении»

(фрагмент темы: «Расчет средних величин»)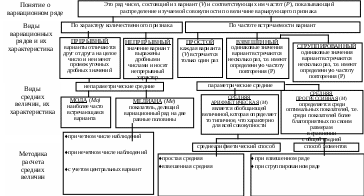




Приложение 3

Логическая структура темы "Средние величины, их использование в здравоохранении"

(фрагмент темы "Расчет показателей колеблемости вариационного ряда")


Критерии колеблемости признака характеризующие


Критерии

колеблемости

изучаемого

признака,

их характеристика





границы совокупности

внутреннюю структуру совокупности





ЛИМИТЫ (Lim)

пределы – минимальная и максимальная варианты изучаемой совокупности

СРЕДНЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ(δ)

мера колеблемости вариационного ряда (изучаемого признака;

применяется в случаях, если сравниваются только однородные (одноименные) совокупности или средние уровни, сравниваемых признаков, значительно отличаются друг от друга;

является критерием надежности, типичности средней арифметической величины.




АМПЛИТУДА (Am)

размах вариации – разность лимитов (крайних вариант)

КОЭФФИЦИЕНТ

ВАРИАЦИИ (С_V)

мера колеблемости вариационного ряда (изучаемого признака;

применяется в случае, если сравниваются неоднородные совокупности;

является критерием надежности средней арифметической величины.




Vmax ÷ Vmin

Vmax – Vmin


Методика

расчета критериев

колеблемости

признака




СРЕДНЕАРИФМЕТИЧЕСКИЙ СПОСОБ

при n≤30 и p=1:



при n≤30 и p>1:



при n>30 в знаменателе обеих формул берут n, а не n–1.









ПО АМПЛИТУДЕ РЯДА





Приложение 4

Алгоритм статистической обработки медицинских данных с помощью средних величин



Приложение 5

Алгоритм расчета параметров взвешенного вариационного ряда

	Построить взвешенный вариационный ряд, расположив все варианты (V) в возрастающем или убывающем порядке с соответствующими им частотами (р), графа 1 и 2.
	Перемножить каждую варианту на соответствующую частоту (Vр), найти их сумму (∑Vр), графа 3.
	Рассчитать среднюю арифметическую взвешенную (М).
	Найти истинные отклонения d = V – M, графа 4.
	Возвести каждое истинное отклонение в квадрат d2, графа 5.
	Найти произведение d2×р, по всем строкам ряда и определить их сумму ∑d2×р, графа 6.
	Рассчитать среднее квадратическое отклонение (δ).
	Определить ошибку репрезентативности (m).*
	Рассчитать критерий достоверности (t).*

V	р	Vp	d (V–M)	d2	d2p	Формулы для расчета
1	2	3	4	5	6	7
						* *
	∑р=n	∑Vp			∑d2p

Примечание. * ошибка репрезентативности (m) и критерий достоверности (t) будут рассмотрены в следующей теме.

Приложение 6

Алгоритм расчета параметров взвешенного ряда по способу моментов

	Построить взвешенный вариационный ряд, расположив все варианты (V) в возрастающем или убывающем порядке с соответствующими им частотами (р), графа 1 и 2.
	Выбрать условную среднюю (А) – можно взять любую варианту ряда, но желательно наиболее часто встречающуюся варианту.
	Определить условное отклонение (а) каждой варианты от условной средней (а = V – А), графа 3.
	Перемножить значение каждого условного отклонения на соответствующую частоту (aр), найти их сумму (∑aр), графа 4.
	Найти истинную среднюю арифметическую взвешенную по способу моментов (М), формула 1.
	Возвести каждое условное отклонение (а) в квадрат (а2), найти произведение (а2р) по всем строкам ряда и определить их сумму ∑a2р, графа 5, 6.
	Рассчитать среднее квадратическое отклонение (δ) по способу моментов, формула 2.
	Определить ошибку репрезентативности (m)*, формула 3.
	Рассчитать критерий достоверности (t)*, формула 4.

V	р	A (V-A)	ap	a2	a2p	Формулы для расчета
1	2	3	4	5	6	7
						(1) (2) * (3) * (4)
	∑р=n	∑ар			∑a2p

Примечание. * ошибка репрезентативности (m) и критерий достоверности (t) будут рассмотрены в следующей теме.

Приложение 7

Алгоритм расчета параметров сгруппированного ряда по способу моментов

	Построить сгруппированный вариационный ряд, определив число групповых вариант (не менее 5), величину интервала (i) по специальной таблице, середину, начало и конец групп вариант. Расположить группы вариант в возрастающем или убывающем порядке с соответствующими им частотами (р), графа 1 и 3.
	Определить центральную варианту V (в непрерывных вариационных рядах как полусумму первых значений соседних групп, в дискретных вариационных рядах как полусумму крайних значений группы), графа 2
	Принять за единицу разность между соседними вариантами, введя в формулу для расчета средней арифметической величину интервала (i).
	Выбрать условную среднюю А – можно взять любую варианту ряда, но желательно наиболее часто встречающуюся варианту.
	Определить условное отклонение (а) каждой варианты от условной средней (а = V – А), графа 4.
	Перемножить значение каждого условного отклонения (а) на соответствующую частоту (ар) и определить их сумму ∑aр, графа 5.
	Найти истинную среднюю арифметическую взвешенную сгруппированного ряда по способу моментов (М), формула 1.
	Возвести каждое условное отклонение (а) в квадрат (а2), найти произведение (а2р) по всем строкам ряда и определить их сумму ∑a2р, графа 6, 7.
	Рассчитать среднее квадратическое отклонение (δ) по способу моментов, формула 2.
	Определить ошибку репрезентативности (m)*, формула 3.
	Рассчитать критерий достоверности (t)*, формула 4.

V	р	A (V-A)	ap	a2	a2p	Формулы для расчета
1	2	3	4	5	6	7
						(1) (2) * (3) * (4)
	∑р=n	∑ар			∑a2p

Примечание. * ошибка репрезентативности (m) и критерий достоверности (t) будут рассмотрены в следующей теме.

ТЕМА 4. МЕТОДИКА ОЦЕНКИ ДОСТОВЕРНОСТИ

ОТНОСИТЕЛЬНЫХ И СРЕДНИХ ВЕЛИЧИН
Актуальность темы. При проведении различных медико-биологических исследований в практической или научной деятельности врача преимущественно пользуются выборочным методом сбора информации.

Выборочный метод выгодный в экономическом отношении, так как может быть проведен при меньшем количестве персонала и с меньшими материальными затратами, но при проведении выборочных исследований необходимо обеспечить представительность (репрезентативность) выборочной совокупности. В этом случае к выборочной совокупности предъявляют два основных требования:

• 
  она должна обладать основными характерными чертами генеральной совокупности, то есть быть максимально на нее похожей;
  
• 
  она должна быть достаточной по объему (числу наблюдений), чтобы более точно выразить особенности генеральной совокупности.
  

И, все-таки, какой бы репрезентативной не была выборочная совокупность, она отличается от генеральной потому, что в процессе выборки допускаются случайные ошибки – ошибки выборки, которые показывают, на сколько отличаются величины, полученные при выборочном методе исследования, от величин, которые могли бы быть получены при изучении генеральной совокупности.

Для того, чтобы исследователь имел право перенести выводы, сделанные на результатах выборочной совокупности, на всю генеральную совокупность, определяются показатели достоверности. Использование статистически недостоверных данных может привести к неправильным выводам. Вот почему умение определять показатели достоверности и использовать их для обобщенной количественной характеристики и оценки различных явлений и процессов – весьма важное умение студента и врача.

Учитывая изложенное, перед студентами поставлены следующие цели:


ЦЕЛИ ЗАНЯТИЯ

Общая цель: Уметь оценить достоверность относительных и средних показателей, применяемых для характеристики состояния здоровья населения и деятельности медицинских учреждений.

Общая цель достигается через конкретные умения:

• 
  Рассчитать ошибку репрезентативности относительных и средних показателей.
  
• 
  Вычислить критерий достоверности относительной и средней величины, критерий достоверности разности двух показателей.
  
• 
  Определить доверительные границы в генеральной совокупности.
  
• 
  Оценить достоверность полученных данных и сделать выводы.
  

ИСТОЧНИКИ УЧЕБНОЙ ИНФОРМАЦИИ

(рекомендуемая литература)

1. 
   Соціальна медицина та організація охорони здоров’я/ Під ред. Вороненка Ю.В., Москаленка В.Ф. – Тернопіль: Укрмедкнига, 2000. – С. 62-66.
   
2. 
   Социальная гигиена и организация здравоохранения / Под ред. Серенко А.Ф., Ермакова В.В. – М.: Медицина, 1984. – С. 139-146.
   
3. 
   Руководство по социальной гигиене и организации здравоохранения / Под ред. Лисицына Ю.П. – М.: Медицина, 1987. – Т.1. – С. 228-230.
   
4. 
   Граф логической структуры содержания темы (приложение 1).
   

ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ ТЕМЫ

1. 
   Понятие о выборочной совокупности, репрезентативности.
   
2. 
   Понятие о достоверности.
   
3. 
   Показатели, используемые для оценки достоверности относительных и средних величин: ошибка репрезентативности, критерий достоверности, доверительные границы. Их характеристика.
   
4. 
   Методика расчета ошибки репрезентативности, критерия достоверности статистической величины, критерия достоверности разности показателей; доверительных границ в генеральной совокупности.
   
5. 
   Оценка достоверности полученных результатов.
   

Основные вопросы и ключевые понятия,

на которые следует обратить внимание

при подготовке темы
В системе медико-биологических исследований (кроме данных официальной статистики) редко используются сплошные методы сбора информации – основная часть исследований относится к выборочным.