построение теоретического чертежа корпуса судна. Г. Текст. Волжская государственная академия водного транспорта
 Скачать 3.07 Mb. Скачать 3.07 Mb.
|
|
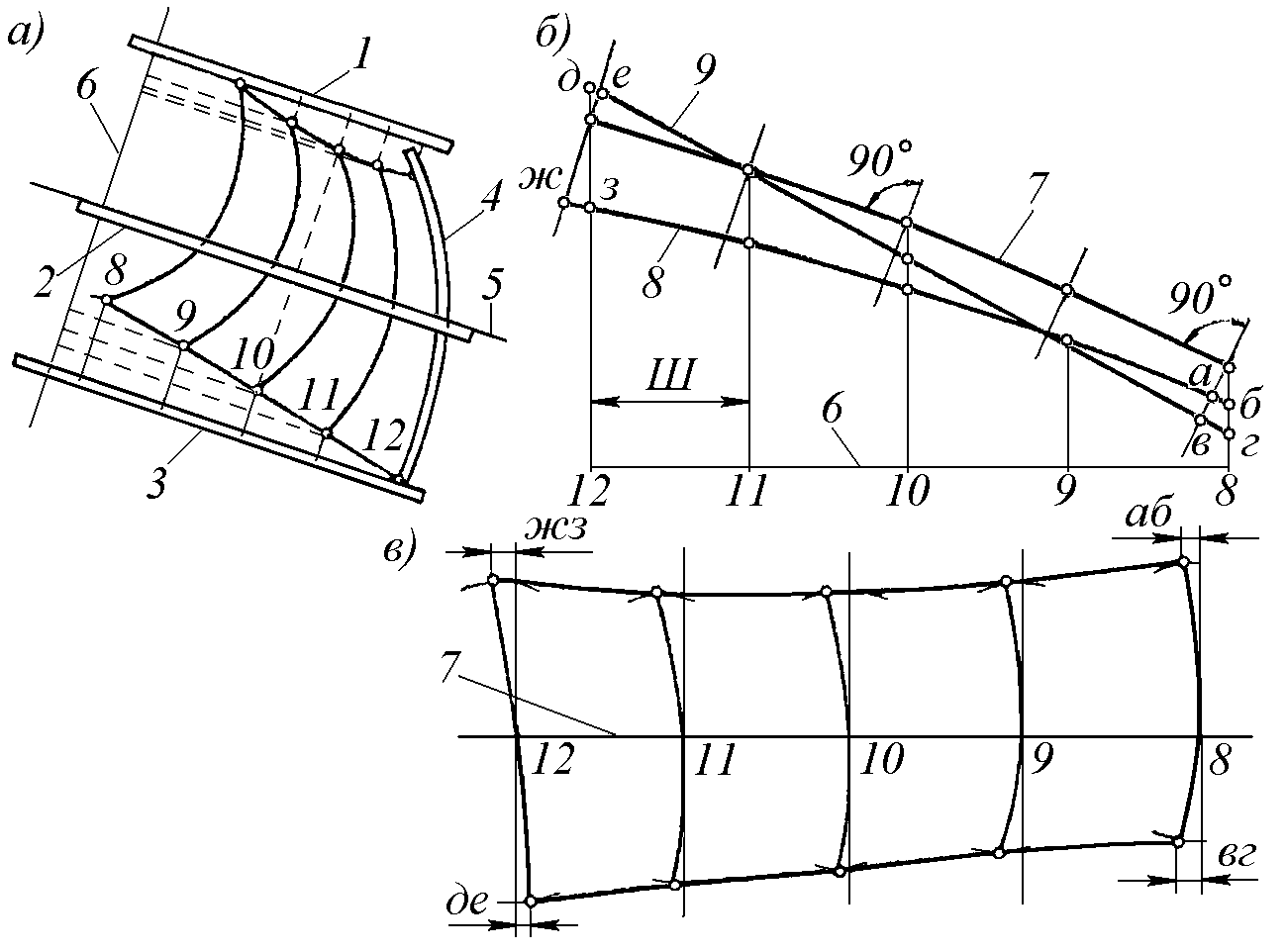
2.4.2. Для определения дополнительных данных, фиксирующих контур развёртываемого листа, существует более 50 различных способов, отличающихся большей или меньшей точностью и обоснованностью геометрических построений. Все графические способы развёртки листов в зависимости от типа вспомогательных построений, используемых при развёртке, можно разделить на две основные группы: 1) развёртки листов при помощи линий, идущих вдоль листа и пересекающих все его шпангоуты, то есть при помощи строевых; 2) развёртки листов при помощи диагональных линий. На отечественных заводах наибольшее распространение нашли из первой группы – способы Е. Е. Егорова и А. М. Челнокова, а из второй – диагональный (голландский) способ. 2.4.3. Развёртывание листа относительно строевой линии, проведённой на проекции «корпус», выполняют по определённому закону. Наиболее приемлемым законом является тот, который обеспечивает получение строевой линии на развёртке листа в виде прямой. Для повышения точности развёртки некоторые методы предусматривают построение нескольких строевых. 2.4.4. Метод Егорова. Метод, предложенный мастером Е. Е. Егоровым, сравнительно прост, но применим для развёртки листов с малой продольной и поперечной погибью и малыми перекосами, то есть с погибью, близкой к цилиндрической или конической поверхностям; в других же случаях применение этого метода даёт заметные отклонения от действительного контура развёрнутого листа и его следует применять осмотрительно. При развертке по методу Егорова строевую вычерчивают в виде прямой и на проекции листа и на его развёртке (рис. 2.13); все остальные линии листа будут менять свой вид и свое положение по мере развёртывания. На проекции листа выбирают средний шпангоут, проводят его хорду и из середины хорды восстанавливают перпендикуляр, который является строевой линией и пересекает (в пределах листа) всю группу шпангоутов. Эта прямая на корпусе одновременно является следом плоскости строевой, перпендикулярной к плоскостям шпангоутов и к хорде среднего шпангоута. За пределами проекции листа, близко к его стыку, обращенному к ДП, строят начальную линию, перпендикулярную к строевой. После этого проецируют на плоскость строевой оба паза и строевую линию, для чего на рейки 1, 2 и 3 снимают ординаты пазов и строевой от начальной линии (рис. 2.13, а).
Пробивая начальную линию и откладывая от неё на соответствующих шпангоутах снятые ординаты, получают проекцию обоих пазов и строевой на плоскость строевой (рис. 2.13, б), причём строевая в этом случае проецируется своей истинной длиной. Отдельно пробивают прямую, на которой откладывают точки пересечения шпангоутов с растянутой строевой и восстанавливают к ним перпендикуляры (рис. 2.13, в). На перпендикулярах по обе стороны от строевой откладывают соответствующие ширины листов по шпангоутам, снятые на рейку 4 с плазового корпуса. Отмеченные точки соединяют плавными кривыми и получают верхнюю и нижнюю пазовые кромки. Однако наличие на развёртке шпангоутных линий, изображённых в виде прямых отрезков, противоречит действительности; необходимо найти их искривление. Вместо стрелки погиби у при работе по методу Егорова учитывают сдвиг концевых точек шпангоутов. Для этого из точек пересечения шпангоутов со строевой (рис. 2.13, в) проводят нормали к строевой, которые пересекут обе пазовые линии. Отрезки аб для верхнего паза и вг для нижнего паза и будут теми сдвигами, которые получат на развёртке листа концы шпангоутов. Эти отрезки на развёртке следует откладывать в те же стороны, в какие берутся их размеры от шпангоутных сечений. 2.4.5. Метод А. М. Челнокова менее условен, более точен, технически обоснован и хорошо подходит для натурного плаза. При развёртке листов по методу А. М. Челнокова в качестве строевой используется так называемая средняя нормаль. Средняя нормаль – это кривая линия, пересекающая шпангоутные линии под прямыми углами к их касательным.
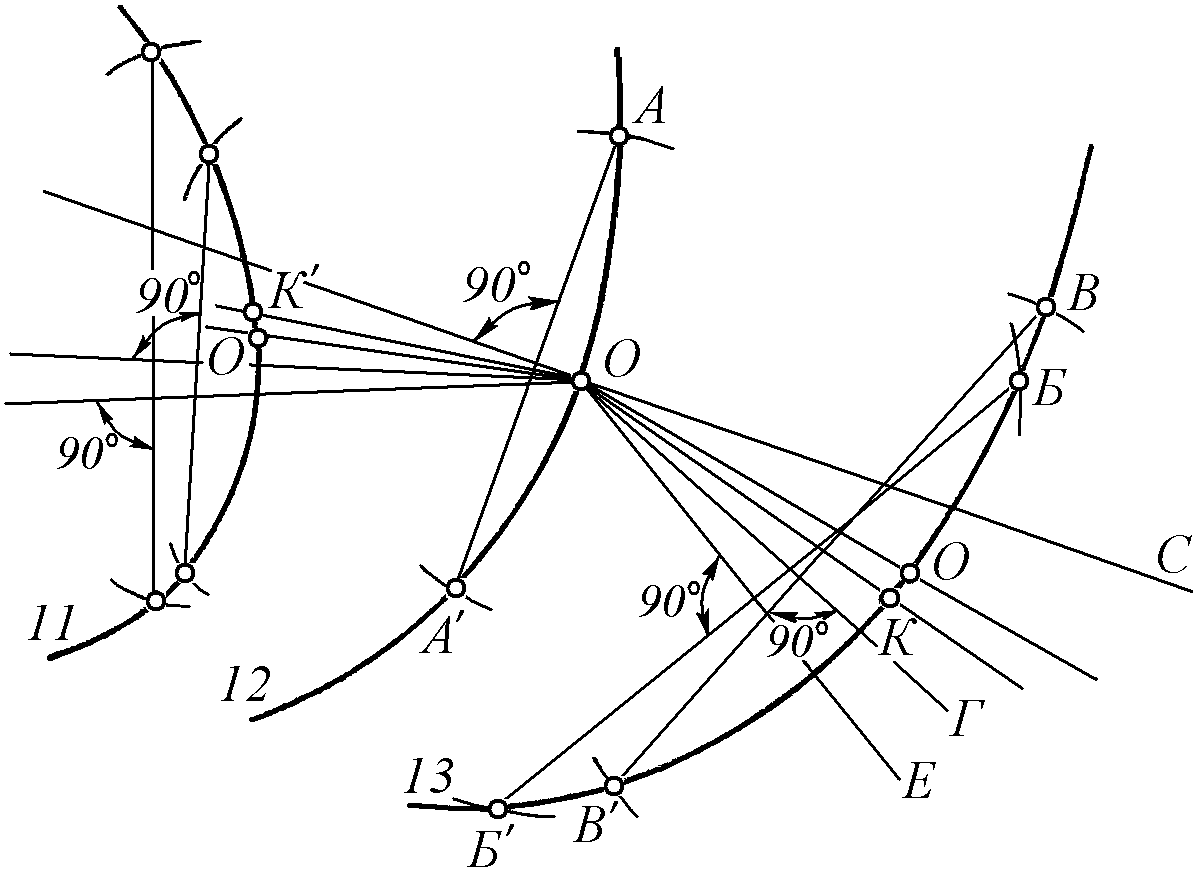
Графическое построение точек средней нормали на шпангоутах плазового корпуса выполняют следующим образом (рис. 2.14). Например, необходимо построить среднюю нормаль к шпангоутным кривым 11, 12, 13, начиная от точки О среднего шпангоута. Из точки О как из центра произвольным радиусом ОА засекают на линии шпангоута точки А и А'. Из точки О восстанавливают перпендикуляр ОС к хорде АА'. Затем из точки О произвольным радиусом ОБ делают засечки на линии соседнего шпангоута 13 в точках Б и Б'. Опускают перпендикуляр из точки О на хорду ББ' и полученный угол СОЕ делят пополам. Биссектриса этого угла пересечет шпангоут 13 в точке К, являющейся в первом приближении точкой средней нормали. При резко изменяющейся кривизне шпангоута касательная к кривой этого шпангоута в точке К иногда не будет параллельна хорде ББ'. Тогда перпендикуляр ОК не будет нормалью к этой кривой в точке К.
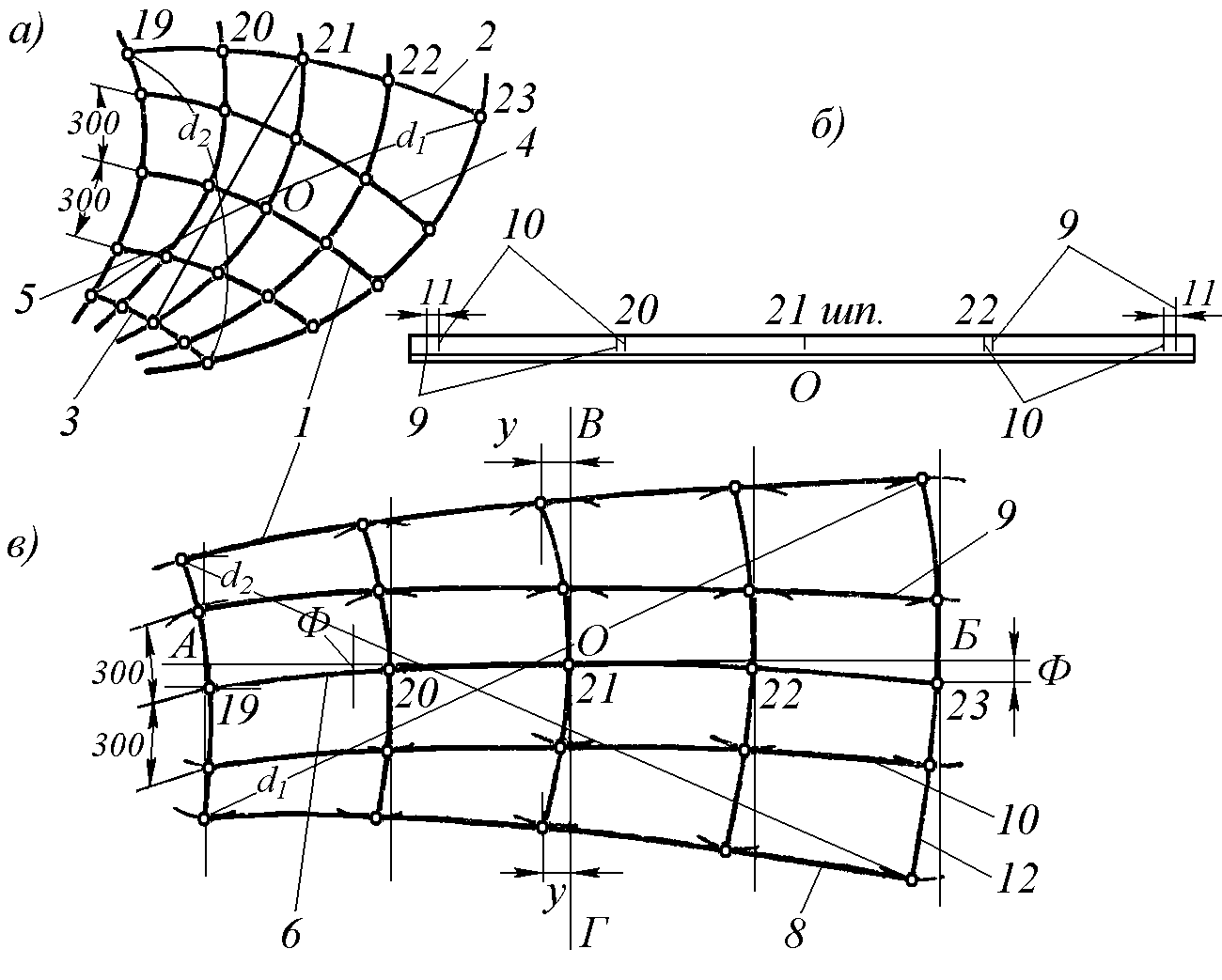
В таких случаях, приняв точку К за середину дуги, от неё в обе стороны шпангоута отмечают равные отрезки KB и KB'. На хорду ВВ' из точки О опускают перпендикуляр ОГ. Проводя биссектрису угла СОГ, на линии шпангоута 13 получают точку О', которая и будет искомой точкой средней нормали для 12-го и 13-го шпангоутов. Точка О', в свою очередь, будет исходной для построения пересечения средней нормали со следующим шпангоутом. Аналогичное построение ведется и в сторону 11 шпангоута. Полученные точки О, О' и О" соединяют плавной кривой, которая будет проекцией средней нормали листа на плазовом корпусе. Построение развёртки листа производят в следующей последовательности. На проекции разворачиваемого листа строят среднюю нормаль, начиная от среднего шпангоута. От неё вверх и вниз на расстоянии 300 мм по обводу шпангоутной линии строят дополнительные вспомогательные строевые – верхнюю и нижнюю (рис. 2.15, а). Для всех пяти продольных линий – верхнего и нижнего пазов, средней нормали и вспомогательных строевых – определяют растяжки, которые снимают на рейку; при этом растяжки пазов и средней нормали снимают на от дельные грани рейки, а растяжки вспомогательных строевых – на одну грань рейки и начиная от среднего шпангоута (шп. 21) к концевым. Так как на рейке риска среднего шпангоута для вспомогательных строевых совмещена, то на ней будут видны разности их растяжек по каждому шпангоуту (рис. 2.15, б), необходимые для определения положения средней нормали на «развернутом листе. Кроме того, изготовляют рейки-растяжки шпангоутов, на которых отмечают риски средней нормали, пазов и вспомогательных строевых. На плазе пробивают прямую АБ (рис. 2.15, б) и перпендикулярно к ней – прямую ВГ. Точка пересечения этих двух прямых является первой точкой средней нормали-строевой. Затем вычерчивают кривую среднего шпангоута, для чего по формуле Стрелку погиби откладывают перпендикулярно к линии ВГ на высоте, равной растяжке среднего шпангоута. Затем по линии АБ укладывают рейку растяжки средней нормали и отмечают ориентировочно (по шпангоутным рискам на рейке растяжки) участки, через которые пройдут шпангоутные кривые. На развёрнутом листе средняя нормаль не будет горизонтальной прямой, а точки пересечения её со шпангоутами расположатся на кривой, которая может иметь выпуклость вверх или вниз от горизонтали в зависимости от направления веерообразности листа. Величины опускания средней нормали от горизонтали на каждом шпангоуте находятся следующим образом. Как уже указывалось, растяжки верхней и нижней вспомогательных строевых снимают на одну сторону рейки, причём риски среднего шпангоута совмещают. Следовательно, для каждого шпангоута непосредственно на рейке будут видны разности растяжек, которые обозначают буквой п. Поэтому составляют таблицу, в которую вносят все данные, необходимые для определения величины опускания средней нормали, обозначаемой буквой Ф. Опускание средней нормали в данной шпации определяют по формуле:
Величины опускания средней нормали откладывают в ту сторону, где растяжка вспомогательной строевой короче. На разворачиваемом листе перпендикулярно к линии АБ против соответствующих шпангоутов откладывают величины опускания и проводят короткие отрезки прямых (длиной 100–150 мм) параллельно линии АБ (рис. 2.15, в). Затем рейку растяжки средней нормали накладывают на лист так, чтобы на прямой АБ и на рейке точки среднего шпангоута совпали; после этого, изгибая рейку, придают ей такое положение, при котором отметка каждого шпангоута ложится на соответствующий ему короткий отрезок прямой, определяющий опускание средней нормали. Линию прочерчивают по рейке. Далее из точек шпангоутов на линии средней нормали, как из центров, радиусом 300 мм вверх и вниз от нормали очерчивают короткие дуги. По этим дугам устанавливают рейки растяжек верхней и нижней вспомогательных строевых линий, причём риску среднего шпангоута на рейке совмещают с соответствующей точкой среднего шпангоута по развёртке листа. На дугах отмечают по рейке точки соответствующих шпангоутов. Таким же образом находят точки пазов, очерчивая дуги радиусами, равными ширине участка от вспомогательной строевой линии до кромки паза при соответствующих шпангоутах. По полученным пяти точкам строят шпангоутные кривые, чем и заканчивается построение развёртки листа. Для проверки правильности выполненных построений пользуются диагоналями. На развёрнутом листе пробивают прямые диагонали (рис. 2.15, в). Точки пересечения их со шпангоутными линиями переносят на соответствующие проекции шпангоутов плазового корпуса, измеряя отрезки от пазовых кромок до точек пересечения диагоналей со шпангоутами. На плазовом корпусе диагонали изображаются кривыми линиями. Растяжки проекций диагоналей строят обычным путём. Если длина полученных растяжек диагоналей будет соответствовать длине прямых диагоналей развёрнутого листа, то можно быть уверенным в правильности построения контура листа обшивки. |