построение теоретического чертежа корпуса судна. Г. Текст. Волжская государственная академия водного транспорта
 Скачать 3.07 Mb. Скачать 3.07 Mb.
|
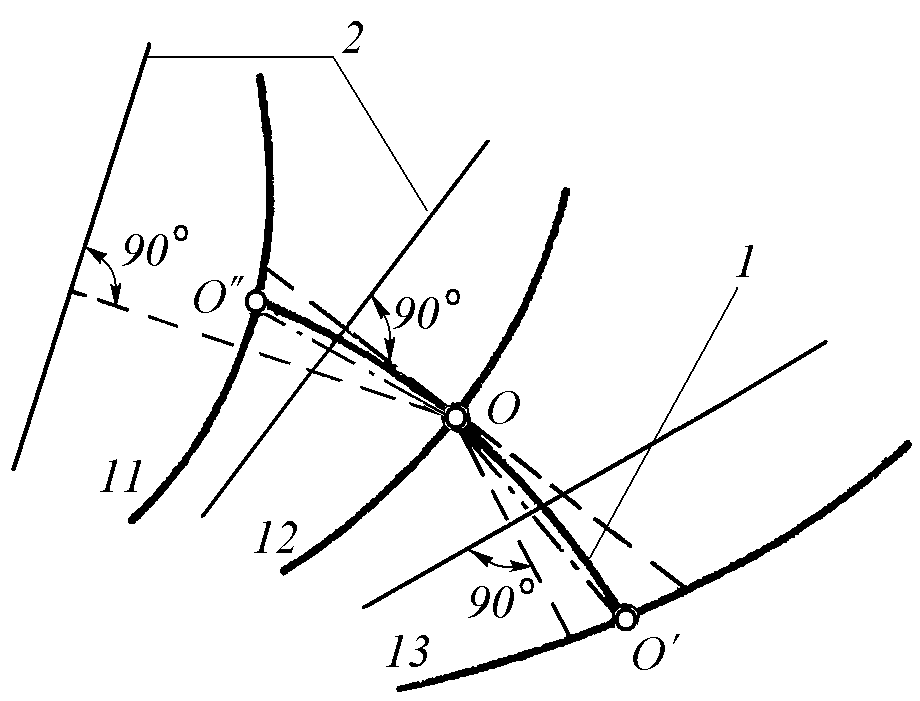
2.4.6. Американский способ (рис. 2.16) применяют при плавном изменении кривизны шпангоутов на проекции листа. Он более прост, но позволяет достаточно точно построить среднюю нормаль.
На плазовом корпусе проводят хорды шпангоутных дуг, ограниченных контурами листа. На среднем шпангоуте (шп. 12) выбирают точку О, приходящуюся на вершину погиби, и из неё опускают перпендикуляры на хорды 13-го и 11-го шпангоутов. Углы между этими перпендикулярами и перпендикуляром к точке О делят пополам и проводят биссектрисы до пересечения с дугами 13-го и 11-го шпангоутов. Полученные точки О' и О" служат началом подобного же построения.
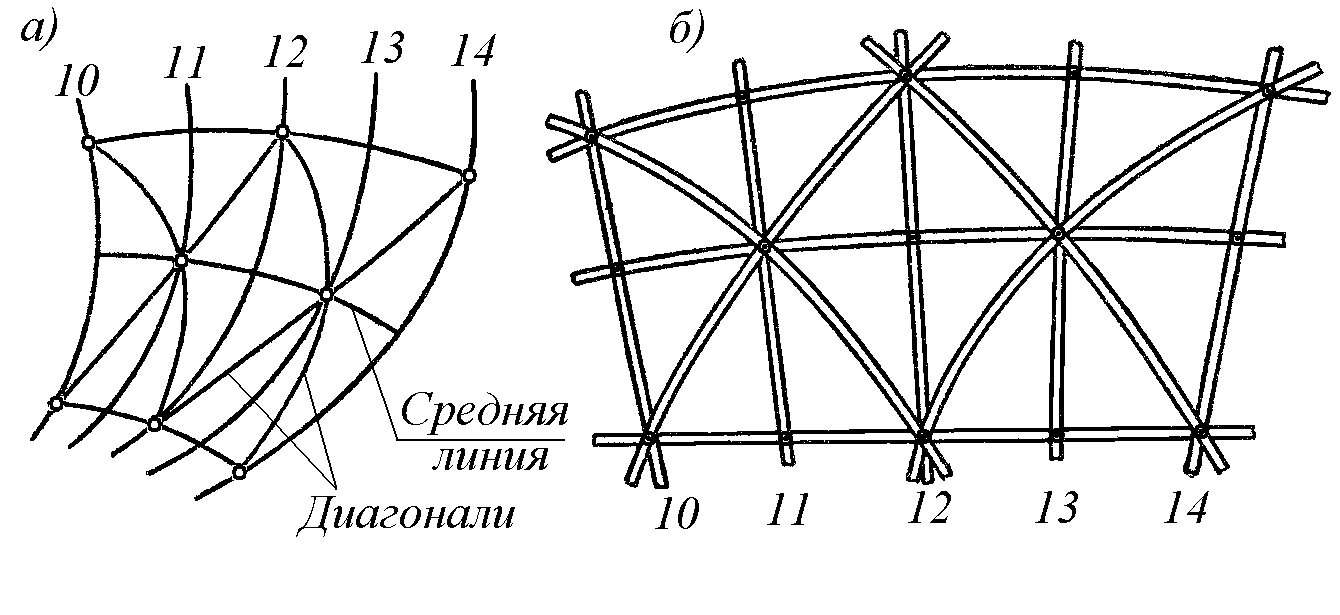
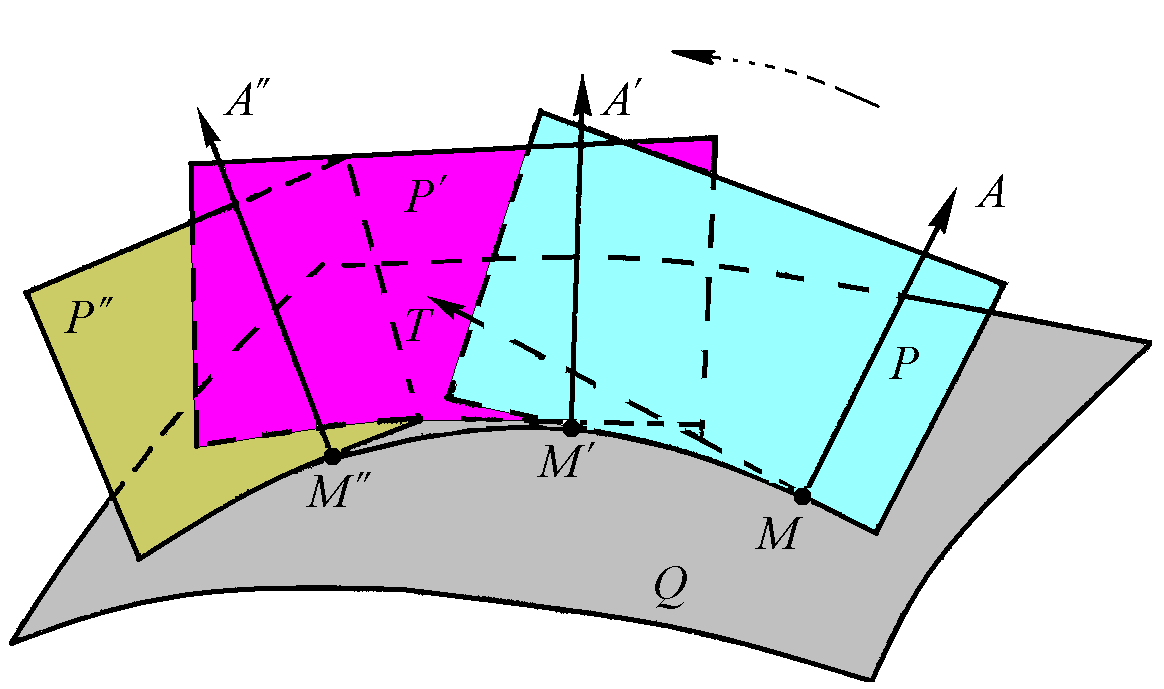
2.4.7. Развёртывание листов может быть выполнено и без построения строевой, например, при помощи диагональных линий (метод диагоналей). При этом методе (его так же называют голландским методом) на проекции листа на плазовом корпусе наносят среднюю линию и проекции диагоналей в двух смежных шпациях (рис. 2.17, а). Затем выполняют растяжки всех линий, по ним заготовляют деревянные рейки, из которых сколачивают шаблон листа, развёрнутого на плоскость (рис. 2.17, б). Способ прост, однако недостаточно точен и весьма трудоёмок. 2.4.8. Для масштабного плаза разработан способ развёртывания листов сложной кривизны, в котором в качестве строевой принята геодезическая линия. Геодезической линией данной поверхности называется такая линия, соприкасающаяся плоскость которой в любой точке линии перпендикулярна касательной плоскости этой поверхности в этой же точке. Характерным свойством геодезической линии является то, что она при спрямлении развёртываемой поверхности становится прямой. Соприкасающейся плоскостью пространственной кривой называется такая плоскость, которая проходит через три бесконечно близкие точки этой кривой. Геодезическая линия соединяет точки поверхности в заданном направлении по кратчайшему расстоянию. .1 Геодезическая линия на произвольной поверхности строится следующим образом. На поверхности Q (см. рис. 2.18) выбирают начальную точку М и направление геодезической линии в этой точке, то есть прямую МТ. Через прямую МТ и нормаль к поверхности МА проводят плоскость Р. Эта плоскость пересекает поверхность Q по кривой лини.
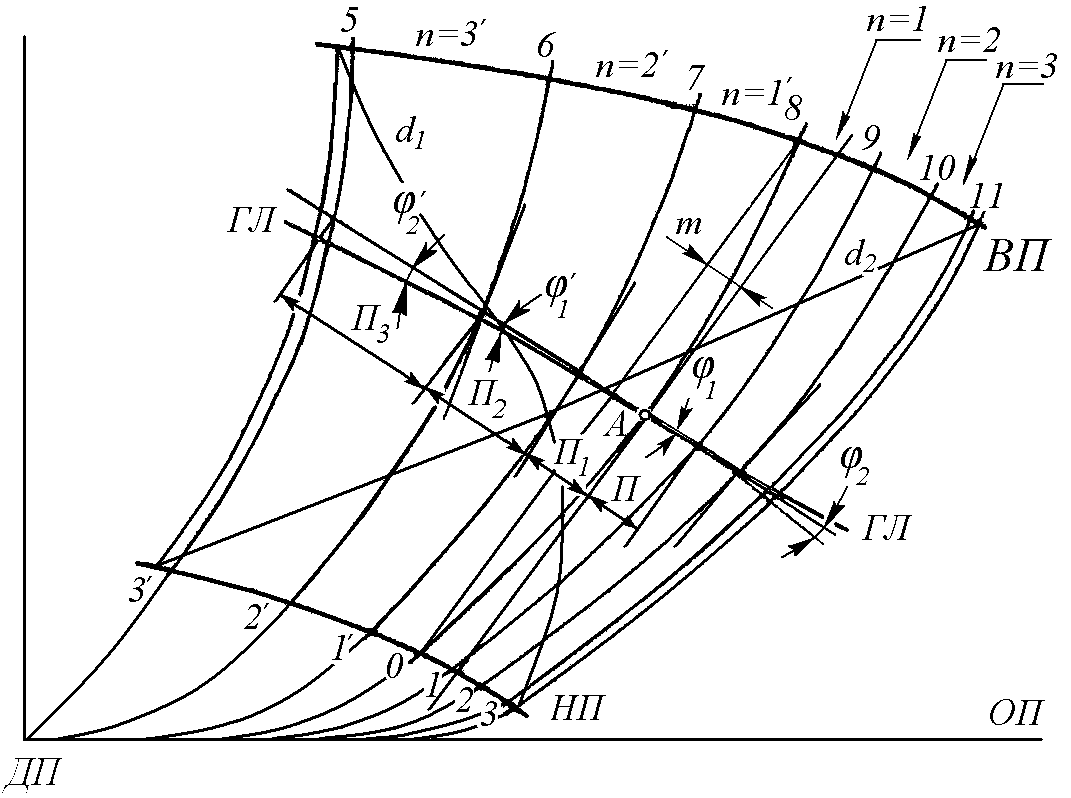
На линии пересечения откладывают дугу ММ′. В точке М′ строят нормаль к поверхности М′А′. Через эту нормаль и точку М′ проводят плоскость Р′. На линии пересечения поверхности этой плоскостью откладывают дугу М′М′′. В точке М′′ строят нормаль к поверхности М′′А′′. Через нормаль М′′А′′ и точку М′′ проводят плоскость Р′′ и т. д. Построенная таким образом линия приближается к геодезической и в пределе, при стремлении этих дуг к нулю, она становится геодезической линией. .2 Лист, подлежащий развёртыванию на плоскость, задаётся частью практического корпуса судна, ограниченной верхним (ВП) и нижним (НП) пазами, шпангоутами в пределах этого листа и линиями кормового и носового стыков (рис. 2.19). Все графические построения и расчёты выполняются в том масштабе, в каком выполнена проекция листа на корпусе.
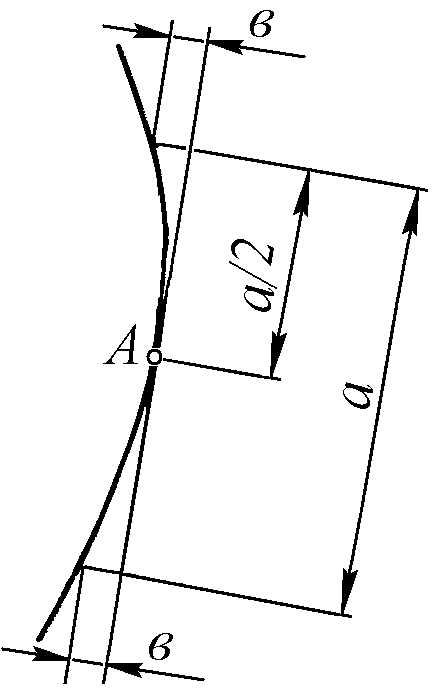
3. Построение геодезической линии на проекции листа заключается в следующем. Выбирается средний (начальный) шпангоут в пределах развёртываемого листа и проводится хорда, стягивающая пазовые точки этого шпангоута. Проводится касательная к среднему шпангоуту параллельно хорде. Если лист ограничен чётным числом шпангоутов; то построение начинается от одного из средних шпангоутов, лучше с того, который имеет большую кривизну. Определяется точка касания. Для этого на касательной находят точки, одинаково удалённые от шпангоута (на 1–2 мм), а расстояние Q делится пополам (рис. 2.20). Полученная точка А считается точкой касания. Через точку А проводят нормаль к начальному шпангоуту и продолжают её в обе стороны до пересечения со всеми шпангоутами. Затем строятся нормали к каждому из остальных шпангоутов (кроме крайних) через точки пересечения их с нормалью к начальному шпангоуту. Определяются углы φ между нормалями к смежным шпангоутам. Точка А (см. рис. 2.20) определяет начало геодезической линии на проекции листа, а нормаль к начальному шпангоуту её направление в районе этого шпангоута. Положение геодезической лини на шпангоутах, смежных с начальным, определяется точками пересечения их с нормалью к начальному шпангоуту. Положение геодезической линии на всех остальных шпангоутах определяется отклонением от нормали к начальному шпангоуту, которое может быть рассчитано по формуле:
где ∆i – смещение геодезической линии от нормали к начальному шпангоуту по i-ому шпангоуту, мм; i – условный порядковый номер шпангоута (у начального шпангоута i=0); n – порядковый номер шпации в направлении от начального шпангоута); Пn, Пn+1 – прогрессы шпаций, измеренные в направлении нормали к начальному шпангоуту, соответственно для шпаций n и n+1, мм; k – коэффициент, определяемый по формуле k=i-n; в расчёт принимаются только положительные значения k. φ – угол между нормалью к начальному шпангоуту и нормалью к i-ому шпангоуту, рад. 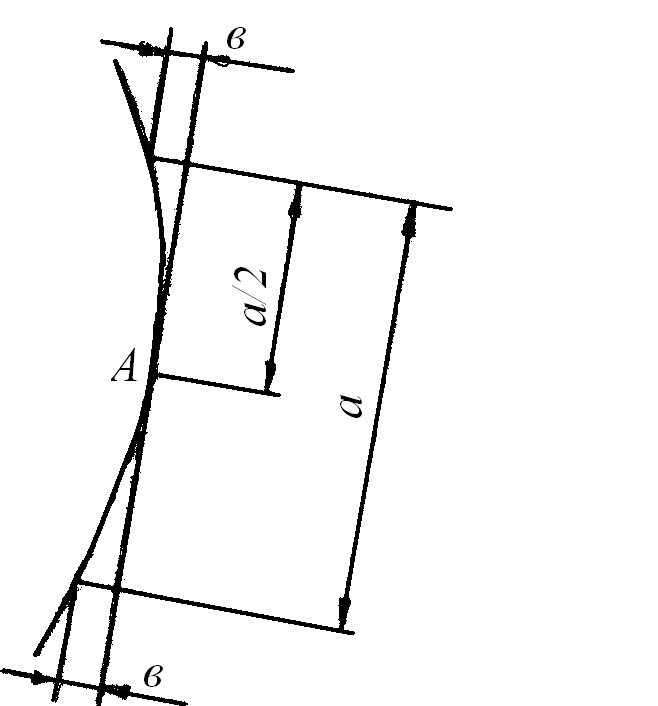 Рис.5.2 Определение точки касания Угол φi должен быть определён в радианах. При использовании транспортира шкала которого нанесена в градусах, необходимо произвести пересчёт замеренного угла по формуле:
где φр – угол φi, определяемый в радианах; φº – угол φi, измеренный в градусах. Смещение геодезической линии по формуле (2.1) определяют в табличной форме (табл. 2.1). Первый столбец таблицы содержит условный номер шпации n. Нумерация шпаций начинается от начального шпангоута. Второй столбец заполняется номерами шпангоутов, которые ограничивают соответствующую шпацию. Третий, четвертый, пятый и шестой столбцы заполняются значениями прогрессов, разностями прогрессов, углов между нормалями и произведениями (Пn+1-Пn)·φi. При этом знаки углов и разности прогрессов не учитываются. В седьмом и всех последующих столбцах производят вычисления смещений геодезической линии. Седьмой и последующие нечётные столбцы заполняются значениями коэффициентов k=i-n (только нулевые и положительные значения). Таблица 2.1. |