Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр

• Название: Задачи теории игр в экономике, финансах и бизнесе. Теория игр
• Анкор: Теория игр - теоретический материал, все вопросы.docx
• Дата: 02.05.2017
• Размер: 4.21 Mb.
• Имя файла: Теория игр - теоретический материал, все вопросы.docx
• Тип: Документы; #6343
• Категория: Математика
• страница: 19 из 27

Критерий Ходжа – Лемана оптимальности чистых стратегий относительно выигрышей.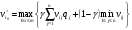

матрица выигрышей

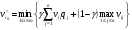матрица потерь
y- параметр отражающий степень доверия ЛПР к оценкам вероятностей состояния природы.

y 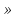[0,1]

Чем выше у, тем выше доверие игрока А к оценкам вероятности. А следовательно от того как У зависит доминирует первое слагаемое или второе.

Критерий Ходжа-Лемана

1) Предположим, что матрицей выигрышей игрока А является матрица А.

2) Известны вероятности q_i=p(П_j), j=1,…,n, состояний природы П_j, j=1,…,n, удовлетворяющие условию (1).

Таким образом, игроку А надлежит принимать решение в условиях риска.

3) Пусть l=2,

(11)

• 
  показатель эффективности стратегии А_i по критерию Вальда,
  

(12)

• 
  показатель эффективности стратегии А_i по критерию Байеса.
  

Матрица В примет вид

В=

т.е. b_i1=W_i, b_i2=B_i, i=1,…,m.

4) Коэффициенты l₁, l₂ выбираются следующим образом:

l1=1-l,    l2=l, где lÎ[0, 1].

(13)

Очевидно, что эти коэффициенты удовлетворяют условию (2).

5) По формуле (3), с учетом (11), (12), и (13), показатель эффективности стратегии А_i по критерию Ходжа-Лемана равен:

Gi=libi1+l2bi2=(1-l)Wi+lBi=(1-l)aij+l qiaj i=1,…,m.	(14)

В правой части формулы (14) коэффициент lÎ[0, 1] есть количественный показатель степени доверия игрока А данному распределению вероятностей q_i=p(П_j), j=1,…,n, состояний природы П_j, j=1,…,n, а коэффициент (1-l) характеризует количественно степень пессимизма игрока А. Чем больше доверия игрока А данному распределению вероятностей состояний природы, тем меньше пессимизма и наоборот.

6) Цену игры по критерию Ходжа-Лемана находим по формуле (4):

7) Оптимальной стратегией по критерию Ходжа-Лемана является стратегия А_k с наибольшим показателем эффективности:

G_k=G.

Отметим, что критерий Ходжа-Лемана является как-бы промежуточным критерием между критериями Байеса и Вальда. При l=1, из (14) имеем:G_i=B_i и потому критерий Ходжа-Лемана превращается в критерий Байеса. А при l=0, из (14): G_i=W_i и, следовательно, из критерия Ходжа-Лемана получаем критерий Вальда.

Пример.

Исходная матрица

	q=0,4 П1	q=0,3 П2	q=0,1 П3	q=0,2 П4
S1	6	3	4	5
S2	4	3	6	5

Далее используя формулы –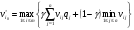

матрица выигрышей

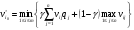матрица потерь

каждый элемент в столбце на соответствующий коэффициент q. Получим следующую таблицу :

Vi1*q1		Vi2*q2		Vi3*q3		Vi4*q4
2,4	0,9		0,8		0,5		4,6
1,6	0,9		1,2		0,5		4,2

Принимая 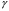=0,6

Получим итоговые данные, для выйгрыша выберем макс. Элемент, для потерь – мин.

HL(выйгрыш)	HL (потеря)
4,02	5,22
3,66	4,86

Получаем следующий ответ : S^*=S₁ , V^*=4,02 - выигрыш

S^*=S₂ , V^*=4,86 - потеря