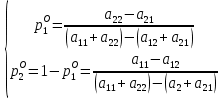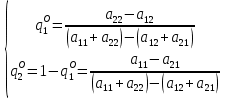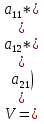Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
Равновесие по Нэшу в чистых стратегиях.Набор стратегий s=(s1, … , sn) образует равновесие по Нэшу если для любого Pk, (или ситуация s=(s1, … , sn) является равновесной по Нэшу) |
| | B1 | B2 |
| A1 | a11 | a12 |
| А2 | a21 | a22 |
А=
Сначала предположим, что матрица А имеет седловую точку aij, то есть элемент aij, наименьший в i-той строке и наибольший в j-том столбце. Тогда игра имеет решение в чистых стратегиях {Ai, Bj, V=aij}, где Ai и Bj- оптимальные стратегии соответственно игроков A и B, а V=aij – цена игры.
Рассмотрим случай, когда матрица [2x2]-не имеет седловой точки.
Тогда по теореме, каждый из игроков A и B обладает единственной оптимальной смешанной стратегией соответственно PO=(p1O,p2O) и QO=(q1O,q2O), где
а цена игры (в смешанных стратегиях) V определяется формулой
Пояснение (без строгого доказательства):
Рассмотрим функцию выигрыша игрока A более подробно:
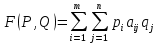 ,
, 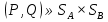 .
.Примем также следующие обозначения:
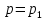 ,
, 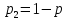 ,
,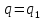 ,
, 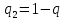 .
.Пусть
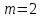 и
и 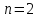 , тогда функцию
, тогда функцию 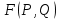 можно переписать в виде:
можно переписать в виде: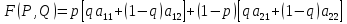 .
.Представим в явном виде функцию
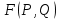 как линейную функцию с аргументом (независимой переменной) q. Получим следующее выражение:
как линейную функцию с аргументом (независимой переменной) q. Получим следующее выражение: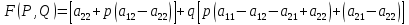 .
.Если
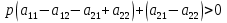 , т.е. если
, т.е. если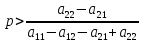 , график функции имеет положительный наклон. Это значит, что в ответ на действия игрока A игрок B будем минимизировать свои потери (минимизировать функцию
, график функции имеет положительный наклон. Это значит, что в ответ на действия игрока A игрок B будем минимизировать свои потери (минимизировать функцию 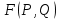 ), выбирая свою второю чистую стратегию, т.е. реализуя смешанную стратегию
), выбирая свою второю чистую стратегию, т.е. реализуя смешанную стратегию 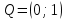 ,
, 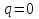 . В итоге исход игры определится результатом
. В итоге исход игры определится результатом 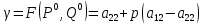 .
.Если
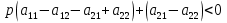 , т.е. если
, т.е. если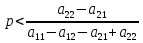 , график функции имеет отрицательный наклон. Это значит, что в ответ на действия игрока A игрок B будем минимизировать функцию
, график функции имеет отрицательный наклон. Это значит, что в ответ на действия игрока A игрок B будем минимизировать функцию 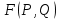 , выбирая свою первую чистую стратегию
, выбирая свою первую чистую стратегию 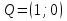 ,
, 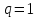 .
.В итоге исход игры определится результатом
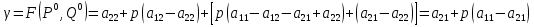 .
.В итоге приходим к системе, решая которую, получим формулы, представленные в утверждении теоремы.
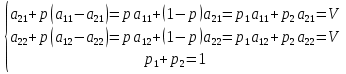

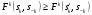
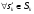
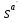 s
s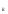 - альтернатива стратегии a-ого игрока
- альтернатива стратегии a-ого игрока 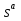
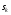 ,
, 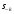 - игровая ситуация, которая сложилась в результате выбора своих стратегий всеми игроками кроме a-ого
- игровая ситуация, которая сложилась в результате выбора своих стратегий всеми игроками кроме a-ого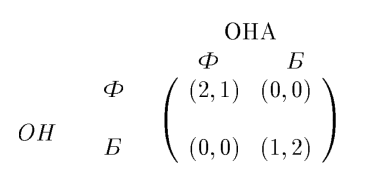
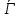 ={А, {Σa}, {
={А, {Σa}, {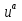 }}, если для любого а=1, …, n
}}, если для любого а=1, …, n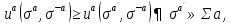
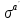 - альтернатива стратегии a-ого игрока
- альтернатива стратегии a-ого игрока 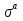 ,
, 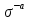 - игровая ситуация, которая сложилась в результате выбора своих стратегий всеми игроками кроме a-ого.
- игровая ситуация, которая сложилась в результате выбора своих стратегий всеми игроками кроме a-ого.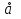 Sa – множество чистых стратегий, которые игрок a играет с положительной вероятностью в ситуации σ=( σ1, … , σn). Ситуация σ является равновесной по Нэшу в смешанном расширении
Sa – множество чистых стратегий, которые игрок a играет с положительной вероятностью в ситуации σ=( σ1, … , σn). Ситуация σ является равновесной по Нэшу в смешанном расширении 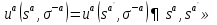 Sa+
Sa+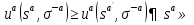 Sa+,
Sa+, 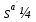 Sa+
Sa+